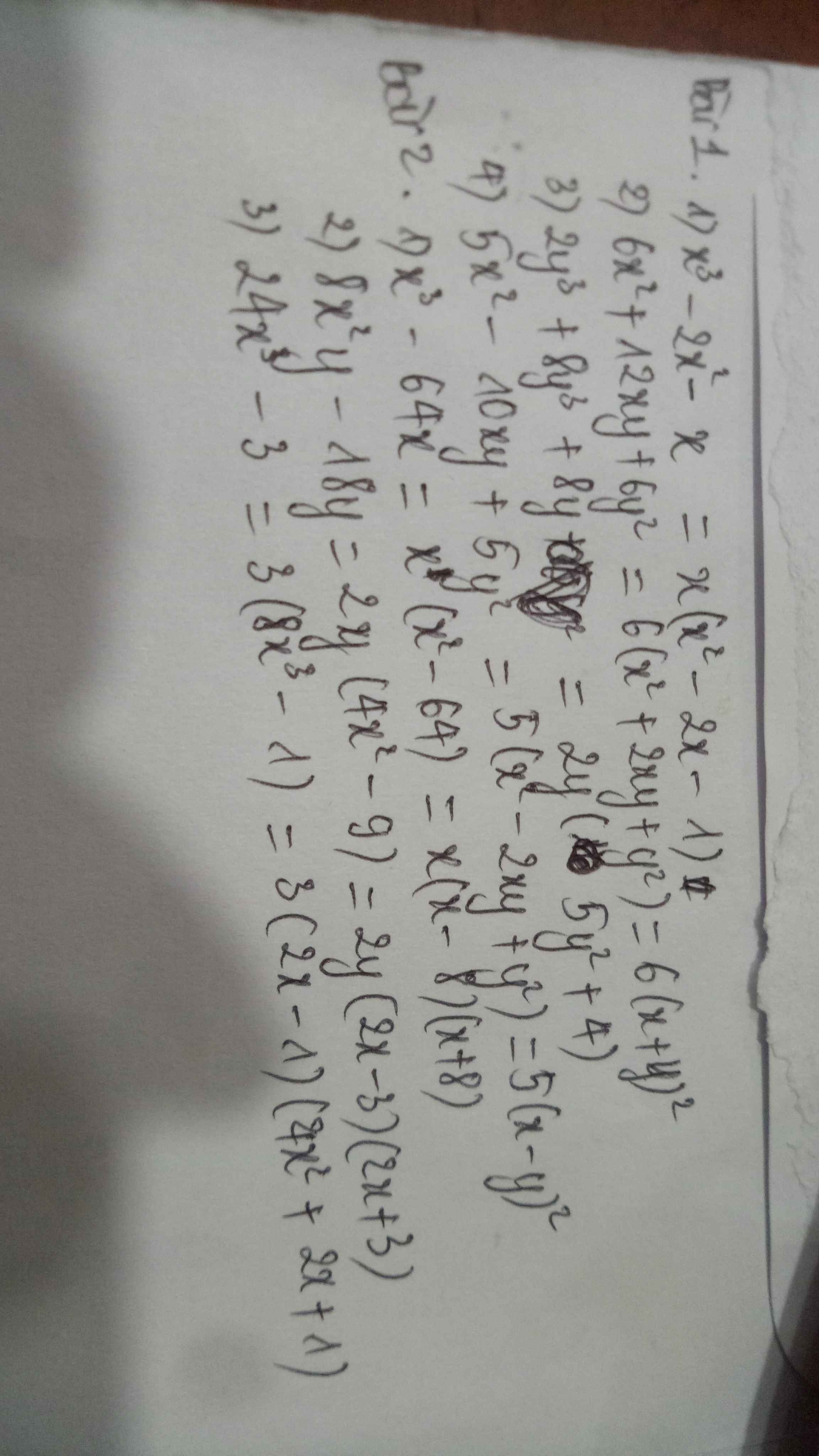(12x^2 - 12xy + 3y^2) - 10.(2x - y) + 8 

= 3(4x^2 - 4xy + y^2) - 10(2x - y) + 8 

= 3(2x - y)^2 - 10(2x - y) + 8 

= 3(2x - y)^2 - 10(2x - y) + 8 

= 3(2x - y)^2 - 6(2x - y) - 4(2x - y) + 8 

= 3(2x - y)(2x - y - 2) - 4(2x - y -2) 

= (2x - y -2)[3(2x - y) - 4] 

= (2x - y -2)(6x - 3y -4)

Ai k mk mk k lại

(12x^2 - 12xy + 3y^2) - 10.(2x - y) + 8 
= 3(4x^2 - 4xy + y^2) - 10(2x - y) + 8 
= 3(2x - y)^2 - 10(2x - y) + 8 
= 3(2x - y)^2 - 10(2x - y) + 8 
= 3(2x - y)^2 - 6(2x - y) - 4(2x - y) + 8 
= 3(2x - y)(2x - y - 2) - 4(2x - y -2) 
= (2x - y -2)[3(2x - y) - 4] 
= (2x - y -2)(6x - 3y -4)

3*(\(4x^2-4xy+y^2\))-10(2x-y)+8

3*(2x-y)^2-10(2x-y)+8

3*(2x-y)^2-6(2x-y)-4(2x-y)+8

3(2x-y)(2x-y-2)-4(2x-y-2)

(2x-y-2)(6x-3y-40

\(\left(12x^2-12xy+3y^2\right)-10\left(2x-y\right)+8\)

\(=\left(12x^2-6xy-6xy+3y^2\right)-10\left(2x-y\right)+8\)

\(=\left[6x\left(2x-y\right)-3y\left(2x-y\right)\right]-10\left(2x-y\right)+8\)

\(=\left(2x-y\right)\left(6x-3y\right)-10\left(2x-y\right)+8\)

\(=3\left(2x-y\right)^2-10\left(2x-y\right)+8\)

Đặt \(2x-y=a\), khi đó biểu thức có dạng:

\(3a^2-10a+8=3a^2-6a-4a+8\)

\(=3a\left(a-2\right)-4\left(a-2\right)=\left(a-2\right)\left(3a-4\right)\)

\(=\left(2x-y-2\right)\left(6x-3y-4\right).\)

a) \(A=x^2-2xy+y^2+3x-3y-4\)

\(=\left(x-y\right)^2-1+3x-3y-3\)

\(=\left(x-y-1\right)\left(x-y+1\right)+3\left(x-y-1\right)\)

\(=\left(x-y-1\right)\left(x-y+1+3\right)\)

\(=\left(x-y-1\right)\left(x-y+4\right)\)

6) \(9x^3y^2+3x^2y^2=3x^2y^2\left(3x+1\right)\)

7) \(x^3+2x^2+3x=x\left(x^2+2x+3\right)\)

8) \(6x^2y+4xy^2+2xy=2xy\left(3x+2y+1\right)\)

9) \(5x^2\left(x-2y\right)-15x\left(x-2y\right)=5x\left(x-2y\right)\left(x-3\right)\)

10) \(3\left(x-y\right)-5x\left(y-x\right)=\left(x-y\right)\left(3+5x\right)\)

6) 9x³y² + 3x²y² = 3x²y²( 3x + 1 )

7) x³ + 2x² + 3x = x( x² + 2x + 3 )

8) 6x²y + 4xy² + 2xy = 2xy( 3x + 2y + 1 )

9) 5x²( x - 2y ) - 15x( x - 2y ) = 5x( x - 2y )( x - 3 )

10 3( x - y ) - 5x( y - x ) = 3( x - y ) + 5x( x - y ) = ( x - y )( 3 + 5x )

a, \(9x^3y^2+3x^2y^2=3x^2y^2\left(3x+1\right)\)

b, \(x^3+2x^2+3x=x\left(x^2+2x+3\right)\)

c, \(6x^2y+4xy^2+2xy=2xy\left(3x+2y+1\right)\)

d, \(5x^2\left(x-2y\right)-15x\left(x-2y\right)=\left(5x^2-15x\right)\left(x-2y\right)=5x\left(x-3\right)\left(x-2y\right)\)

e, \(3\left(x-y\right)-5x\left(y-x\right)=3\left(x-y\right)+5x\left(x-y\right)=\left(3+5x\right)\left(x-y\right)\)

\(\left(x^2+4x+8\right)^2+3x\left(x^2+4x+8\right)+2x^2=\left(x^2+4x+8+\dfrac{3}{2}x\right)^2-\dfrac{1}{4}x^2=\left(x^2+\dfrac{11}{2}x+8\right)^2-\left(\dfrac{1}{2}x\right)^2=\left(x^2+\dfrac{11}{2}x+8-\dfrac{1}{2}x\right)\left(x^2+\dfrac{11}{2}x+8+\dfrac{1}{2}x\right)=\left(x^2+5x+8\right)\left(x^2+6x+8\right)=\left(x+2\right)\left(x+4\right)\left(x^2+5x+8\right)\)

\(\left(x^2+4x+8\right)^2+3x\left(x^2+4x+8\right)+2x^2\)

\(=\left(x^2+4x+8\right)^2+x\left(x^2+4x+8\right)+2x\left(x^2+4x+8\right)+2x^2\)

\(=\left(x^2+4x+8\right)\left(x^2+5x+8\right)+2x\left(x^2+5x+8\right)\)

\(=\left(x^2+5x+8\right)\left(x+2\right)\left(x+4\right)\)

\(9\left(x-3y\right)^2-25\left(2x+y\right)^2\)

\(=\left[3\left(x-3y\right)\right]^2-\left[5\left(2x+y\right)\right]^2\)

\(=\left(3x-9y\right)^2-\left(10x+5y\right)^2\)

\(=\left[3x-9y+10x+5y\right]\left[3x-9y-\left(10x+5y\right)\right]\)

\(=\left(13x-4y\right)\left(-7x-14y\right)\)

\(=-7\left(x+2y\right)\left(13x-4y\right)\)

9(x - 3y)² - 25(2x + y)²

= 3².(x - 3y)² - 5².(2x + y)²

= (3x - 9y)² - (10x + 5y)²

= (3x - 9y - 10x - 5y)(3x - 9y + 10x + 5y)

= (-7x - 14y)(13x - 4y)

= -7(x + 2y)(13x - 4y)

Bài 1:

\(1,Sửa:x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)

Bài 2:

\(1,=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\\ 2,=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\\ 3,=3\left(x^3-1\right)=3\left(x-1\right)\left(x^2+x+1\right)\)

Bài 3:

\(a,=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y^2\right]=5\left(x-y+1\right)\left(x+y+1\right)\\ b,=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-4y^2\right]\\ =3x\left(x-2y-1\right)\left(x+2y-1\right)\\ c,=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\\ =\left(a+b\right)\left(a^2b-ab^2+a+b\right)\\ d,=2x\left(x^2-y^2-4x+4\right)=2x\left[\left(x-2\right)^2-y^2\right]\\ =2x\left(x-y-2\right)\left(x+y-2\right)\)

Bài 1;

1) \(x^3-2x-x=x\left(x^2-2x-1\right)\)

2) \(6x^2+12xy+6y^2=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\)

3) \(2y^3+8y^3+8y=10y^3+8y=2y\left(5y^2+4\right)\)

4) \(5x^2-10xy+5y^2=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)

Bài 2:

1) \(x^3-64x=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\)

2) \(8x^2y-18y=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\)

3) \(24x^3-3=3\left(8x^3-1\right)=3\left(2x-1\right)\left(4x^2+2x+1\right)\)

Bài 3:

1) \(5x^2+10x+5-5y^2=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y\right]=5\left(x-y+1\right)\left(x+y+1\right)\)

2) \(3x^3-6x^2+3x-12xy^2=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-\left(2y\right)^2\right]=3x\left(x-2y-1\right)\left(x+2y-1\right)\)

3) \(a^3b-ab^3+a^2+2ab+b^2=ab\left(a^2-b^2\right)+\left(a+b\right)^2=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2=\left(a+b\right)\left(a^2b-ab^2+a+b\right)\)

4) \(2x^3-2xy^2-8x^2+8xy=2x\left(x^2-y^2-4x+4y\right)=2x\left[\left(x-y\right)\left(x+y\right)-4\left(x-y\right)\right]=2x\left(x-y\right)\left(x+y-4\right)\)