\(2x;2x-1;4x^2-2x=2x\left(2x-1\right)\)

\(MTC=2x\left(2x-1\right)\)

\(\dfrac{1-3x}{2x}+\dfrac{3x-2}{2x-1}+\dfrac{2-3x}{4x^2-2x}\)

\(=\dfrac{\left(1-3x\right).2x\left(2x-1\right)}{2x\left(2x-1\right)}+\dfrac{\left(3x-2\right).2x}{\left(2x-1\right).2x}+\dfrac{2-3x}{2x\left(2x-1\right)}\)

\(=\dfrac{2x\left(1-3x\right)\left(2x-1\right)+2x\left(2x-2\right)+2-3x}{2x\left(2x-1\right)}\)

\(=\dfrac{-8x^2+4x+4x^2-4x+2-3x}{2x\left(2x-1\right)}\)

\(=\dfrac{-4x^2-3x+2}{2x\left(2x-1\right)}\)

#AEZn8

\(\dfrac{1-3x}{2x}+\dfrac{3x-2}{2x-1}+\dfrac{2-3x}{4x^2-2x}=\dfrac{\left(1-3x\right)\left(2x-1\right)}{2x\left(2x-1\right)}+\dfrac{2x\left(3x-2\right)}{2x\left(2x-1\right)}+\dfrac{2-3x}{2x\left(2x-1\right)}=\dfrac{-6x^2+5x-1}{2x\left(2x-1\right)}+\dfrac{6x^2-4x}{2x\left(2x-1\right)}+\dfrac{2-3x}{2x\left(2x-1\right)}=\dfrac{\left(-6x^2+6x^2\right)+\left(5x-4x-3x\right)+\left(-1+2\right)}{2x\left(2x-1\right)}=\dfrac{-2x}{2x\left(2x-1\right)}=\dfrac{-1}{2x-1}\)

1)  (2x + 1)(3x – 2) = (5x – 8)(2x + 1)

⇔ (2x + 1)(3x – 2) – (5x – 8)(2x + 1) = 0

⇔ (2x + 1).[(3x – 2) – (5x – 8)] = 0

⇔ (2x + 1).(3x – 2 – 5x + 8) = 0

⇔ (2x + 1)(6 – 2x) = 0

⇔\(\left[{}\begin{matrix}2x+1=0\\6-2x=0\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=\dfrac{-1}{2}\\x=3\end{matrix}\right.\)

Vậy.....

2)  4x² -1 = (2x + 1)(3x - 5)

⇔ (2x-1)(2x+1)-(2x+1)(3x-5)=0

⇔ (2x+1)(2x-1-3x+5)=0

⇔ (2x+1)(4-x)=0

⇔ \(\left[{}\begin{matrix}2x+1=0\\4-x=0\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=\dfrac{-1}{2}\\x=4\end{matrix}\right.\)

Vậy...

3)  

(x + 1)² = 4(x² – 2x + 1)

⇔ (x + 1)² - 4(x² – 2x + 1) = 0

⇔ x² + 2x +1- 4x² + 8x – 4 = 0

⇔ - 3x² + 10x – 3 = 0

⇔ (- 3x² + 9x) + (x – 3) = 0

⇔ -3x (x – 3)+ ( x- 3) = 0

⇔ ( x- 3) ( - 3x + 1) = 0

⇔\(\left[{}\begin{matrix}x-3=0\\-3x+1=0\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x=3\\x=\dfrac{1}{3}\end{matrix}\right.\)

Vậy......

4) 2x³+5x²-3x=0

⇒2x³-x²+6x²-3x=0

⇒(2x³-x²)+(6x²-3x)=0

⇒x²(2x-1)+3x(2x-1)=0

⇒(x²+3x)(2x-1)=0

⇒ hoặc x²+3x=0⇒x(x+3)=0⇒hoặc x=0 hoặc x=-3

hoặc 2x-1=0⇒x=0,5

Vậy ...

5)2x=3x-2

⇒2x-3x=-2

⇒-x=-2

⇒x=2

6) x+15=3x-1

⇒x-3x=-1-15

⇒-2x=-16

⇒x=8

7)2-x=0,5x-4

⇒-x-0,5x=-4-2

⇒-1,5x=-6

⇒x=4

1) Ta có: \(2x\left(x-3\right)+5\left(x-3\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)

2) Ta có: \(\left(x^2-4\right)-\left(x-2\right)\left(3-2x\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+2\right)+\left(x-2\right)\left(2x-3\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(3x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)

3) Ta có: \(\left(2x-1\right)^2-\left(2x+5\right)^2=11\)

\(\Leftrightarrow4x^2-4x-1-4x^2-20x-25=11\)

\(\Leftrightarrow-24x=11+1+25=37\)

hay \(x=-\dfrac{37}{24}\)

5) Ta có: \(3x^2-5x-8=0\)

\(\Leftrightarrow3x^2+3x-8x-8=0\)

\(\Leftrightarrow3x\left(x+1\right)-8\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(3x-8\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{8}{3}\end{matrix}\right.\)

8) Ta có: \(\left|x-5\right|=3\)

\(\Leftrightarrow\left[{}\begin{matrix}x-5=3\\x-5=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=2\end{matrix}\right.\)

10) Ta có: \(\left|2x+1\right|=\left|x-1\right|\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=x-1\\2x+1=1-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=-1-1\\2x+x=1-1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=0\end{matrix}\right.\)

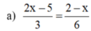
⇔ 4x - 10 = 2 - x

⇔ 4x + x = 2 + 10 ⇔ 5x = 12 ⇔ x = 12/5

Vậy: S = {12/5}

b) (3x + 1) = (3x + 1)2

⇔ (3x + 1)2 - (3x + 1) = 0

⇔ (3x + 1)[(3x + 1) - 1] = 0

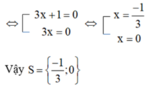
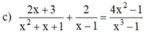
ĐKXĐ:x ≠ 1

Quy đồng mẫu hai vế của phương trình ta được:

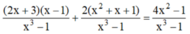
Khử mẫu hai vế, ta được:

(2x + 3)(x - 1) + 2(x2 + x + 1) = 4x2 - 1

⇔ 2x2 + x - 3 + 2x2 + 2x + 2 = 4x2 - 1

⇔ 3x - 1 = -1

⇔ 3x = 0 ⇔ x = 0 (thỏa mãn điều kiện)

Vậy: S = {0}

\(\dfrac{x+10}{x-2}+\dfrac{x-18}{x+2}+\dfrac{x+2}{x^2-4}=\dfrac{\left(x+10\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{\left(x-18\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+12x+20+x^2-16x-36+x+2}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x^2-3x-14}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(2x^2+4x\right)-\left(7x+14\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x\left(x+2\right)-7\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(2x-7\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x-7}{x-2}\)

\(\dfrac{3-3x}{2x}+\dfrac{3x-1}{2x-1}+\dfrac{11x-5}{2x-4x^2}\\ =\dfrac{\left(3-3x\right)\left(1-2x\right)}{2x\left(1-2x\right)}-\dfrac{2x\left(3x-1\right)}{2x\left(1-2x\right)}+\dfrac{11x-5}{2x\left(1-2x\right)}\\ =\dfrac{3-9x+6x^2}{2x\left(1-2x\right)}-\dfrac{6x^2-2x}{2x\left(1-2x\right)}+\dfrac{11x-5}{2x\left(1-2x\right)}\\ =\dfrac{3-9x+6x^2-6x^2+2x+11x-5}{2x\left(1-2x\right)}\\ =\dfrac{-2}{2x\left(1-2x\right)}\\ =\dfrac{-1}{x\left(1-2x\right)}\)

\(a,\left(3x-7\right)^2=\left(2-2x\right)^2\)

a,\(=>\left(3x-7\right)^2-\left(2-2x\right)^2=0\)

\(< =>\left(3x-7+2-2x\right)\left(3x-7-2+2x\right)=0\)

\(< =>\left(x-5\right)\left(5x-9\right)=0=>\left[{}\begin{matrix}x=5\\x=1,8\end{matrix}\right.\)

b, \(x^2-8x+6=0< =>x^2-2.4x+16-10=0\)

\(< =>\left(x-4\right)^2-\sqrt{10}^2=0\)

\(=>\left(x-4+\sqrt{10}\right)\left(x-4-\sqrt{10}\right)=0\)

\(=>\left[{}\begin{matrix}x=4-\sqrt{10}\\x=4+\sqrt{10}\end{matrix}\right.\)

c, \(4x^2-2x-1=0\)

\(< =>\left(2x\right)^2-2.2.\dfrac{1}{2}x+\dfrac{1}{4}-\dfrac{5}{4}=0\)

\(=>\left(2x-\dfrac{1}{2}\right)^2-\left(\dfrac{\sqrt{5}}{2}\right)^2=0\)

\(=>\left(2x+\dfrac{-1+\sqrt{5}}{2}\right)\left(2x-\dfrac{1+\sqrt{5}}{2}\right)=0\)

\(=>\left[{}\begin{matrix}x=\dfrac{1-\sqrt{5}}{4}\\x=\dfrac{1+\sqrt{5}}{4}\end{matrix}\right.\)

d,\(x^4-4x^2-32=0\)

đặt \(t=x^2\left(t\ge0\right)=>t^2-4t-32=0\)

\(< =>t^2-2.2t+4-6^2=0\)

\(=>\left(t-2\right)^2-6^2=0=>\left(t-8\right)\left(t+4\right)=0\)

\(=>\left[{}\begin{matrix}t=8\left(tm\right)\\t=-4\left(loai\right)\end{matrix}\right.\)\(=>x=\pm\sqrt{8}\)

\(a,=9x^2+12x+4-18x-4+10x^2=19x^2-6x\\ b,=8x^3-27-8x^3-36x^2-54x-27=-36x^2-54x-54\)

\(a,=6x^2-4x-x^2-4x-4=5x^2-8x-4\\ b,=x^3+8-2\left(1-x^2\right)=x^3+8-2+2x^2=x^3+2x^2+6\\ c,=\left(2x-1\right)^2-2\left(2x-1\right)\left(2x+1\right)+\left(2x+1\right)^2\\ =\left(2x+1-2x+1\right)^2=4\)

Có thể giúp mình thực hiện cách chi tiết ko ạ ? Gv dạy mik ko hiểu mấy

\(a,=x^2-4-x^2-2x-1=-2x-5\\ b,=8x^3-1-8x^3-1=-2\\ 3,\\ a,\Rightarrow x^3+8-x^3+2x=15\\ \Rightarrow2x=7\Rightarrow x=\dfrac{7}{2}\\ b,\Rightarrow x^3-3x^2+3x-1-x^3+3x^2+4x=13\\ \Rightarrow7x=14\Rightarrow x=2\)

Bài 2:

a) \(=x^2-4-x^2-2x-1=-2x-5\)

b) \(=8x^3-1-8x^3-1=-2\)

Bài 3:

a) \(\Rightarrow x^3+8-x^3+2x=15\)

\(\Rightarrow2x=7\Rightarrow x=\dfrac{7}{2}\)

b) \(\Rightarrow x^3-3x^2+3x-1-x^3+3x^2+4x=13\)

\(\Rightarrow7x=14\Rightarrow x=2\)