cho tam giác ABC có góc B tù. Vẽ AH vuông góc BC, trên tia AH lấy điểm D sao cho H là trung điểm của AD.
a)C/m BA=BD
b)C/m CB là vphaan giác góc ACD
c)gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME=MA. C/m AC//BE
Cho tam giác ABC có ba góc nhọn (AB < AC) và M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh: Tam giác AMB = Tam giác DMC
b) Chứng minh: AB // CD
c) Vẽ AH vuông góc với BC (H thuộc BC). Trên tia đối của tia HA lấy điểm E sao cho HE = HA. Chứng minh: ME = MD.
d) Gọi K là trung điểm của ED. Chứng minh MK vuông góc với BC.

a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)
Bìa 1:
Cho tam giác nhọn ABC(AB < AC). Gọi M là trung điểm của BC. Trên tia đối của
tia MA lấy điểm D sao cho M là trung điểm của AD.
a) Chứng minh rằng: AMBA = AMCD.
b) Kẻ AH vuông góc với BC tại H và DK vuông góc với BC tại K. Chứng minh rằng: AH= DK.
c) Tia phân giác của ABC cắt AH và AM lần lượt tại I và E. Tia phân giác của BCD cắt KD và
MD lần lượt tại J và F. Chứng minh rằng: ABIA = ACJD.
d) Chứng minh rằng: I, M, J thẳng hàng.
Bài 4: (3,5 điểm)
Cho tam giác ABC có ba góc nhọn ( AB < AC), M là trung điểm của cạnh BC. Trên tia AM lấy điểm D sao cho M là trung điểm của AD.
a) Chứng minh: ∆AMB = ∆DMC
b) Chứng minh : AB//CD
c) Kẻ AH vuông góc với BC tại H trên tia AH lấy điểm K sao cho H là trung điểm của AK. Chứng minh MH là phân giác của góc AMK
a/ Xét △ABM và △DMC có:
AM=MD(gt)
MB=MC(gt)
^AMB=^CMD(đối đỉnh)
⇒ΔAMB=ΔDMC(cmt)(đpcm).
b/ Ta có: ΔAMB=ΔDMC(cmt)
⇒^MAB=^MDC⇒^MAB=^MDC[ hai góc ở vị trí so le trong]
Vậy: AB // CD (đpcm).
cho tam giác abc vuông tại a , biết ab = 6 cm , ac = 8 cm . gọi m là trung điểm của bc trên tia đối của tia ma lấy điểm d sao cho md = ma . vẽ AH vuông góc với BC tại H trên tia đối của tia HA lấy điểm E sao cho HE = HA. chứng minh CA vuông góc với CD
em tự vẽ hình nha
xét △AMB và △DMC có:
BM = MC
AM = MD
góc AMB = góc DMC ( đối đỉnh )
=> △AMB = △DMC
=> góc ABM = góc DCM và ở vị trí sole trong
=> AB // CD
ta có AB vuông góc với AC
=> CD vuông góc với AC ( đpcm )
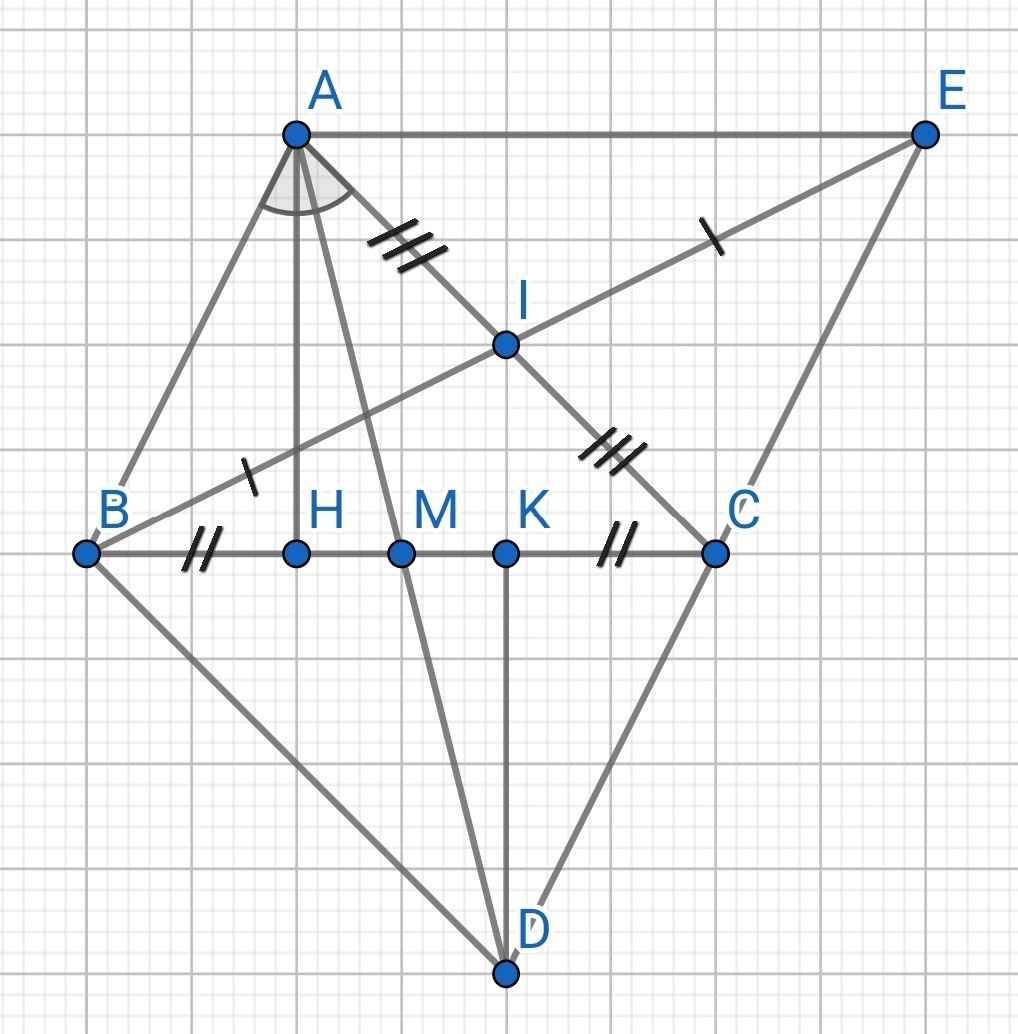
Cho tam giác ABC, vẽ điểm M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD.c)Kẻ AH vuông góc với BC, DK vuông góc BC (H,K thuộc BC). Chứng minh BK=CH d)Gọi I là trung điểm của AC, vẽ điểm E sao cho I là trung điểm của BE. Chứng minh C là trung điểm của DE
 c) Do M là trung điểm của BC (gt)
c) Do M là trung điểm của BC (gt)
⇒ BM = MC
Xét hai tam giác vuông: ∆AHM và ∆DKM có:
MA = MD (gt)
∠AMH = ∠DMK (đối đỉnh)
⇒ ∆AHM = ∆DKM (cạnh huyền - góc nhọn)
⇒ HM = KM (hai cạnh tương ứng)
Ta có:
BK = BM + KM
CH = CM + HM
Mà BM = CM (cmt)
KM = HM (cmt)
⇒ BK = CH
d) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
⇒ AB // DC và AB = DC
Tứ giác ABCE có:
I là trung điểm của AC (gt)
I là trung điểm của BE (gt)
⇒ ABCE là hình bình hành
⇒ AB // CE và AB = CE
Do AB // CE (cmt)
AB // DC (cmt)
⇒ C, D, E thẳng hàng (theo tiên đề Ơ-clít)
Ta có:
AB = CE (cmt)
AB = DC (cmt)
⇒ CD = CE
⇒ C là trung điểm của DE
Cho tam giác ABC đều. Lấy điểm E trên tia đối của tia CB sao cho C là trung điểm của đoạn thẳng BE
a. Chứng minh AB=AC=BC=CE
b. Chứng minh tam giác ABE là tam giác vuông
c. Vẽ AH vuông góc BC (H thuộc BC). Trên tia AH lấy điểm D sao cho H là trung điểm của AD. Chứng minh HB=HC
d. Chứng minh C là trọng tâm tam giác ADE
a: Vì ΔABC đều
nên AB=AC=BC
mà BC=CE
nên AB=AC=BC=CE
b: Xét ΔABE có
AC là đường trung tuyến
AC=BE/2
Do đó: ΔABE vuông tại A
c: Ta có; ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Cho tam giác ABC gọi M là trung điểm của cạnh BC trên tia đối của tia MA lấy điểm D sao cho MD = MA A CM AB=CD AC VUÔNG GÓC DC B CM MA=MB=MC C KẺ AH VUÔNG GÓC BC TẠI H CM AH<=BC/2
Cho tam giác ABC có 3 góc nhọn, đường cao AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD.
a) Chứng minh: tam giác AHB = tam giác DHB
b) Chứng minh rằng: BC là tia phân giác của góc ABD
c) Gọi M là trung điểm của Bc. Trên tia đối của tia MA lấy điểm F sao cho MF = MA. Từ F kẻ FN vuông góc với BC (N thuộc BC). Chứng minh: HD = NF
a) Xét \(\Delta\)AHB và \(\Delta\)DHB có:
^AHB = ^DHB ( 1v )
HA = HD ( giả thiết )
MH chung
=> \(\Delta\)AHB = \(\Delta\)DHB ( c.g.c)
b) Từ (a) => ^ABH = ^DHB => BH là phân giác ^ABD
Vì \(\Delta\)ABC nhọn => H nằm trong đoạn BC
=> BC là phân giác ^ABD
c) NF vuông BC
AH vuông BC
=> NF // AH
=> ^NFM = ^HAM ( So le trong )
Lại có: ^HMA = NMF ( đối đỉnh ) và MA = MF ( giả thiết )
=> \(\Delta\)NFM = \(\Delta\)HAM ( g.c.g)
=> NF = AH ( 2)
Từ ( a) => AH = HD ( 3)
Từ (2) ; (3) => NF = HD
Cho tam giác ABC. Gọi M là trung điểm của của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Kẻ đường cao AH. Trên tia AH lấy điểm E sao cho H là trung điểm AE.
a, CD//AB
b, CD=BE
c, CD vuông góc BD
d, ED//BC
a: Xét tứ giác ABDC có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AD
Do đó: ABDC là hình bình hành
Suy ra: CD//AB
b: Ta có: ABDC là hình bình hành
nên AB=CD(1)
Xét ΔBAE có
BH là đường cao ứng với cạnh AE
BH là đường trung tuyến ứng với cạnh AE
Do đó: ΔBAE cân tại B
Suy ra: AB=BE(2)
Từ (1) và (2) suy ra BE=CD
d: Xét ΔAED có
M là trung điểm của AD
H là trung điểm của AE
Do đó: MH là đường trung bình của ΔAED
Suy ra: MH//ED
hay ED//BC