Giải giúp em câu b ạ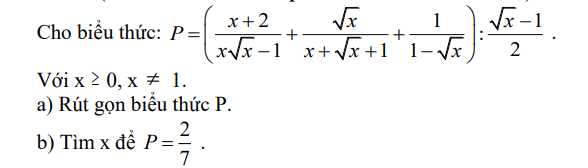

Những câu hỏi liên quan
Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.Lời giải câu a,b,c của em:
Đọc tiếp

Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.
Lời giải câu a,b,c của em:
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
Đúng 0
Bình luận (0)
Dạ giải giúp em với ạ mai em phải nộp rồi ạ
Nếu được thì giải hộ em câu b,c thôi cũng được ạ
a: góc OBA+góc OCA=90+90=180 độ
=>ABOC nội tiếp
b: góc OIE=góc OCE=90 độ
=>OICE là tứ giác nội tiếp
=>góc OEI=góc OCI
=>góc OEI=góc OCB
OBAC nội tiếp
=>góc OCB=góc OAB
=>góc OEI=góc OAB
=>góc OEI=góc OAI
=>OIAE nội tiếp
Đúng 0
Bình luận (0)
Giải giúp em câu bcdef với ạ riêng b,e,f giải đưa về cos giúp em
b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)
Đúng 1
Bình luận (0)
d.
\(\Leftrightarrow\dfrac{\sqrt{2}}{2}sinx-\dfrac{\sqrt{2}}{2}cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
giúp mình cái này với ạ!:< ở câu b ý ạ câu a em giải rồi ạ!
Giải giúp em câu b với, câu b thôi nha. Em cảm ơn nhiều ạ! 
Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)
Đúng 2
Bình luận (1)
Giải giúp em câu b ạ

Phương trình hoành độ giao điểm (d) và (P):
\(x^2=x-m+3\Leftrightarrow x^2-x+m-3=0\) (1)
\(\Delta=1-4\left(m-3\right)=13-4m\)
(d) cắt (P) tại 2 điểm pb khi \(13-4m>0\Rightarrow m< \dfrac{13}{4}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m-3\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}y_1=x_1^2\\y_2=x_2^2\end{matrix}\right.\)
\(\sqrt{y_1}+\sqrt{y_2}=1\Leftrightarrow\sqrt{x_1^2}+\sqrt{x_2^2}=1\)
\(\Leftrightarrow\left|x_1\right|+\left|x_2\right|=1\)
\(\Leftrightarrow x_1^2+x_2^2-2\left|x_1x_2\right|=1\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left|x_1x_2\right|=1\)
\(\Leftrightarrow1-2\left(m-3\right)+2\left|m-3\right|=1\)
\(\Leftrightarrow m-3=\left|m-3\right|\)
\(\Rightarrow m\ge3\)
Kết hợp điều kiện ban đầu ta được: \(3\le m< \dfrac{13}{4}\)
Đúng 2
Bình luận (0)
Giải giúp em câu b với ạ

a: \(\Leftrightarrow\left\{{}\begin{matrix}2x+y=1\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+2y=2\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=1-2x=1-\dfrac{2}{3}=\dfrac{1}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)

giải giúp em câu b, với ạ
Giải giúp em câu a,b,c với ạ !
c: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AB^2=64-32=32\)
hay \(AB=4\sqrt{2}\left(cm\right)\)
Xét ΔABC vuông tại A có AB=AC
nên ΔBAC vuông cân tại A
Suy ra: \(\widehat{B}=\widehat{C}=45^0\)
Đúng 0
Bình luận (0)
Giải giúp em câu b bài 2 với ạ

















