Xác định tâm và bán kính đường tròn ngoại tiếp hình chữ nhật ABCD trong mỗi trường hợp sau:
a) AB = 6 cm, BC = 8 cm; b) AC = 9cm.
Cho tam giác ABC có đường cao AH = 4 cm Độ dài các hình chiếu vuông góc của AB và AC lên BC lần lượt là 2cm và 8cm. Xác định tâm và bán kính các đường tròn ngoại tiếp tam giác ABC. Giúp mình với🙏🙏
Cho hình chữ nhật ABCD có chiều dài AB=2a,chiều rộng BC=a.Kẻ tia phân giác của góc ACD,từ A hạ AH vuông góc với đường phân giác nói trên
a,Chứng minh:AHCD nội tiếp trong đường tròn tâm O mà ta phải xác định rõ tâm và bán kính theo a
b,HB cắt AD tại I và cắt AC tại M;HC cắt DB tại N.Chứng tỏ HB=HC và AB.AC=BH.BI
c,Chứng tỏ MN song song với tiếp tuyến tại H của (O)
d,Từ D kẻ đường thẳng song song với BH;đường này cắt HC ở K và cắt (O) ở J.Chứng minh HOKD nội tiếp
Cho đường tròn tâm O, bán kính R = 6cm ngoại tiếp tam giác ABC vuông tại A có AB = 6cm, AC = 8 cm. Trong các dây AB, BC và AC thì dây nào gần tâm hơn?
A. AB
B. BC
C. AC
D. chưa kết luận được.
Đáp án B
Áp dụng định lí Pytago vào tam giác ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100 nên BC =10 cm
Ta có: AB < AC < BC ( 6 cm < 8 cm < 10 cm )
Do đó, dây BC gần tâm nhất, dây AB xa tâm nhất
Cho hình chữ Nhật ABCD, ab=12cm, bc=9cm chứng minh rằng các điểm A,b, C , D cùng thuộc một đường tròn. Xác định tâm và bán kính đường tròn đó
Cho hình chữ nhật ABCD có AB=12 cm, BC=5 cm. Tìm tâm và bán kính của đường trong đi qua 4 điểm A,B,C,D
Gọi O là giao của AC và BD
ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
ABCD là hình chữ nhật
=>góc ABC=góc BCD=góc CDA=góc BAD=90 độ
góc B+góc D=180 độ
=>ABCD là tứ giác nội tiếp đường tròn đường kính AC
=>O là tâm của đường tròn ngoại tiếp tứ giác ABCD
ABCD là hình chữ nhật
=>góc BAD=90 độ
=>BD^2=AB^2+AD^2
=>\(BD=\sqrt{12^2+5^2}=13\left(cm\right)\)
=>R=BD/2=6,5(cm)
Cho hình chữ Nhật ABCD, ABCD=12cm, BC=9cm. Chứng minh rằng các điểm A, B, C, D cùng thuộc một đường tròn. Xác định tâm và bán kính đường tròn đó
Tứ giác abcd nội tiếp đường tròn đường kính AB, có AB=BC=4 căn 3 cm, CD=4cm. Bán kính đường tròn ngoại tiếp tứ giác ABCD là?
Vẽ hình bình hành
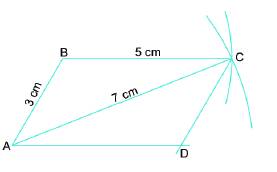
Vẽ hình bình hành ABCD khi biết AB = 3cm, BC = 5 cm và đường chéo AC = 7 cm theo hướng dẫn sau:
- Vẽ đoạn thẳng AB= 3 cm.
- Vẽ đường tròn tâm A bán kính 7 cm; vẽ đường tròn tâm B bán kính 5 cm; hai đường tròn cắt nhau tại C. nối B với C.
- Từ A kẻ đường thẳng song song với BC; từ C kẻ đường thẳng song song với AB; hai đường thẳng này cắt nhau tại D.
ABCD là hình bình hành cần vẽ.
- Dùng compa để kiểm tra xem các cạnh đối diện có bằng nhau hay không?
- Đặt một đầu compa tại điểm B đầu còn lại tại điểm C. Giữ nguyên compa và đặt một đầu tại điểm A, nếu đầu còn lại trùng với điểm D thì BC = AD.
- Đặt một đầu compa tại điểm B đầu còn lại tại điểm A. Giữ nguyên compa và đặt một đầu tại điểm C, nếu đầu còn lại trùng với điểm D thì AB = CD.
- Qua kiểm tra ta thấy BC = AD và AB = CD.
Cho ∆ABC vuông tại A, đường cao AH= 2R. Gọi D,E lần lượt là hình chiếu của H trên AB,AC. Gọi M,N lần lượt là trung điểm của BH,CH. a) CM: Tứ giác ADHE nội tiếp; xác định tâm O và bán kính đường tròn ngoại tiếp tứ giác ADHE. b) CM: ∆ BHO ~ ∆ AHN.
a: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
Tâm O là trung điểm của AH
bán kính là AH/2=R
b:
ΔABC vuông tại A có AH là đường cao
nên HA^2=HB*HC
=>HA/HC=HB/HA
HO/HN=HA/HC=HB/HA
Xét ΔBHO vuông tại H và ΔAHN vuông tại H có
HB/HA=HO/HN
=>ΔBHO đồng dạng với ΔAHN
Tứ giác ABCD nội tiếp đường tròn đường kính AD, có AB = BC = 4√3cm; CD = 4cm. Bán kính đường tròn ngoại tiếp tứ giác ABCD là ............ cm.
Lời giải:
Gọi giao của $BO$ và $AC$ là $H$
Vì $BA=BC; OA=OC$ nên $BO$ là trung trực của $AC$
$\Rightarrow BO$ vuông góc với $AC$ tại trung điểm $H$ của $AC$.
Do đó $HO$ là đường trung bình ứng với cạnh $CD$ của tam giác $ACD$
$\Rightarrow HO=2$
$BH=BO-HO=R-2$
Theo định lý Pitago:
$BC^2-BH^2=CH^2=CO^2-HO^2$
$\Leftrightarrow (4\sqrt{3})^2-(R-2)^2=R^2-2^2$
$\Leftrightarrow 48-(R-2)^2=R^2-4$
$\Rightarrow R=6$ (cm)