Cho tam giác nhọn ABC. Gọi A’, B’, C’ lần lượt là chân đường cao kẻ từ A, B, C và H là trực tâm của tam giác đó. Hãy chỉ ra các tứ giác nội tiếp trong hình.

Những câu hỏi liên quan
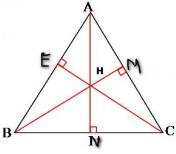
CHO tam giác ABC có 3 góc nhọn (AB<AC) NỘI TIẾP tam giác đường tròn (o) gọi H là trực tâm và M, N, P lần lượt là chân đường cao kẻ từ các đỉnh A, B, C của tam giác ABC.
a) CM:các tứ giác APHN và BPNC nội tiếp
b) CM; H LÀ tâm đường tròn nội tiếp tam giác MNP
VẼ hình hộ mk vs ạ![]()
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Gọi D,E,K lần lượt là chân đường cao kẻ từ A,B,C của tam giác ABC . H là trực tâm của tam giác ABC
a,CM: tứ giác HDCE nội tiếp
b, Gọi M là giao điểm của AH và (O). Chứng minh D là trung điểm của HM
c,Chứng minh: OA vuông góc với EK
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC
Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E

a) ∆HBC có:
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Vậy A là trực tâm của ∆HBC
b) Tương tự trực tâm của ∆AHB là C, ∆AHC là B
Đúng 0
Bình luận (0)
Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, Ac, AB tại N, M, E.
a) ΔHBC có :
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Vậy A là trực tâm của ΔHBC.
b) Tương tự, trực tâm của ΔAHB là C; ΔAHC là B.
Đúng 0
Bình luận (0)
cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O và có H là trực tâm.Gọi E,F lần lượt là các chân đường cao kẻ từ các đỉnh B và C của tam giacABC; M là trung điểm cạnh BC. chứng minh ;
a) các tứ giác AEHFva BCEF nội tiếp
b) AH=2OM và OA vuông góc với EF
cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Gọi A', B', C' là chân các đường vuông góc kẻ từ A,B,C trên các cạnh BC, AC, AB. H là trực tâm của tam giác ABC. a,Cmr AA' là đường phân giác trong của góc B'A'C'.b, Cho góc BAC = 60 độ . Chứng tỏ tam giác AOH cân
Xem chi tiết
cho tam giác ABC có ba góc nhọn đường cao BE . gọi H và K lần lượt là chân các đường vuông góc kẻ từ E đến AB , AC
a, CMR tứ giác BHEK nội tiếp
b, CMR : BH. BA = BK . BC
c, gọi F là chân các đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm của đoạn thẳng EF . CMR H ,I , K thẳng hàng
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ta trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB, HAC
Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E
a) ∆HBC có:
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Vậy A là trực tâm của ∆HBC
b) Tương tự trực tâm của ∆AHB là C, ∆AHC là B
Đúng 0
Bình luận (0)
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ta trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB, HAC
Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E
a) ∆HBC có:
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Vậy A là trực tâm của ∆HBC
b) Tương tự trực tâm của ∆AHB là C, ∆AHC là B
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn không cân, nội tiếp đường tròn O. Gọi H là trực tâm và I, K lần lượt là chân đường cao kẻ từ đỉnh A, B của tam giác ABC. ( I thuộc BC, K thuộc AC). Gọi M là trung điểm của BC. Kẻ HJ vuông góc với AM ( J thuộc AM) a, CM : A,H,J,K cùng thuộc 1 đường tròn và góc IHK = góc MJK b, CM : tam giác AJK đồng dạng với tam giác ACM c, CM : MJ.MA < R2
Cho tam giác ABC nhọn có trực tâm H. Gọi M,N lần lượt là chân đường cao hạ từ B,C của tam giác ABC. Lấy D thuộc BC( D khác B,C), E là giao điểm của đường tròn ngoại tiếp tam giác CDM và đường tròn ngoại tiếp tam giác BDN(E khác B). CMR: A,E,D thẳng hàng
Ta có ^MEN = ^NBD + ^MCD = 1800 - ^MAN. Suy ra tứ giác AMEN nội tiếp
Cũng dễ có tứ giác BCMN nội tiếp đường tròn (BC)
Từ đó ^AEM = ^ANM = ^MCB = ^MCD = 1800 - ^MED. Hay ^AEM + ^MED = 1800
Vậy thì A,E,D thẳng hàng (đpcm).
Đúng 0
Bình luận (0)

Ta có ^BCN = ^BMN ( do tứ giác BNMC nội tiếp )
=> ^NBC = ^AMN ( cùng phụ với hai góc bằng nhau ) (1)
Mặt khác do BDEN và CDEM là các tứ giác nội tiếp chung cạnh DE
Nên ^NBD + ^MCD = ^NEM ( tính chất góc ngoài tứ giác nội tiếp )
Mà ^NBD + ^MCD + ^NAM = 1800
Suy ra ^NEM + ^NAM = 1800 . Vây AMEN nội tiếp
Do đó: ^AMN = ^AEN (2)
Từ (1) và (2) suy ra ^NBD = ^AEN
Mà ^NBD + ^DEN = 1800 (do BDEN nội tiếp)
Nên ^DEN + ^AEN = 1800 => ^AED=1800 .
Vậy ba điểm A, E, D thẳng hàng (đpcm)