Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông và hình chữ nhật trong Hình 11.
Những câu hỏi liên quan
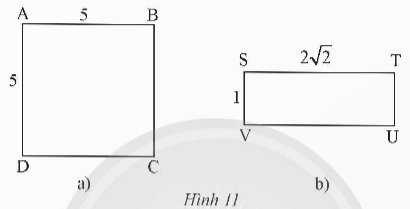
Hãy xác định tâm và bán kính đường tròn ngoại tiếp của các hình sau:
1, Hình vuông 3, hình thang cân
2, HCN. 4, hình bình hành
1) tâm : giao điểm của 2 đường chéo bán kính \(\frac{r}{\sqrt{2}}\)( với r là cạnh hình vuông )
2) tâm : giao điểm của 2 đường chéo bán kính \(\frac{1}{2}\sqrt{a^2+b^2}\)( với a,b là các cạnh của hình vuông)
3) tâm : giao điểm của 2 đường chéo
4) không có tâm
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có chiều dài AB2a,chiều rộng BCa.Kẻ tia phân giác của góc ACD,từ A hạ AH vuông góc với đường phân giác nói trêna,Chứng minh:AHCD nội tiếp trong đường tròn tâm O mà ta phải xác định rõ tâm và bán kính theo ab,HB cắt AD tại I và cắt AC tại M;HC cắt DB tại N.Chứng tỏ HBHC và AB.ACBH.BIc,Chứng tỏ MN song song với tiếp tuyến tại H của (O)d,Từ D kẻ đường thẳng song song với BH;đường này cắt HC ở K và cắt (O) ở J.Chứng minh HOKD nội tiếp
Đọc tiếp
Cho hình chữ nhật ABCD có chiều dài AB=2a,chiều rộng BC=a.Kẻ tia phân giác của góc ACD,từ A hạ AH vuông góc với đường phân giác nói trên
a,Chứng minh:AHCD nội tiếp trong đường tròn tâm O mà ta phải xác định rõ tâm và bán kính theo a
b,HB cắt AD tại I và cắt AC tại M;HC cắt DB tại N.Chứng tỏ HB=HC và AB.AC=BH.BI
c,Chứng tỏ MN song song với tiếp tuyến tại H của (O)
d,Từ D kẻ đường thẳng song song với BH;đường này cắt HC ở K và cắt (O) ở J.Chứng minh HOKD nội tiếp
Cho tam giác ABC vuông tại A, ∠ABC = 60◦
, AB = a.
a) Xác định tâm O và tính bán kính đường tròn ngoại tiếp tam giác ABC.
b) Vẽ đường cao AH. Đường tròn đường kính BH cắt AB tại D và đường tròn đường
kính CH cắt AC tại E. Tứ giác ADHE là hình gì? Tính DE.
c) Chứng minh rằng AO⊥DE.
a: O là trung điểm của BC
b: Xét \(\left(\dfrac{BH}{2}\right)\) có
ΔBDH là tam giác nội tiếp
BH là đường kính
Do đó: ΔBDH vuông tại D
Xét \(\left(\dfrac{CH}{2}\right)\)có
ΔCHE nội tiếp đường tròn
CH là đường kính
Do đó: ΔCHE vuông tại E
Xét tứ giác ADHE có
\(\widehat{AEH}=\widehat{ADH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
Đúng 0
Bình luận (1)
Cho đường tròn tâm O đường kính BC, A là một điểm thuộc đường tròn. H là hình chiếu của A trên BC. Vẽ đường tròn (I) có đường kính AH, cắt AB và AC theo thứ tự ở M và N.a) Chứng minh rằng OA vuông góc với MN.b) Vẽ đường kính AOK của đường tròn (O). Gọi E là trung điểm của HK. Chứng minh rằng E là tâm của đường tròn ngoại tiếp tứ giác BMNC.c) Cho BC cố định. Xác định vị trí của điểm A để bán kính của đường tròn ngoại tiếp tứ giác BMNC lớn nhất.
Đọc tiếp
Cho đường tròn tâm O đường kính BC, A là một điểm thuộc đường tròn. H là hình chiếu của A trên BC. Vẽ đường tròn (I) có đường kính AH, cắt AB và AC theo thứ tự ở M và N.
a) Chứng minh rằng OA vuông góc với MN.
b) Vẽ đường kính AOK của đường tròn (O). Gọi E là trung điểm của HK. Chứng minh rằng E là tâm của đường tròn ngoại tiếp tứ giác BMNC.
c) Cho BC cố định. Xác định vị trí của điểm A để bán kính của đường tròn ngoại tiếp tứ giác BMNC lớn nhất.
Cho tam giác ABC có đường cao AH = 4 cm Độ dài các hình chiếu vuông góc của AB và AC lên BC lần lượt là 2cm và 8cm. Xác định tâm và bán kính các đường tròn ngoại tiếp tam giác ABC. Giúp mình với🙏🙏
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD),
a
3
. Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng
a
3
3
, góc
A
C
B
^
30
∘
. Tính theo a thể tích khối chóp S.ABCD A.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD), a 3 . Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng a 3 3 , góc A C B ^ = 30 ∘ . Tính theo a thể tích khối chóp S.ABCD
A. 2 a 3 3
B. a 3 3
C. a 3 6
D. 4 a 3 3
Cho hình vuông ABCD có tâm O. Gọi R,r là bán kính đường tròn ngoại tiếp và nội tiếp hình vuông ABCD.Kẻ OH⊥CD,chứng minh OH=HD
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD),
S
A
a
3
. Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng
a
3
3
, góc
∠
A
C
B
30
°
. Tính theo a thể tích khối chóp S.ABCD A. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD), S A = a 3 . Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng a 3 3 , góc ∠ A C B = 30 ° . Tính theo a thể tích khối chóp S.ABCD
A. 2 a 3 3
B. a 3 3
C. 2 a 3 6
D. 4 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD),
S
A
a
3
. Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng
a
3
3
, góc
∠
A
C
B
30
°
. Tính theo a thể tích khối chóp S.ABCD A. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD), S A = a 3 . Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng a 3 3 , góc ∠ A C B = 30 ° . Tính theo a thể tích khối chóp S.ABCD
A. 2 a 3 3
B. a 3 3
C. 2 a 3 6
D. 4 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD),
S
A
a
3
. Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng
a
3
3
, góc
∠
A
C
B
30
°
. Tính theo a thể tích khối chóp S.ABCD A.
2
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng (ABCD), S A = a 3 . Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng a 3 3 , góc ∠ A C B = 30 ° . Tính theo a thể tích khối chóp S.ABCD
A. 2 a 3 3
B. a 3 3
C. 2 a 3 6
D. 4 a 3 3
