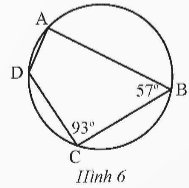
Tìm số đo các góc chưa biết của tứ giác ABCD trong Hình 6.
Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.

a) Trong tứ giác \(ABCD\) có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \\110^\circ + \widehat B + 75^\circ + 75^\circ = 360^\circ \\\widehat B = 360^\circ - \left( {110^\circ + 75^\circ + 75^\circ } \right)\\\widehat B = 100^\circ \end{array}\)
b) Trong tứ giác \(MNPQ\) ta có:
\(\begin{array}{l}\widehat P + \widehat Q + \widehat M + \widehat N = 360^\circ \\90^\circ + 70^\circ + \widehat M + 90^\circ = 360^\circ \\\widehat M = 360^\circ - \left( {90^\circ + 70^\circ + 90^\circ } \right)\\\widehat M = 110^\circ \end{array}\)
c) Ta có: \(\widehat {TSV} = 180^\circ - 60^\circ = 120^\circ \)
Xét tứ giác \(UTSV\) ta có:
\(\begin{array}{l}\widehat U + \widehat T + \widehat S + \widehat V = 360^\circ \\115^\circ + 65^\circ + 120^\circ + \widehat V = 360^\circ \\\widehat V = 360^\circ - \left( {115^\circ + 65^\circ + 120^\circ } \right)\\\widehat V = 60^\circ \end{array}\)
d) Trong tứ giác \(EFGH\) có:
\(\begin{array}{l}\widehat F + \widehat E + \widehat G + \widehat H = 360^\circ \\\widehat F + 80^\circ + 100^\circ + 70^\circ = 360^\circ \\\widehat F = 360^\circ - \left( {80^\circ + 100^\circ + 70^\circ } \right)\\\widehat F = 110^\circ \end{array}\)
Cho tứ giác ABCD biết số đo của các góc A, B, C, D tỉ lệ thuận với 1,2,3,4.
Tính số đo của các góc trong tứ giác ABCD.
cho tứ giác abcd có b=80 độ c= 100 độ
a cmr tứ giác abcd là hình thang
b tính số đo các góc a và d biết a:d = 6:4
\(a,=>\angle\left(B\right)+\angle\left(C\right)=100+80=180^o\)
mà 2 góc ở vị trí trong cùng phía \(=>AB//CD\)
=>ABCD là hình thang
b,\(\dfrac{\angle\left(A\right)}{\angle\left(D\right)}=\dfrac{6}{4}=>\angle\left(A\right)=\dfrac{6\angle\left(D\right)}{4}\)
\(=>\angle\left(A\right)+\angle\left(D\right)=180^o\)(góc trong cùng phía)
\(=>\dfrac{6\angle\left(D\right)}{4}+\angle\left(D\right)=180^o=>\angle\left(D\right)=72^o=>\angle\left(A\right)=\dfrac{6.72^0}{4}=108^o\)
a: Xét tứ giác ABCD có
\(\widehat{B}+\widehat{C}=180^0\)
nên ABCD là hình thang
Tìm số đo các góc chưa biết của các tam giác trong Hình 5.

a) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat B = {180^o} - \widehat A - \widehat C = {180^o} - {72^o} - {44^o} = {64^o}\end{array}\)
b) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow \widehat D = {180^o} - \widehat E - \widehat F = {180^o} - {59^o} - {31^o} = {90^o}\end{array}\)
c) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {120^o} - {33^o} = {27^o}\end{array}\)
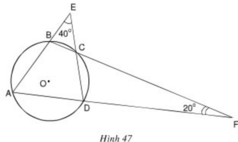
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.
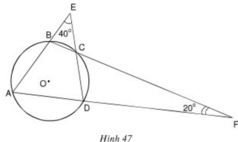
Ta có: B C E ^ = D C F ^ (hai góc đối đỉnh)
Đặt x = B C E ^ = D C F ^ . Theotinhs chất góc ngoài tam giác, ta có:
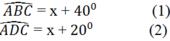
Lại có: ![]()
(Hai hóc đối điện tứ giác nội tiếp).
Từ (1),(2),(3) suy ra:
![]()
Từ (1), ta có: A B C ^ = 60 o + 40 o = 100 o
Từ (2), ta có: A D C ^ = 60 o + 20 o = 80 o
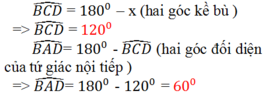
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.
Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.
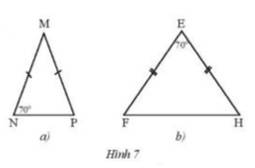
a) Vì \(\Delta MNP\) cân tại M ( theo giả thiết )
\( \Rightarrow \widehat N = \widehat P = {70^o}\) ( 2 góc đáy của tam giác cân )
\( \Rightarrow \widehat M = {180^o} - {2.70^o} = {40^o}\)
b) Xét \(\Delta EFH\) cân tại E
Theo định lí về tổng 3 góc trong tam giác ta có
\( \Rightarrow \widehat E + \widehat F + \widehat H = {180^o}\)
Mà \(\widehat F = \widehat H\)( tính chất tam giác cân )
\( \Rightarrow \widehat F = \widehat H = {180^o} - \widehat E = ({180^o} - {70^o}):2 = {55^o}\)
Tính các góc của tứ giác ABCD biết số đo của các góc tỉ lệ với các số
3: 6 : 4: 5
Áp dụng tc dtsbn:
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{6}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{D}}{5}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{3+6+4+5}=\dfrac{360^0}{18}=20^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=60^0\\\widehat{B}=120^0\\\widehat{C}=80^0\\\widehat{D}=100^0\end{matrix}\right.\)
Cho tứ giác ABCD có B=C=90°
tứ giác ABCD hình gì
Tính số đo các góc A và D biết A= 8x+6°, D =3x+9°
Tứ giác ABCD là hình thang vuông
Ta có B = C = 90*
=> B + C = 180*
=> A + D = 180* ( Vì tứ giác có 360 độ )
=> 8x + 6 + 3x + 9 = 180
<=> 11x + 15 =180
<=> 11x = 180 - 15 = 165*
x = 165 : 11 =15
=> A = 8 x 15 + 6 = 126*
D = 3 X 15 + 9 = 54
Vậy ....
Tứ giác \(EFGH\) có các góc cho như trong Hình 5.
a) Chứng minh rằng \(EFGH\) là hình thang
b) Tìm góc chưa biết của tứ giác
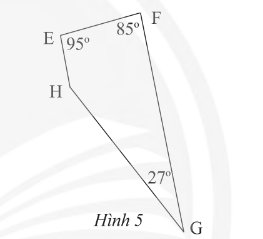
a) Ta có:
\(\widehat {\rm{E}} + \widehat {\rm{F}} = 95^\circ + 85^\circ = 180^\circ \)
Mà hai góc ở vị trí Trong cùng phía
Suy ra \(EH\;{\rm{//}}\;FG\)
Suy ra: \(EFGH\) là hình thang
b) Xét hình thang \(EFGH\) ta có: \(\widehat E + \widehat F + \widehat G + \widehat H = 360^\circ \)
\(\begin{array}{l}95^\circ + 85^\circ + 27^\circ + \widehat H = 360^\circ \\\widehat H = 153^\circ \end{array}\)