a) Xác suất thực nghiệm của biến cố “Lấy được bóng xanh” sau 200 lần thử là \(\frac{{62}}{{200}} = \frac{{31}}{{100}}\).

b) Gọi \(N\) là tổng số quả bóng đỏ trong hộp.

Tổng số quả bóng trong hộp là \(N + 20\).

Xác suất thực nghiệm của biến cố “Lấy được bóng đỏ” sau 200 lần thử là \(\frac{{138}}{{200}} = \frac{{69}}{{100}}\).

Xác suất lí thuyết để “Lấy được bóng đỏ” là \(\frac{N}{{N + 20}}\).

Do số lần lấy bóng là 200 lần đủ lớn nên

\(\frac{N}{{N + 20}} \approx \frac{{69}}{{100}} \Leftrightarrow 100N \approx 69N + 1380 \Leftrightarrow 31N \approx 1380 \Leftrightarrow N \approx 45\)

Vậy có khoảng 45 quả bóng đỏ trong hộp.

Do lần đầu tiên lấy bóng sau đó trả lại hộp nên lần hai có thể lấy 1 trong 4 quả bóng và hai lần lấy lần lượt nên ta cần phải tính đến thứ tự lấy bóng. Nếu lần đầu lấy được bóng 1 và lần hai lấy được bóng 3 thì ta sẽ kí hiệu kết quả của phép thử là cặp (1; 3). Khi đó không gian mẫu của phép thử là:

\(\Omega  = \left\{ \begin{array}{l}(1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(2;4);\\(3;1);(3;2);(3;3);(3;4);(4;1);(4;2);(4;3);(4;4)\end{array} \right\}\)

Chọn đáp án C

Các trường hợp thuận lợi cho biến cố là

§ (Giải thích: Khi bốc mình sẽ bốc bi ít hơn trước tiên. Bốc 2 viên bi xanh từ 4 viên bi xanh nên có  cách, tiếp theo bốc 1 viên bi vàng từ 3 viên bi vàng (do loại 2 viên cùng số với bi xanh đã bốc) nên có C 3 1  cách, cuối cùng bốc 1 viên bi đỏ từ 3 viên bi đỏ (do loại 2 viên cùng số với bi xanh và 1 viên cùng số với bi vàng) nên có  C 3 1  cách).

Số phần tử của không gian mẫu là 

Các trường hợp thuận lợi cho biến cố là

• 2 xanh,  1 vàng, 1  đỏ (Giải thích: Khi bốc mình sẽ bốc bi ít hơn trước tiên. Bốc 2 viên bi xanh từ 4 viên bi xanh nên có 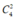 cách, tiếp theo bốc 1 viên bi vàng từ 3 viên bi vàng (do loại 2 viên cùng số với bi xanh đã bốc) nên có  cách, cuối cùng bốc 1 viên bi đỏ từ 3 viên bi đỏ (do loại 2 viên cùng số với bi xanh và 1 viên cùng số với bi vàng) nên có  cách)

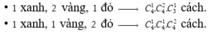
Suy ra số phần tử của biến cố là 

Vậy xác suất cần tính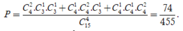 

Chọn C.

a) Xác suất lí thuyết của biến cố “An lấy được bóng xanh” là

\({P_1} = \frac{3}{5}\).

b) Xác suất An lấy được bóng xanh sau 20 lần là:

\({P_2} = \frac{9}{{20}}\)

Xác suất An lấy được bóng xanh sau 40 lần là:

\({P_3} = \frac{{20}}{{40}} = \frac{1}{2}\)

Xác suất An lấy được bóng xanh sau 60 lần là:

\({P_4} = \frac{{32}}{{60}} = \frac{8}{{15}}\)

Xác suất An lấy được bóng xanh sau 80 lần là:

\({P_5} = \frac{{46}}{{80}} = \frac{{23}}{{40}}\)

Xác suất An lấy được bóng xanh sau 100 lần là:

\({P_6} = \frac{{59}}{{100}}\)

-Ta cần phải lấy bóng ở trong hộp ghi Trắng-Đen, bởi vì họ dán nhãn sai nên trong đó có 2 quả bóng cùng màu trắng hoặc đen.

-Khi ta lấy được quả bóng có 1 màu nào đó thì ta sẽ biết được hộp Trắng-Đen chứa 2 quả bóng cùng màu ấy. Gọi màu đó là màu a và màu còn lại là màu b thì:

-Khi xác định màu bóng trong  hộp dán nhãn a-a thì chắc chắn trong đó sẽ không có 2 màu bóng a-b được bởi nếu vậy thì màu hộp a-b đã chứa bóng màu a-a hộp a-a sẽ chứa bóng màu a-b => hộp b-b sẽ chứa bóng màu b-b, lại trái đề bài là họ đều dán nhãn sai. Vậy trong hộp a-a sẽ có màu bóng là b-b và hộp b-b sẽ chứa bóng màu a-b.

Ta đã xác định được màu bóng trong 3 hộp!

bạn Ngô Văn Phương trả lời rối quá

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega  \right) = C_{13}^2.13\)

a) Biến cố “Ba quả bóng lấy ra cùng màu” xảy ra khi hai lần đều lấy ra bóng có cùng màu xanh, đỏ hoặc vàng. Số kết quả thuận lợi cho biến cố là \(C_5^2.5 + C_6^2.6 + C_2^2.2 = 142\)

Vậy xác suất của biến cố “Ba quả bóng lấy ra cùng màu” là \(P = \frac{{142}}{{13C_{13}^2}} = \frac{{71}}{{507}}\)

b) Số kết quả thuận lợi cho biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(C_{13}^2.5\)

Vậy xác suất của biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(P = \frac{{5C_{13}^2}}{{13C_{13}^2}} = \frac{5}{{13}}\)

c) Biến cố “Ba bóng lấy ra có ba màu khác nhau” xảy ra khi hai quả bóng lấy ra lần đầu là 2 màu khác nhau và quả bóng lấy lần 2 có màu còn lại. Số kết quả thuận lợi cho biến cố này là \(5.6.2.3 = 180\)

Vậy xác suất của biến cố “Ba bóng lấy ra có ba màu khác nhau” là \(P = \frac{{180}}{{13C_{13}^2}} = \frac{{30}}{{169}}\)

+) Số trung bình: \(\overline x  = \frac{{0.10 + 1.30 + 2.40 + 3.20}}{{100}} = 1,7\)

+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)

Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm, \(\underbrace {0,...,0}_{10},\underbrace {1,...,1}_{30},\underbrace {2,...,2}_{40},\underbrace {3,...,3}_{20}.\)

Bước 2: Vì \(n = 100\), là số chẵn nên \({Q_2} = \frac{1}{2}(2 + 2) = 2\)

\({Q_1}\) là trung vị của nửa số liệu:  \(\underbrace {0,...,0}_{10},\underbrace {1,...,1}_{30},\underbrace {2,...,2}_{10}.\) Do đó \({Q_1} = \frac{1}{2}(1 + 1) = 1\)

\({Q_3}\) là trung vị của nửa số liệu \(\underbrace {2,...,2}_{30},\underbrace {3,...,3}_{20}.\) Do đó \({Q_3} = \frac{1}{2}(2 + 2) = 2\)

+) Mốt \({M_o} = 2\)