Bác An thống kê lại số cuộc gọi điện thoại mà mình thực hiện mỗi ngày trong tháng 7 ở bảng tần số như sau:

Hãy vẽ biểu đồ cột và biểu đồ đoạn thẳng biểu diễn mẫu số liệu trên.
Cho bảng thống kê số tiết học các nội dung trong môn Toán của hai khối lớp 6 và lớp 8 như sau:
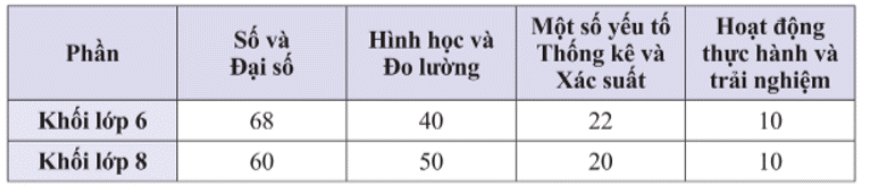
Hãy biểu diễn tập dữ liệu trên dưới dạng:
a) Hai biểu đồ cột.
b) Một biểu đồ cột kép.
Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong 2 một tuần ở bảng sau:

Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.
Số cuộc gọi của người đó trong một tuần là \(n = 8 + 10 + 7 + 5 + 2 + 1 = 33\).
Gọi \({x_1};{x_2};...;{x_{33}}\) là thời gian thực hiện cuộc gọi của người đó trong một tuần được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_8} \in \left[ {0;60} \right);{x_9},...,{x_{18}} \in \left[ {60;120} \right);{x_{19}},...,{x_{25}} \in \left[ {120;180} \right);{x_{26}},...,{x_{30}} \in \left[ {180;240} \right);\) \({x_{31}},{x_{32}} \in \left[ {240;300} \right);{x_{33}} \in \left[ {300;360} \right)\).
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{17}}\) thuộc nhóm \(\begin{array}{*{20}{l}}{\left[ {60;120} \right)}\end{array}\)
Ta có: \(n = 33;{n_m} = 10;C = 8;{u_m} = 60;{u_{m + 1}} = 120\)
Tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 60 + \frac{{\frac{{33}}{2} - 8}}{{10}}.\left( {120 - 60} \right) = 111\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_8} + {x_9}} \right)\).
Do \({x_8} \in \left[ {0;60} \right),{x_9} \in \left[ {60;120} \right)\) nên tứ phân vị thứ nhất của dãy số liệu là: \({Q_1} = 60\).
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{25}} + {x_{26}}} \right)\).
Do \({x_{25}} \in \left[ {120;180} \right),{x_{26}} \in \left[ {180;240} \right)\) nên tứ phân vị thứ ba của dãy số liệu là: \({Q_3} = 180\).
Cho bảng thống kê sau:
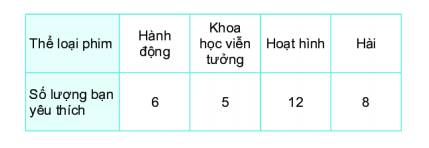
Hãy vẽ biểu đồ cột biểu diễn bảng thống kê trên.
Thống kê số huy chương bốn quốc gia dẫn đầu SEA Games 31 được cho trong bảng số liệu sau:
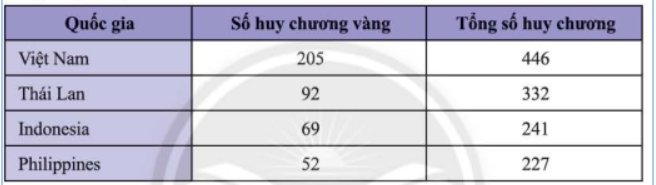
Hãy chuyển dữ liệu đã cho vào bảng thống kê theo mẫu dưới đây và vào biểu đồ cột kép tương ứng.

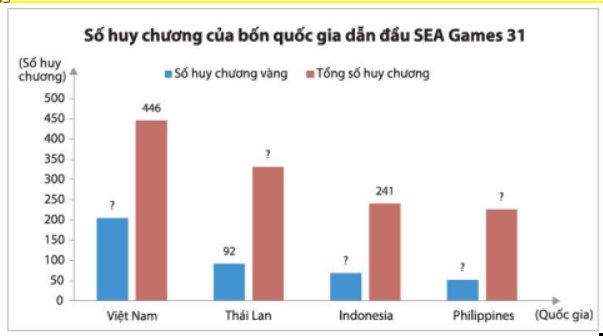
Điền số vào bảng: 446 92 69 227
Biểu đồ; 205 322 69 52 227
Xét bảng 2 (được lập ở bài tập mẫu của bài 1)
Để mô tả bảng 2 và trình bày các số liệu thống kê, người ta vẽ biểu đồ tần số hình cột dưới đây (h.55)
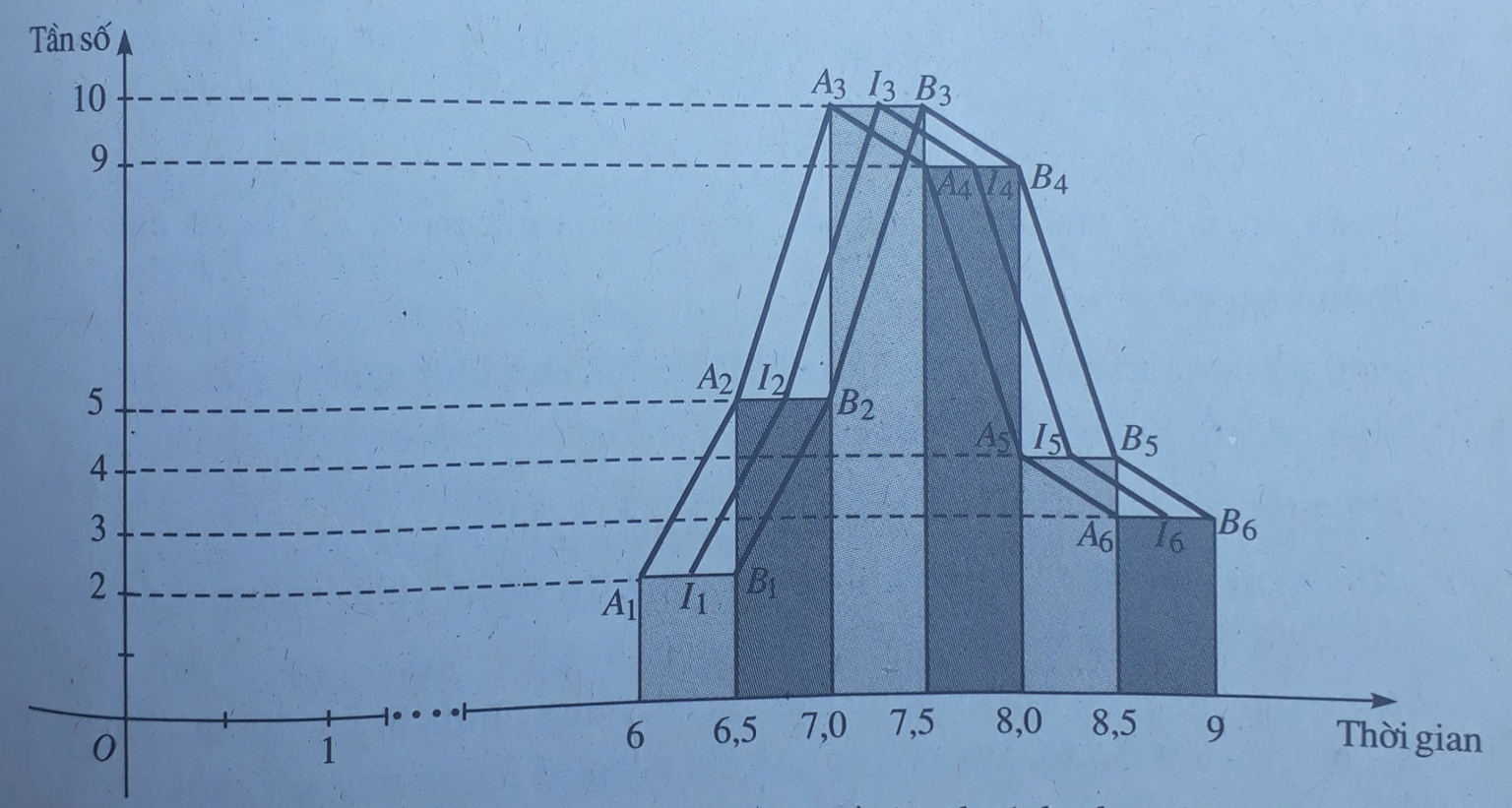
Hình 55. Biểu đồ tần số hình cột về thành tích chạy 50m của học sinh lớp 10A trường Trung học phổ thông C (đơn vị là giây)
Dựa vào biểu đồ trên, có thể vẽ được đường gấp khúc tần số (kí hiệu là D), cũng để mô tả bảng 2 và trình bày các số liệu thống kê.
Đường gấp khúc tần số D như vậy là đường gấp khúc nào dưới đây (h.55)?
Các đỉnh của đường gấp khúc tần số có tọa độ là ( c i ; n i ), với c i là giá trị đại diện của lớp thứ i, n i là tần số của lớp thứ i. Từ đó suy ra: các đỉnh của đường gấp khúc tần số là các trung điểm của các cạnh phía trên của các cột (các hình chữ nhật) của biểu đồ tần số hình cột
Đường gấp khúc I 1 I 2 I 3 I 4 I 5 I 6 với I 1 , I 2 , I 3 , I 4 , I 5 , I 6 lần lượt là trung điểm của các đoạn thẳng A 1 B 1 , A 2 B 2 , A 3 B 3 , A 4 B 4 , A 5 B 5 , A 6 B 6
Số liệu về số lớp học cấp trung học cơ sở của 5 tỉnh Tây Nguyên tính đến ngày 30/9/2021 được cho trong bảng thống kê sau:
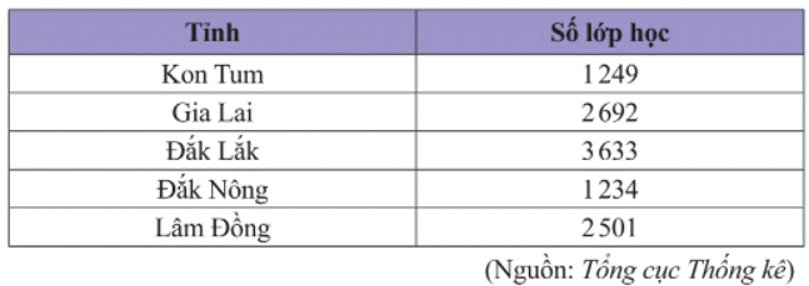
a) Số liệu từ bảng thống kê trên được biểu diễn vào biểu đồ cột như sau. Hãy tìm các giá trị của P, Q, R trong biểu đồ.
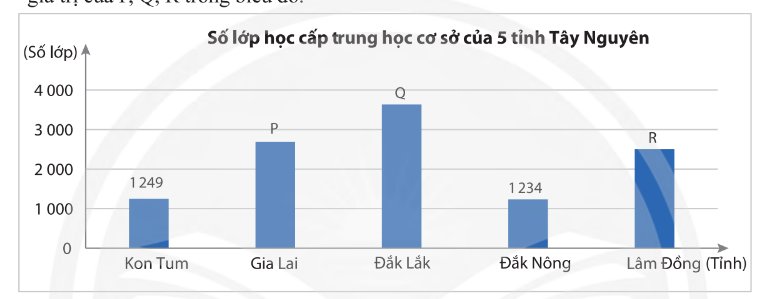
b) Biểu đồ cột ở câu a) được chuyển sang biểu đồ hình quạt tròn như dưới đây. Hãy tìm các giá trị của x, y, z, t, m trong biểu đồ.
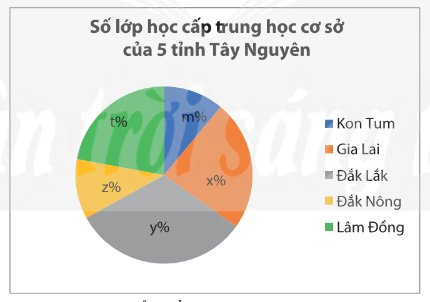
c) So sánh ý nghĩa của hai loại biểu đồ trên
a) P là số lớp học cấp trung học cơ sở của tỉnh Gia Lai nên \(P = 2692\);
Q là số lớp học cấp trung học cơ sở của tỉnh Đắk Lắk nên \(Q = 3633\);
R là số lớp học cấp trung học cơ sở của tỉnh Lâm Đồng nên \(R = 2501\).
b) Tổng số lớp học cấp trung học cơ sở của 5 tỉnh Tây Nguyên là:
\(1249 + 2692 + 3633 + 1234 + 2501 = 11309\) (lớp học).
Suy ra:
\(x\% = \frac{{2692}}{{11309}}.100\% \approx 24\% \)
\(\begin{array}{l}y\% = \frac{{3633}}{{11309}}.100\% \approx 32\% \\z\% = \frac{{1234}}{{11309}}.100\% \approx 11\% \\t\% = \frac{{2501}}{{11309}}.100\% \approx 22\% \\m\% = \frac{{1249}}{{11309}}.100\% \approx 11\% \end{array}\)
c) Biểu đồ cột cho ta thấy sự so sánh hơn kém về số lớp học cấp trung học cở sở của 5 tỉnh Tây Nguyên.
Biểu đồ hình quạt tròn ngoài việc cho ta biết sự so sánh hơn kém về số lớp học cấp trung học cơ sở của 5 tỉnh Tây Nguyên, còn cho biết tỉ lệ phần trăm số lớp học của mỗi tỉnh so với toàn thể khu vực.
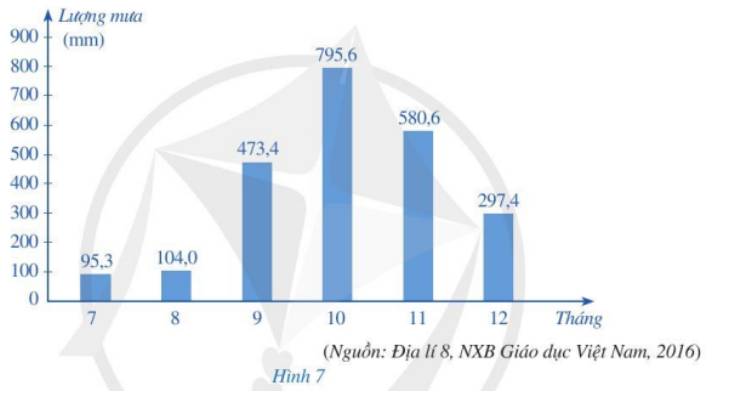
Biểu đồ ở Hình 7 biểu diễn lượng mưa tại trạm khí tượng Huế trong sáu tháng cuối năm dương lịch.
a) Nêu đối tượng thống kê và tiêu chí thống kê.
b) Lập bảng số liệu thống kê lượng mưa tại trạm khí tượng Huế theo mẫu sau:

c) Trong các tháng trên, tháng nào có lượng mưa nhiều nhất? Tháng nào có lượng mưa ít nhất?
a)
- Đối tượng thống kê là lượng mưa tại trạm khí tượng Huế.
- Tiêu chí thống kê là lượng mưa tại trạm khí tượng Huế trong sáu tháng cuối năm dương lịch.
b) Bảng số liệu thống kê lượng mưa tại trạm khí tượng Huế:
Tháng | 7 | 8 | 9 | 10 | 11 | 12 |
Lượng mưa (mm) | 95,3 | 104,0 | 473,4 | 795,6 | 580,6 | 297,4 |
c) Ta thấy:
95,3 < 104,0 < 297,4 < 473,4 < 580,6 < 795,6 (mm)
Vậy lượng mưa tại trạm khí tượng Huế vào: tháng 7 < tháng 8 < tháng 12 < tháng 9 < tháng 11 < tháng 10
Hay trong các tháng trên, tháng 10 có lượng mưa lớn nhất, tháng 7 có lượng mưa ít nhất.
Cho bảng thống kê số học sinh theo các khối lớp của một trường tiểu học:

Biểu đồ cột sau thể hiện các số liệu trên.
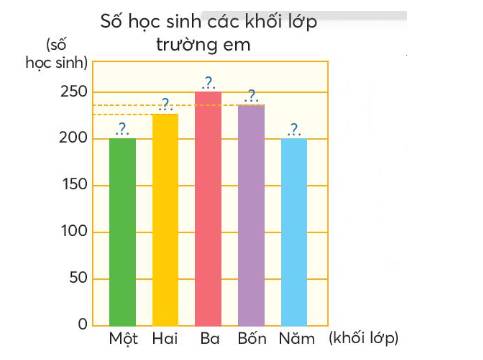
a) Biểu đồ cột ở bên biểu diễn gì?
b) Hoàn thiện biểu đồ bên.
c) Đọc số liệu trên mỗi biểu đồ rồi so sánh học sinh các khối lớp. (Dùng các từ nhiều hơn, ít hơn, bằng, nhiều nhất, ít nhất.)
d) Viết tên các khối lớp theo thứ tự số học sinh từ ít đến nhiều.
Tham khảo:
a) Biểu đồ cột ở bên biểu diễn số học sinh các khối lớp của trường em.
b)
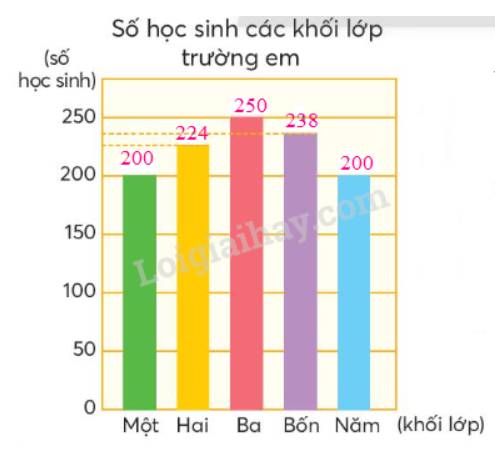
c) Số học sinh khối lớp Hai nhiều hơn số học sinh khối lớp Một.
Số học sinh khối lớp Năm ít hơn số học sinh khối lớp Ba.
....
d) Tên các khối lớp theo thứ tự số học sinh từ ít đến nhiều là: Khối Một (Khối Năm), Khối Hai, Khối Bốn, Khối Ba.
Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.
a) Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.
b) Tìm khoảng biến thiên của mẫu số liệu đó.
c) Tìm khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
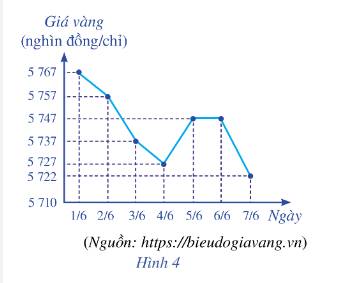
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5767 5757 5737 5727 5747 5747 5722
b) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 5767 - 5722 = 45\)
c) +) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5722 5727 5737 5747 5747 5757 5767
+) Các tứ phân vị của mẫu số liệu là:
Trung vị của mẫu số liệu: \({Q_2}\) = 5747.
Trung vị của dãy 5722 5727 5737 là: \({Q_1}\) = 5727.
Trung vị của dãy 5747 5757 5767 là: \({Q_3}\) = 5757.
+) Khoảng tứ phân vị của mẫu số liệu là: \({\Delta _Q} ={Q_3} - {Q_1}\) = 5757- 5727= 30.
d) +) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là: \(\overline x = \frac{{5722{\rm{ + }}5727{\rm{ + }}5737{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5757{\rm{ + }}5767}}{7} = 5743,43\) ( nghìn đồng/ chỉ)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5722 - \overline x } \right)}^2} + {{\left( {5727 - \overline x } \right)}^2} + ... + {{\left( {5767 - \overline x } \right)}^2}} \right]}}{7} \approx 219,39\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} = \sqrt {219,39} \approx 14,81\)( nghìn đồng/ chỉ)
Trong các loại biểu đồ (biểu đồ tranh, biểu đồ cột và biểu đồ hình quạt tròn), loại biểu đồ nào thích hợp để biểu diễn bảng số liệu thống kê bên dưới?
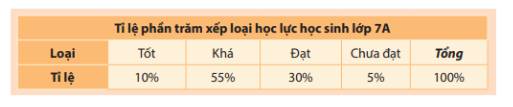
Trong các loại biểu đồ (biểu đồ tranh, biểu đồ cột và biểu đồ hình quạt tròn), biểu đồ hình quạt tròn thích hợp để biểu diễn bảng số liệu thống kê trên.