Tính nhẩm nghiệm của các phương trình:
a) \( - 315{x^2} - 27x + 342 = 0\)
b) \(2022{x^2} + 2023x + 1 = 0\)
Tính nhẩm nghiệm của các phương trình: (5 + 2 ) x 2 + (5 - 2 )x -10 =0
Phương trình (5 + 2 ) x 2 + (5 - 2 )x -10 =0 có hệ số
a =5 + 2 , b = 5 - 2 , c = -10
Ta có: a +b +c =5 + 2 +5 - 2 +(-10)=0
Suy ra nghiệm của phương trình là x 1 = 1 , x 2 = c/a = (-10)/(5+ 2 )
Tìm m để phương trình:
a) x^2 – 2mx + m + 6 = 0 có hai nghiệm phân biệt.
b) mx^2 – 2mx + m + 3 = 0 vô nghiệm.
c) (m – 2)x^2 + (2m – 3)x + m +1 = 0 có nghiệm kép
a: Ta có: \(\text{Δ}=\left(-2m\right)^2-4\cdot1\cdot\left(m+6\right)\)
\(=4m^2-4m-24\)
\(=4\left(m^2-m-6\right)\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow m^2-m-6>0\)
\(\Leftrightarrow\left(m-3\right)\left(m+2\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>3\\m< -2\end{matrix}\right.\)
b: Ta có: \(\text{Δ}=\left(-2m\right)^2-4\cdot m\cdot\left(m+3\right)\)
\(=4m^2-4m^2-12m\)
=-12m
Để phương trình vô nghiệm thì Δ<0
hay m>0
c: Ta có: \(\text{Δ}=\left(2m-3\right)^2-4\left(m-2\right)\left(m+1\right)\)
\(=4m^2-12m+9-4\left(m^2-m-2\right)\)
\(=4m^2-12m+9-4m^2+4m+8\)
\(=-8m+17\)
Để phương trình có nghiệm kép thì Δ=0
hay \(m=\dfrac{17}{8}\)
Cho phương trình 2x2 - (4m + 3)x + 2m2 - 1 = 0 . Tìm các giá trị của m để phương trình:
a) Có hai nghiệm phân biệt?
b) Có nghiệm kép; tìm nghiệm kép đó?
c) Vô nghiệm?
d) có nghiệm x = -1? Tìm nghiệm còn lại?
a: Δ=(4m+3)^2-4*2*(2m^2-1)
=16m^2+24m+9-16m^2+8
=24m+17
Để phương trình có hai nghiệm phân biệt thì 24m+17>0
=>m>-17/24
b: Để phương trìh có nghiệm kép thì 24m+17=0
=>m=-17/24
c: Để phương trình vô nghiệm thì 24m+17<0
=>m<-17/24
Dùng hệ thức Viet để tính nhẩm các nghiệm của phương trình:
a) x2 - 7x + 12 = 0; b) x2 + 7x+ 12 = 0.
a) x2 – 7x + 12 = 0 có a = 1, b = -7, c = 12
nên x1 + x2 = \(-\dfrac{-7}{1}\) = 7 = 3 + 4
x1x2 = \(\dfrac{12}{1}\) = 12 = 3 . 4
Vậy x1 = 3, x2 = 4.
b) x2 + 7x + 12 = 0 có a = 1, b = 7, c = 12
nên x1 + x2 = \(\dfrac{-7}{1}\) = -7 = -3 + (-4)
x1x2 = \(\dfrac{12}{1}\) = 12 = (-3) . (-4)
Vậy x1 = -3, x2 = -4.
a) x2 – 7x + 12 = 0 có a = 1, b = -7, c = 12
nên x1 + x2 = = 7 = 3 + 4
x1x2 = = 12 = 3 . 4
Vậy x1 = 3, x2 = 4.
b) x2 + 7x + 12 = 0 có a = 1, b = 7, c = 12
nên x1 + x2 = = -7 = -3 + (-4)
x1x2 = = 12 = (-3) . (-4)
Vậy x1 = -3, x2 = -4.
1 . Tìm giá trị của m để phương trình sau có nghiệm , sau đó tính tổnh và tích các nghiệm của phương trình đó theo m :
a ) x 2 - 4x +m = 0 ; b) x 2 - 2(m+3)x + m 2 +3 =0
2 . Nhẩm nghiệm của phương trình sau :
(m-2)x 2- ( 2m+5)x + m + 7 = 0 (m là tham số , m ≠ 2)
Giúp mình với ạ!!! Mình đang cần gấp ạ!
1,
a) \(x^2-4x+m=0\)
\(\Delta=b^2-4ac=\left(-4\right)^2-4.1.m=16-4m\)
Để pt có nghiệm : \(\Delta\ge0\)
<=>\(16-4m\ge0\)
\(\Leftrightarrow16\ge4m\)
\(\Leftrightarrow m\le4\)
tính nhẩm nghiệm của phương trình (2-√3) x^2 +2√3x- (2+√3) =0
\(a=2-\sqrt{3}\) ; \(b=2\sqrt{3}\) ; \(c=-2-\sqrt{3}\)
\(\Rightarrow a+b+c=2-\sqrt{3}+2\sqrt{3}-2-\sqrt{3}=0\)
\(\Rightarrow\) Phương trình đã cho có 2 nghiệm:
\(x_1=1\) ; \(x_2=\dfrac{c}{a}=\dfrac{-2-\sqrt{3}}{2-\sqrt{3}}=-7-4\sqrt{3}\)
Tính nhẩm nghiệm của các phương trình:
a ) 1 , 5 x 2 − 1 , 6 x + 0 , 1 = 0 b ) 3 x 2 − ( 1 − 3 ) x − 1 = 0 c ) ( 2 − 3 ) x 2 + 2 3 x − ( 2 + 3 ) = 0 d ) ( m − 1 ) x 2 − ( 2 m + 3 ) x + m + 4 = 0 v ớ i m ≠ 1.
a) 1 , 5 x 2 – 1 , 6 x + 0 , 1 = 0
Có a = 1,5; b = -1,6; c = 0,1
⇒ a + b + c = 1,5 – 1,6 + 0,1 = 0
⇒ Phương trình có hai nghiệm x 1 = 1 ; x 2 = c / a = 1 / 15 .

d) ( m – 1 ) x 2 – ( 2 m + 3 ) x + m + 4 = 0
Có a = m – 1 ; b = - (2m + 3) ; c = m + 4
⇒ a + b + c = (m – 1) – (2m + 3) + m + 4 = m -1 – 2m – 3 + m + 4 = 0
⇒ Phương trình có hai nghiệm 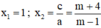
0^2020x1^2021x2^2022 x 3^2023x..x21^2120
\(0^{2020}\cdot1^{2021}\cdot....\cdot21^{2120}=0\cdot1^{2021}\cdot...\cdot21^{2120}=0\)
Bài 1: Chứng minh bất phương trình:
a) x2+2mx+2m+3>0, ∀xϵR
b) mx2+(m-1)x+m+1≤0, ∀xϵR
c) (m-1)x2+2mx+2-3m>0, vô nghiệm
Bài 2: Phương trình: mx2+(m-1)x+1-m=0
a) Có nghiệm
b) Có 2 nghiệm phân biệt
c) Có 2 nghiệm trái dấu
d) Có 2 nghiệm dương phân biệt
e) Có 2 nghiệm âm phân biệt
Bài 2:
a: TH1: m=0
=>-x+1=0
=>x=-1(nhận)
TH2: m<>0
\(\text{Δ}=\left(m-1\right)^2-4m\left(1-m\right)\)
=m^2-2m+1-4m+4m^2
=5m^2-6m+1
=(2m-1)(3m-1)
Để phương trình có nghiệm thì (2m-1)(3m-1)>=0
=>m>=1/2 hoặc m<=1/3
b: Để phương trình có hai nghiệm phân biệt thì (2m-1)(3m-1)>0
=>m>1/2 hoặc m<1/3
c: Để phương trình có hai nghiệmtrái dấu thì (1-m)*m<0
=>m(m-1)>0
=>m>1 hoặc m<0
d: Để phương trình có hai nghiệm dương phân biệt thì
\(\left\{{}\begin{matrix}m\in\left(-\infty;\dfrac{1}{3}\right)\cup\left(\dfrac{1}{2};+\infty\right)\\\dfrac{-m+1}{m}>0\\\dfrac{1-m}{m}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in\left(-\infty;\dfrac{1}{3}\right)\cup\left(\dfrac{1}{2};+\infty\right)\\0< m< 1\end{matrix}\right.\)
=>1/2<m<1
Cho hai phương trình x2+2022x+1=0 (1) và x2+2023x+1 (2).Gọi x1,x2 là nghiệm của phương trình (1) ; x3,x4 là nghiệm của phương trình (2).Giá trị của biểu thức P=(x1+x3)(x2+x3)(x1-x4)(x2-x4) là
A.4045 B.-1 C.1 D.0