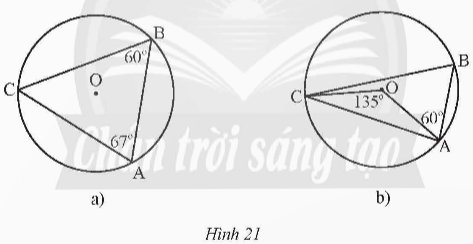
Xác định số đo các cung \(\overset\frown{AB};\overset\frown{BC};\overset\frown{CA}\) trong mỗi hình vẽ sau:
Cho ΔAOB có \(\widehat{AOB}=110^o\) . Vẽ đường tròn (O, OA). Gọi C là 1 điểm trên đường tròn (O) biết sđ \(\stackrel\frown{AC}=40^0\) . Tính số đo cung nhỏ \(\stackrel\frown{BC}\) và cung lớn \(\stackrel\frown{BC}\)
cho đường tròn tâm O đường kính AB .Vẽ góc ở tâm \(\widehat{AOC}\) =50 độ . Vẽ dây CD \(\perp\)AB và dây DE//AB
a)Tính số đo cung nhỏ BE
b)Tính số đo \(\stackrel\frown{CBE}\) từ đó suy ra 3 điểm C,O,E thẳng hàng
Tự vẽ hình
a) Do \(CD\) vuông góc \(AB\) nên \(AB\) là trung trực của \(CD\) (liên hệ giữa đường kính và dây cung)
\(\Rightarrow AC=AD\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}\)
Mà \(sđ\stackrel\frown{AC}=\stackrel\frown{AOC}=50^0\Rightarrow sđ\stackrel\frown{AD}=50^0\).
Do \(DE\) song song \(AB\)
\(sđ\stackrel\frown{BE}=sđ\stackrel\frown{AD}=50^0\Rightarrow\widehat{BOE}=sđ\stackrel\frown{BE}=50^0\).
b) Do \(B\in\stackrel\frown{CE}\Rightarrow sđ\stackrel\frown{CBE}=sđ\stackrel\frown{CB}+sđ\stackrel\frown{BE}\)
\(\Rightarrow sđ\stackrel\frown{CBE}=\widehat{COB}+\widehat{BOE}=180^0-\widehat{AOC}+\widehat{BOE}\)
\(\Rightarrow sđ\stackrel\frown{CBE}=180^0-50^0+50^0=180^0\)
\(\Rightarrow\) CE là đường kính
\(\Rightarrow\) C, O, E thẳng hàng.
Cho đương tròn (O; R) tiếp tuyến Ax. Trên tia Ax lấy điểm M sao cho AM = \(\sqrt{3}R\) , OM cắt đương tròn ở N
a, Tính số đo góc ở tâm tạo bởi 2 bán kính OA và ON
b, Tính số đo cung nhỏ \(\stackrel\frown{AN}\) và cung lớn \(\stackrel\frown{AN}\)
a) Xét ΔOAM vuông tại A có
\(\tan\widehat{AOM}=\dfrac{AM}{AO}=\sqrt{3}\cdot\dfrac{OA}{OA}=\sqrt{3}\)
hay \(\widehat{AOM}=60^0\)
\(\Leftrightarrow\widehat{AON}=60^0\)
Vậy: Số đo góc ở tâm tạo bởi 2 bán kính OA và ON là 600
b) Xét (O) có
\(\stackrel\frown{AN}\) là cung chắn góc ở tâm \(\widehat{AON}\)(gt)
nên \(sđ\stackrel\frown{AN}=60^0\)
Số đo cung lớn AN là:
\(360^0-60^0=300^0\)
cho nửa đường tròn (O) đường kính AB . Vẽ bán kính \(OC\perp AB\) . Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho \(sđ\stackrel\frown{CM}=sđ\stackrel\frown{BN}\) . CMR
a) \(\stackrel\frown{AM}=\stackrel\frown{CN}\) và AM=CN
b) MN=CA=CB
GIẢI HỘ MK CÂU B) NHA![]()
b) Do \(\stackrel\frown{AM}=\stackrel\frown{CN}\) (theo câu a) => \(\widehat{AOM}=\widehat{CON}\)
Mà \(\widehat{AOM}+\widehat{MOC}=\widehat{AOC}=90^o\) => \(\widehat{NOC}+\widehat{MOC}=\widehat{MON}=90^o\)
Xét ΔOMN và ΔOAC có: \(\widehat{MON}=\widehat{AOC}=90^o\)
OA = OM (=bán kính nửa đường tròn)
OC = ON (=bán kính nửa đường tròn)
=> ΔOMN = ΔOAC (c.g.c) => MN = AC (2 cạnh tương ứng)
CMTT => ΔOMN = ΔOBC => MN = BC (2 cạnh tương ứng)
=> MN = AC = BC
cho nửa đường tròn (O) đường kính AB . Vẽ bán kính \(OC\perp AB\) . Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho sđ\(\stackrel\frown{CM}=sđ\stackrel\frown{BN}\) . cmr :
a)cung AM = cung CN và AN=CN
b)MN=CA=CB
LÀM GIÚP MÌNH CÂU B) Ạ![]()
![]()
cho nửa đường tròn ( O) đường kính AB . Vẽ bán kính OC\(\perp\)AB . Trên cung CA và CB lần lượt lấy các điểm M và N sao cho sđ\(\stackrel\frown{CM}=sđ\stackrel\frown{BN}\). CMR
a) \(\stackrel\frown{AM}=\stackrel\frown{CN}\) và AM=CN
b) MN=CA=CB
a) Xét (O) có
M là một điểm nằm trên cung \(\stackrel\frown{CA}\)(gt)
nên \(sđ\stackrel\frown{CM}+sđ\stackrel\frown{MA}=sđ\stackrel\frown{CA}\)(1)
Xét (O) có
N là một điểm nằm trên cung \(\stackrel\frown{CB}\)(gt)
nên \(sđ\stackrel\frown{CN}+sđ\stackrel\frown{NB}=sđ\stackrel\frown{CB}\)(2)
Xét (O) có AB là đường kính(gt)
nên O là trung điểm của AB
Xét ΔCAB có
CO là đường cao ứng với cạnh AB(gt)
CO là đường trung tuyến ứng với cạnh AB(O là trung điểm của AB)
Do đó: ΔCAB cân tại C(Định lí tam giác cân)
⇒CA=CB
⇒\(sđ\stackrel\frown{CA}=sđ\stackrel\frown{CB}\)(3)
Từ (1), (2) và (3) suy ra \(sđ\stackrel\frown{CM}+sđ\stackrel\frown{AM}=sđ\stackrel\frown{CN}+sđ\stackrel\frown{NB}\)
mà \(sđ\stackrel\frown{CM}=sđ\stackrel\frown{BN}\)(gt)
nên \(sđ\stackrel\frown{AM}=sđ\stackrel\frown{CN}\)
hay \(\stackrel\frown{AM}=\stackrel\frown{CN}\)(đpcm)
Xét (O) có
AM là dây cung(A,M∈(O))
CN là dây cung(C,N∈(O))
\(\stackrel\frown{AM}=\stackrel\frown{CN}\)(cmt)
Do đó: AM=CN(Liên hệ giữa cung và dây)
Cho tam giác cân AOB có \(\widehat{AOB}\) = 120°. Vẽ đường tròn (O; OA). Gọi M là một điểm nằm trên đường tròn, biết sđ\(\stackrel\frown{AM}\) = 50°. Tính số đo cung nhỏ BM và số đo cung lớn BM.
Cho đoạn thẳng AB = 5cm . Vẽ hai cung tròn (A;3cm) và (B;4cm). Gọi C là giao điểm hai đường tròn đó. Nối A, B, C. Dùng thước đo góc xác định số đo của A C B ^ .
Trên đường tròn lượng giác, với điểm gốc A, hãy xác định các điểm M mà số đo của cung AM bằng x (rad) tương ứng đã cho ở trên và xác định sinx, cosx (lấy π ≈ 3,14)
bài 1: tìm điều kiện xác định với giá trị nào của x thì các biểu thức sau đây xác định
a, \(\sqrt{-2x+3}\)
b, \(\sqrt{3x+4}\)
c, \(\sqrt{1+x\overset{2}{ }}\)
d, \(\sqrt{^{-3}_{3x+5}}\)
e, \(\sqrt{\dfrac{2}{x}}\)
help me :((
a/ ĐKXĐ : \(-2x+3\ge0\)
\(\Leftrightarrow x\le\dfrac{3}{2}\)
b/ ĐKXĐ : \(3x+4\ge0\)
\(\Leftrightarrow x\ge-\dfrac{4}{3}\)
c/ Căn thức \(\sqrt{1+x^2}\) luôn được xác định với mọi x
d/ ĐKXĐ : \(-\dfrac{3}{3x+5}\ge0\)
\(\Leftrightarrow3x+5< 0\)
\(\Leftrightarrow x< -\dfrac{5}{3}\)
e/ ĐKXĐ : \(\dfrac{2}{x}\ge0\Leftrightarrow x>0\)
P.s : không chắc lắm á!