Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung \(\overset\frown{BD};\overset\frown{BE};\overset\frown{EC}\).

Những câu hỏi liên quan
Cho tam giác ABC đều, vẽ đường tròn đường kính BC cắt cạnh AB và AC tại D và E. So sánh các cung sau BD, DE, EC
nối BE , CD
=> \(\widehat{BEC}=90,\widehat{CDB}=90\)
MÀ \(\widehat{ACB}=\widehat{ABC}=60\)
=>\(\widehat{CBE}=\widehat{BCD}=90-60=30\)
=> CUNG CE = CUNG BD
VÌ TAM GIÁC ĐỀU => CE VỪA LÀ ĐƯỜNG CAO CŨNG LÀ PHÂN GIÁC => CUNG BD = CUNG DE
Đúng 0
Bình luận (0)
Cho tam giác ABC đều . Vẽ nửa đường tròn o đg kính BC ra phía ngoài tam giác ABC gọi D,E là 2 điểm thuộc nửa đg tròn sao cho cung BD = cung DE = cung EC , AD và AE cắt BC lần lượt tại M vàN . Cm a, tam giác ABN đồng dạng vs tam giác ECN b, BM = MN = NC
Xem chi tiết
a) Gọi O là trung điểm của BC.
Ta có \(\stackrel\frown{BD}=\stackrel\frown{DE}=\stackrel\frown{EC}\Rightarrow\widehat{BOD}=\widehat{DOE}=\widehat{EOC}=60^o\).
Từ đó CE // AB, BD // AC.
Suy ra \(\Delta ABN\sim\Delta ECN\).
b) Theo tính đối xứng ta có BM = CN.
Ta có \(\dfrac{BN}{NC}=\dfrac{AB}{CE}=\dfrac{AB}{CO}=2\Rightarrow BN=2NC\Rightarrow MN=NC\).
Dễ dàng suy ra đpcm.
Đúng 0
Bình luận (0)
Cho tam giác đều ABC. Vẽ đường tròn tâm O, đường kính BC cắt AB và AC lần lượt tại D và E
a)So sánh DE và BC
b)Tam giác OBD là tam giác gì?vì sao?
c)Chứng Minh: DE//BC
cho tam giác ABC nhọn. Vẽ đường tròn tâm O dường kính BC cắt 2 cạnh AB,AC lần lượt tại E và D; BD và CE cắt nhau tại H
a,chứng minh rằng: H vuông góc với BC
b,chứng minh: bốn điểm A,H,E,D cùng thuộc 1 đường tròn và DE<BC
c,gọi M,N lần lượt chân các đường vuông góc kẻ từ B và C đến DE. Chứng minh rằng ME=ND
a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC
Đúng 0
Bình luận (0)
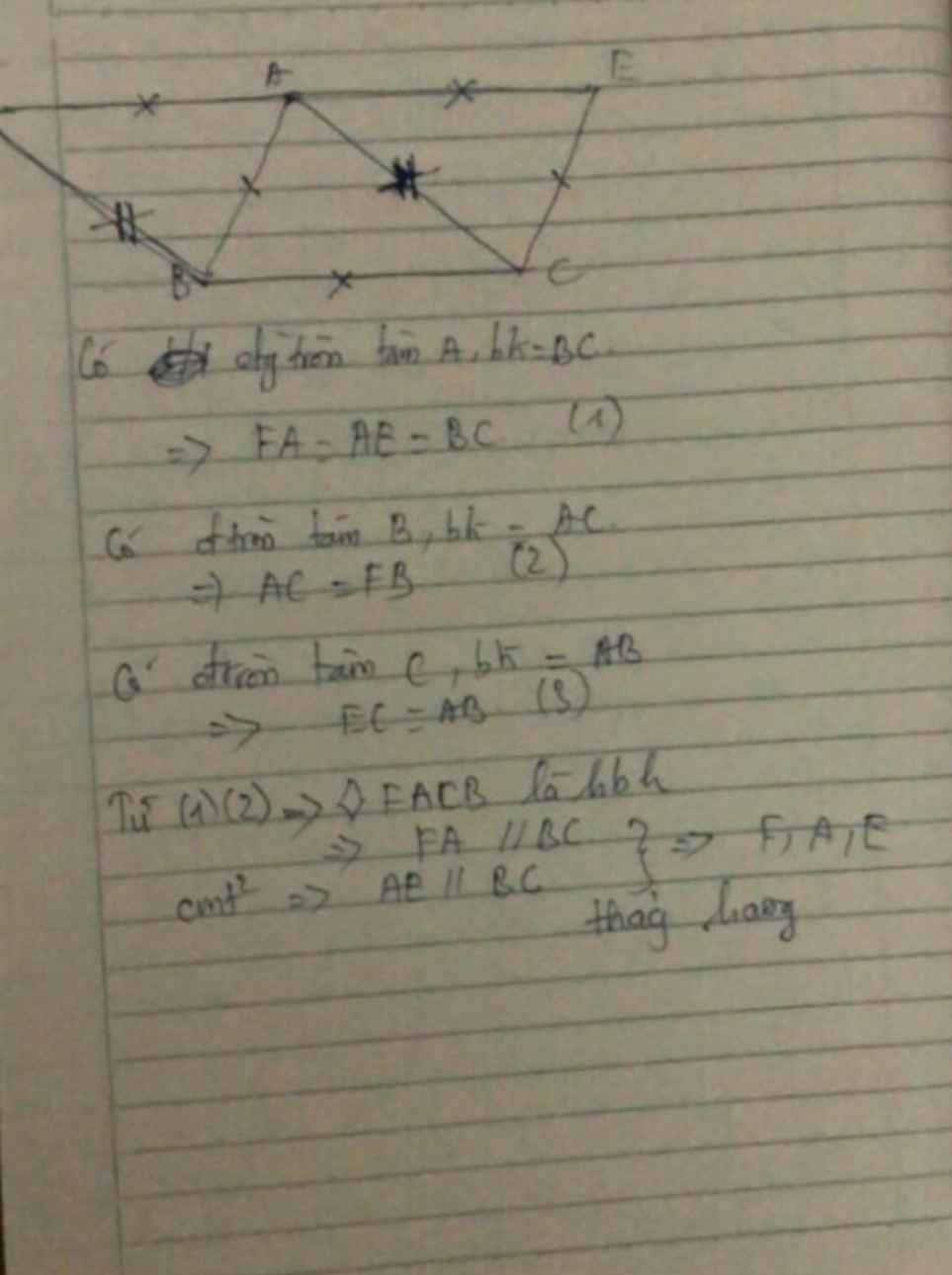
Cho tam giác ABC. Vẽ cung tròn tâm C bán kính AB và cung tròn tâm B bán kính AC. Đường tròn tâm A bán kính BC cắt các cung tròn tâm C và tâm B lần lượt tại E và F. ( E và F nằm trên cùng nửa mặt phẳng bờ BC chứa A)
Chứng minh ba điểm F, A, E thẳng hàng.
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.
Đọc tiếp
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.
4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.

Vì N là điểm chính giữa cung nhỏ BC nên DN là trung trực của BC nên DN là phân giác B D C ^
Ta có K Q C ^ = 2 K M C ^ (góc nọi tiếp bằng nửa góc ở tâm trong dường tròn (Q))
N D C ^ = K M C ^ (góc nội tiếp cùng chắn cung N C ⏜ )
Mà B D C ^ = 2 N D C ^ ⇒ K Q C ^ = B D C ^
Xét 2 tam giác BDC & KQC là các các tam giác vuông tại D và Q có hai góc ở ⇒ B C D ^ = B C Q ^ do vậy D, Q, C thẳng hàng nên KQ//PK
Chứng minh tương tự ta có ta có D, P, B thẳng hàng và DQ//PK
Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng (điều phải chứng minh).
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn, vẽ đường tròn đường kính BC=2R cắt các cạnh AB và AC lần lượt tại D và E. BD và CE cắt nhau tại H. Tia AH cắt BC tại F. a) cm tứ giác ADHE nội tiếp
b) Gọi I là giao điểm của BE và DF. Chứng minh IH.BE=BI.HE
Cho tam giác ABC có AB > AC .Trên cạnh AB lấy điểm D sao cho AD = AC đường tròn tâm O ngoại tiếp tam giác BCD .Từ O lần lượt hạ các đường vuông góc OH,OK xuống BC và BD (H ∈ BC , K ∈ BD). So sánh hai cung nhỏ BD và BC
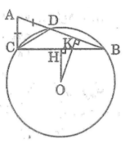
Theo câu a ,BC > BD
Vì trong một đường tròn, dây cung lớn hơn căng cung lớn hơn nên :
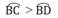
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn (AB < AC) .Vẽ đường tròn (O; R) đường kính BC cắt hai cạnh AB, AC lần lượt tại E và D.Gọi H là giao điểm của BD và CE. a) Chứng minh: góc BEC = 90° và tứ giác AEHD nội tiếp b) Tia DE cắt đường thẳng BC tại S. Chứng minh: AH vuông góc BC và SE .SD=SB.SC c)Tia AH cắt BC tại F. Chứng minh: FEC =FAC và tứ giác OFED nội tiếp và OF.OS = R²
a: góc BEC=1/2*180=90 độ
góc BDC=1/2*180=90 độ
góc AEH+góc ADH=180độ
=>AEHD nội tiếp
b: Xet ΔABC có BD,CE là đường cao
BD cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC
Xét ΔSBE và ΔSDC co
góc SBE=góc SDC
góc S chung
=>ΔSBE đồng dạngvơi ΔSDC
=>SB/SD=SE/SC
=>SB*SC=SD*SE
c: góc AFC=góc AEC=90 độ
=>AEFC nội tiếp
=>góc FEC=góc FAC
Đúng 1
Bình luận (0)
Bài 1: Cho nửa đường tròn (O) đường kính AB và dây cung AC. N là điểm chính giữa của cung CB. Chưng minh AN là tia phân giác của góc CABBài 2: Cho tam giác ABC nhọn nối tiếp đường trnf (O) đường kính BD. Biết góc BAC bằng 45 độ. Tính số đo góc CBD Bài 3 cho tam giác ABC nhọn có góc BAC 60 độ. vẽ đường tròn đường kính BC tâm O cắt AB, AC lần lượt tại D và E. tính số đo góc ODEgiúp mình với mình đang cần gấp :((
Đọc tiếp
Bài 1: Cho nửa đường tròn (O) đường kính AB và dây cung AC. N là điểm chính giữa của cung CB. Chưng minh AN là tia phân giác của góc CAB
Bài 2: Cho tam giác ABC nhọn nối tiếp đường trnf (O) đường kính BD. Biết góc BAC bằng 45 độ. Tính số đo góc CBD
Bài 3 cho tam giác ABC nhọn có góc BAC= 60 độ. vẽ đường tròn đường kính BC tâm O cắt AB, AC lần lượt tại D và E. tính số đo góc ODE
giúp mình với mình đang cần gấp :((