Giáo viên ghi lại thời gian chạy cự li 100 mét của các học sinh lớp 9A cho kết quả như sau:

a) Nêu các nhóm số liệu và tần số tương ứng.
b) Lập bảng tần số tương đối ghép nhóm.
Thời gian chạy 50m của nhóm số 1 lớp 9D được thầy giáo ghi lại trong bảng sau:
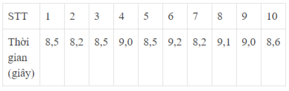
Tần số tương ứng của giá trị 8,5 là:
A. 1
B. 2
C. 3
D. 4
Quan sát bảng ta thấy tần số tương ứng của giá trị 8,5 là 3
Chọn đáp án C
Anh Văn ghi lại cự li 30 lần ném lao của mình ở bảng sau (đơn vị: mét):

a) Tính cự li trung bình của mỗi lần ném.
b) Tổng hợp lại kết quả ném của anh Văn vào bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng cự li trung bình mỗi lần ném từ bảng tần số ghép nhóm trên.
d) Khả năng anh Văn ném được khoảng bao nhiêu mét là cao nhất?
a) Cự li trung bình của mỗi lần ném là: \(\bar x = 71,6\left( m \right)\).
b)

c)
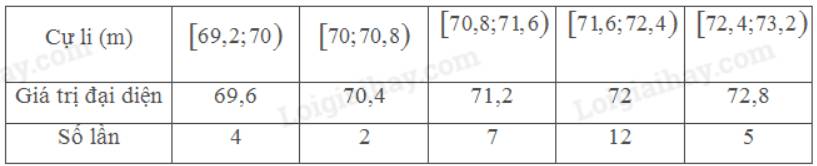
Cự li trung bình mỗi lần ném sau khi ghép nhóm là:
\(\bar x = \frac{{4.69,6 + 2.70,4 + 7.71,2 + 12.72 + 72,8.5}}{{30}} = 71,52\left( m \right)\)
d) Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {71,6;72,4} \right)\).
Do đó: \({u_m} = 71,6;{n_{m - 1}} = 7;{n_m} = 12;{n_{m + 1}} = 5;{u_{m + 1}} - {u_m} = 72,4 - 71,6 = 0,8\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 71,6 + \frac{{12 - 7}}{{\left( {12 - 7} \right) + \left( {12 - 5} \right)}}.0,8 \approx 71,9\left( m \right)\)
Vậy khả năng anh Văn ném được khoảng 71,9 mét là cao nhất.
Bài 1: Theo dõi thời gian làm bài một bài toán (tính bằng phút) của một nhóm học sinh. Thầy giáo ghi lại như sau:
3 | 5 | 7 | 2 | 4 | 7 | 8 | 9 |
7 | 8 | 6 | 7 | 5 | 3 | 8 | 7 |
5 | 4 | 8 | 7 | 7 | 9 | 4 | 7 |
5 | 3 | 9 | 7 | 7 | 4 | 7 | 6 |
a. Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b. Hãy lập bảng tần số
Dấu hiệu là thời gian làm bài toán của 1 nhóm hsinh
Có 28GT
| GT(x) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| Tần số(n) | 1 | 3 | 4 | 4 | 1 | 9 | 4 | 2 | (Thừa) | (Thừa) | N=28 |
a dấu hiệu (X) là thời gian làm một bài toán (tính bằng phút) của mỗi học sinh
số các giá trị là 32
b mạng yếu ko kẻ được nên viết thôi nha
giá trị (x) 2 3 4 5 6 7 8 9
tần số (n) 1 3 4 4 2 11 4 3 N=32
Dấu hiệu ở đây là thời gian làm bài một bài toán (tính bằng phút) của một nhóm học sinh
Số các giá trị là 32
| Điểm | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Tần số | 1 | 3 | 4 | 4 | 2 | 11 | 4 | 3 |
Cho các số liệu thống kê được ghi trong hai bảng sau
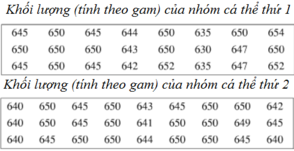
a) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là
[630; 635) ; [635;640) ; [640; 645) ; [645; 650) ; [650; 655)
b) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 2 với các lớp là:
[638;642) ; [642; 646) ; [646;650) ; [650; 654] ;
c) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu a) bằng cách vẽ biểu đồ tần suất hình cột và đường gấp khúc tần suất
d) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu b) bằng cách vẽ biểu đồ tần số hình cột và đường gấp khúc tần số
e) Tính số trung bình cộng, phương sai và độ lệch chuẩn của các bảng phân bố đã lập được
Từ đó, xét xem nhóm cá nào có khối lượng đồng đều hơn
a) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [630;635) | 1 | 4,2% |
| [635;640) | 2 | 8,3% |
| [640;645) | 3 | 12,5% |
| [645;650) | 6 | 25% |
| [650;655] | 12 | 50% |
| Cộng | 24 | 100% |
b) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [638;642) | 5 | 18,52% |
| [642;646) | 9 | 33,33% |
| [646;650) | 1 | 3,7% |
| [650;654) | 12 | 44,45% |
| Cộng | 27 | 100% |
c) Biểu đồ tần suất hình cột:
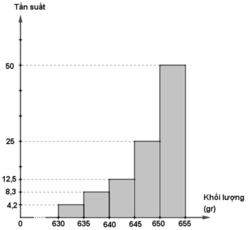
- Đường gấp khúc tần suất
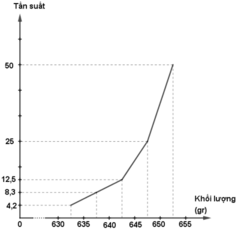
d) Biểu đồ tần số
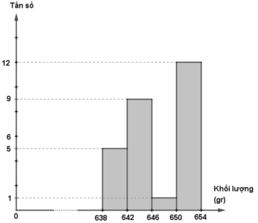
- Đường gấp khúc tần số
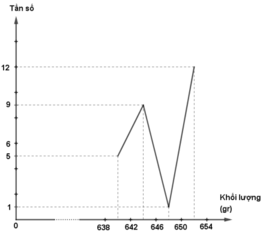
e) * Xét bảng phân bố ở câu a)
- Số trung bình:
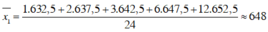
- Phương sai:
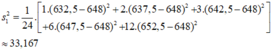
- Độ lệch chuẩn:
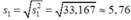
* Xét bảng phân bố ở câu b):
- Số trung bình:
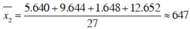
- Phương sai:
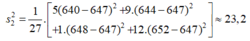
- Độ lệch chuẩn:
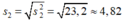
Nhận thấy s2 < s1 nên nhóm cá thứ hai có khối lượng đồng đều hơn.
Một giáo viên dạy Giáo dục thể chất đã thống kê thời gian chạy 100 m (tính theo giây) của 20 học sinh nam và ghi lại trong bảng số liệu ban đầu như sau:

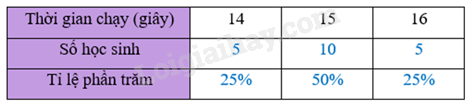
a) Chuyển dữ liệu từ bảng số liệu ban đầu ở trên sang dạng bảng thống kê sau đây:

b) Hãy chuyển dữ liệu từ bảng thống kê ở câu a sang dạng biểu đồ cột và biểu đồ hình quạt tròn sau đây:
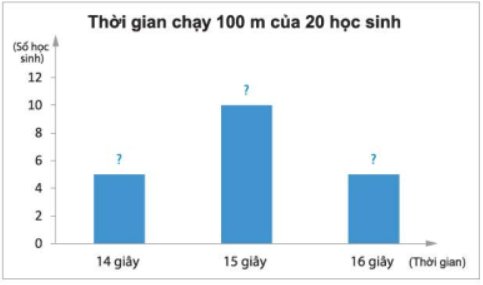
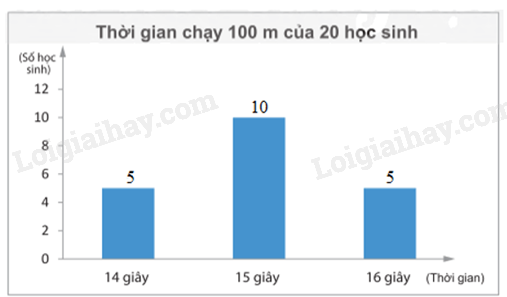
Biểu đồ cột:
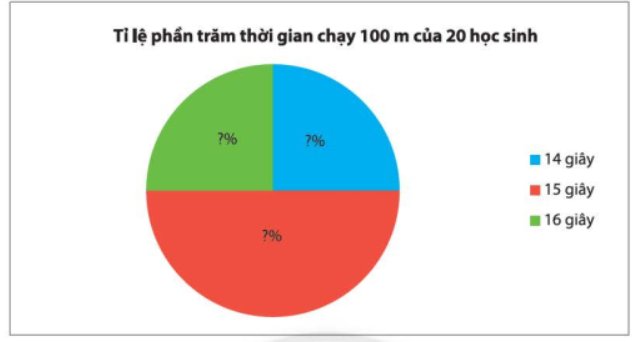
Biểu đồ hình quạt tròn:
a) Chuyển dữ liệu từ bảng số liệu ban đầu ở trên sang dạng bảng thống kê sau đây:
b) Biểu đồ cột biểu diễn thời gian chạy 100 m (tính theo giây) của 20 học sinh nam:
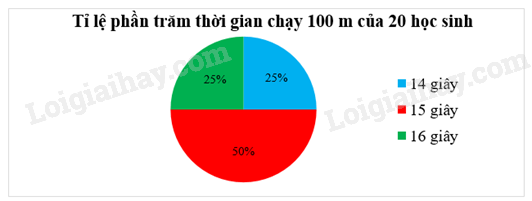
Biểu đồ hình quạt tròn biểu diễn thời gian chạy 100 m (tính theo giây) của 20 học sinh nam:
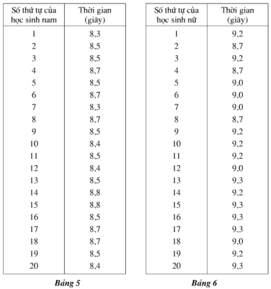
Thời gian chạy 50m của các học sinh trong một lớp 7 được thầy giáo dạy Thể dục ghi lại trong hai bảng 5 và 6.
Hãy cho biết:
Các giá trị khác nhau của dấu hiệu và tần số của chúng (đối với từng bảng)
| Bảng 5 | Bảng 6 |
|---|---|
| Giá trị 8,3 có tần số 2 Giá trị 8,4 có tần số 3 Giá trị 8,5 có tần số 8 Giá trị 8,7 có tần số 5 Giá trị 8,8 có tần số 2 |
Giá trị 8,7 có tần số 3 Giá trị 9,0 có tần số 5 Giá trị 9,2 có tần số 7 Giá trị 9,3 có tần số 5 |
Một giáo viên thể dục đo chiều cao (tính theo cm) của một nhóm học sinh nữ và ghi lại ở bảng sau:
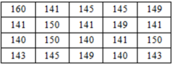
Lập bảng tần số:
A. 
B. 
C. 
D. 
Tuổi các học viên của một lớp học Tiếng Anh tại một trung tâm được ghi lại ở bảng tần số ghép lớp như sau:
Lớp |
Tần số |
[16; 20) [20; 24) [24; 28) [28; 32) [32; 36) |
10 12 14 9 5 |
Khi đó độ lệch chuẩn của bảng số liệu là (kết quả làm tròn đến hàng phần chục):
A. 24,8
B. 5,3
C. 5,0
D. 25,0
Cách 1:
+ Giá trị đại diện mỗi lớp: c 1 = 18 ; c 2 = 22 ; c 3 = 26 ; c 4 = 30 ; c 5 = 34
+ Số trung bình cộng:
x = n 1 c 1 + n 2 c 2 + n 3 c 3 + n 4 c 4 + n 5 c 5 n 1 + n 2 + n 3 + n 4 + n 5 = 10 . 18 + 12 . 22 + 14 . 26 + 9 . 30 + 5 . 34 50 ≈ 25
+ Độ lệch chuẩn:
s = s 2 = 10 18 - 25 2 + 12 22 - 25 2 + 14 26 - 25 2 + 9 30 - 25 2 + 5 34 - 25 2 50
≈ 5 , 0
Cách 2: Sử dụng máy tính Casio fx - 570 VNPLUS
+ Nhập ![]() (vào chế thống kê).
(vào chế thống kê).
+ Nhập ![]() (hiển thị cột tần số).
(hiển thị cột tần số).
+ Nhập ![]() (nhập giá trị).
(nhập giá trị).
+ Nhập ![]() (nhập tần số), sau đó ấn
(nhập tần số), sau đó ấn ![]() .
.
+ Nhập ![]()
⇒ δ x = 4 , 983813801
(Lưu ý: Đối với Ví dụ 2, phương sai s 2 = 24 , 9 ).
Đáp án C.
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)
Thời gian chạy 50m của nhóm số 1 lớp 9D được thầy giáo ghi lại trong bảng sau:
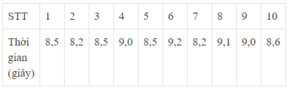
Giá trị có tần số lớn nhất là:
A. 8,2
B. 8,5
C. 8,6
D. 9,0
Tần số tương ứng với các giá trị 8,2; 8,5; 8,6; 9,0 là 1; 3; 1; 2
Vậy giá trị có tần số lớn nhất là 8,5
Chọn đáp án B