Dựa vào đề bài, viết phương trình ẩn x thu được và giải phương trình này để tìm x. Từ đó, trả lời câu hỏi trong tình huống mở đầu.

Những câu hỏi liên quan
Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hoà loại hai chiều và một chiều mà cửa hàng cần nhập. Từ HĐ1, viết hệ bất phương trình hai ẩn x, y và chỉ ra một nghiệm của hệ này.
- Lập hệ:
Do số lượng máy nhập vào phải là số tự nhiên nên ta có \(x \ge 0,y \ge 0\).
Từ HĐ 1 ta có hai bất phương trình là \(x + y \le 100\) và \(2x + y \le 120\)
Vậy hệ bất phương trình từ HĐ 1 là
\(\left\{ \begin{array}{l}x + y \le 100\\2x + y \le 120\\x \ge 0\\y \ge 0\end{array} \right.\).
Cặp số (x;y)=(50;10) là một nghiệm của hệ BPT vì thay x= 50, y= 10 ta được:
\(\left\{ {\begin{array}{*{20}{l}}
{50 + 10 \le 100}\, \text {(Đúng)}\\
{2.50 + 10 \le 120}\, \text {(Đúng)}\\
{50 \ge 0}\, \text {(Đúng)}\\
{10 \ge 0}\, \text {(Đúng)}
\end{array}} \right.\)
Đúng 0
Bình luận (0)
Cặp số (x; y) = (100; 100) thoả mãn bất phương trình bậc nhất hai ẩn nào trong hai bất phương trình thu được ở HĐ1? Từ đó cho biết rạp chiếu phim có phải bù lỗ hay không nếu bán được 100 vé loại 1 và 100 vé loại 2.
Trả lời câu hỏi tương tự với cặp số (x; y) = (150; 150).
Bước 1:
Từ HĐ 1 ta có hai bất phương trình:
\(x + 2y \ge 400\left( 1 \right)\) và \(x + 2y < 400\left( 2 \right)\)
Thay x=100 và y=100 vào bất phương trình (1) ta được:
\(100 + 2.100 \ge 400 \Leftrightarrow 300 \ge 400\) (Vô lí)
=> Cặp số (x;y)=(100;100) không thỏa mãn bất phương trình (1).
Thay x=100 và y=100 vào bất phương trình (2) ta được:
\(100 + 2.100 < 400 \Leftrightarrow 300 < 400\) (Đúng)
=> Cặp số (x;y)=(100;100) thỏa mãn bất phương trình (2).
Cặp số (x;y)=(100;100) thỏa mãn bất phương trình (2) có nghĩa là nếu bán được 100 vé loại 1 và 100 vé loại 2 thì rạp chiếu phim phải bù lỗ.
Bước 2:
Thay x=150 và y=150 vào bất phương trình (1) ta được:
\(150 + 2.150 \ge 400 \Leftrightarrow 450 \ge 400\) (Đúng)
=> Cặp số (x;y)=(150;150) thỏa mãn bất phương trình (1).
Thay x=150 và y=150 vào bất phương trình (2) ta được:
\(150 + 2.150 < 400 \Leftrightarrow 450 < 400\) (Vô lí)
=> Cặp số (x;y)=(150;150) không thỏa mãn bất phương trình (2).
Cặp số (x;y)=(150;150) thỏa mãn bất phương trình (1) có nghĩa là nếu bán được 150 vé loại 1 và 150 vé loại 2 thì rạp chiếu phim không phải bù lỗ.
Chú ý
Khi thay cặp số (x;y)=(100;100) vào các bất phương trình bài cho đồng nghĩa với rạp chiếu phim bán được 100 vé loại 1 và 100 vé loại 2.
Đúng 0
Bình luận (0)
Giải hệ hai phương trình thu được trong câu hỏi 3 và câu hỏi 4 rồi trả lời bài toán.
Từ ?3 và ?4 ta có hệ phương trình
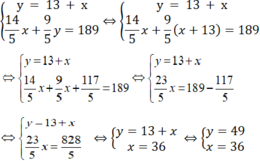
Vậy vận tốc của xe tải là 36 km/h
Vận tốc của xe khách là 49 km/h
Đúng 0
Bình luận (0)
Giải hệ hai phương trình thu được trong câu hỏi 3 và câu hỏi 4 rồi trả lời bài toán.
Từ ?3 và ?4 ta có hệ phương trình
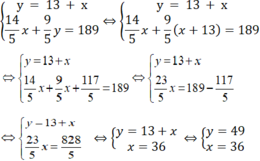
Vậy vận tốc của xe tải là 36 km/h
Vận tốc của xe khách là 49 km/h
Đúng 0
Bình luận (0)
Câu hỏi 11 (1.5 điểm) Bài 2: (1,5đ) Cho phương trình ẩn x : (1) a) Giải phương trình (1) với m = 3 b) Tìm m để phương trình (1) luôn có nghiệm ?
Cho hình dưới. Hãy viết một phương trình để từ đó có thể tìm được x (không phải giải phương trình này).
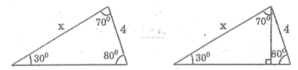
Từ đỉnh của góc 70 ° , kẻ đường cao của tam giác.
Sử dụng tỉ số sin của các góc, ta có phương trình: xsin 30 ° = 4sin 80 °
Đúng 0
Bình luận (0)
Xét tình huống mở đầu.
a) Giải bài toán ở tình huống mở đầu
b) Biết rằng quá trình hít vào xảy ra khi v > 0 và quá trình thở ra khi v < 0. Trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm nào thì người đó hít vào? Người đó thở ra?
a) Chu ký hô hấp: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{\pi }{3}}} = 6\left( s \right)\)
Số chu kỳ hô hấp trong 1 phút là \(\frac{60}{6}=10\)(chu kì).
b) Ta có: \(v=0,85\sin \frac{\pi t}{3}\)
+) v > 0 khi \(0,85\sin \frac{\pi t}{3}>0\Leftrightarrow \sin \frac{\pi t}{3}>0\)
Mà – 1 ≤ \(\frac{\pi t}{3}\)≤ 1 với mọi x ∈ ℝ. Do đó, \(0<\sin \frac{\pi t}{3}\le 1\).
+) v < 0 khi \(0,85\sin \frac{\pi t}{3}<0\Leftrightarrow \sin \frac{\pi t}{3}<0\).
Mà – 1 ≤ \(\frac{\pi t}{3}\)≤ 1 với mọi x ∈ ℝ. Do đó, −1 ≤ sin\(\frac{\pi t}{3}\) < 0.
+) Với t ∈ (0; 3) ta có 0 < sin\(\frac{\pi t}{3}\) ≤ 1.
+) Với t ∈ (3; 5] ta có −1 ≤ sin\(\frac{\pi t}{3}\) < 0.
Vậy trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm sau 0 giây đến trước 3 giây thì người đó hít vào và khoảng thời điểm sau 3 giây đến 5 giây thì người đó thở ra.
Đúng 0
Bình luận (0)
Đọc văn bản sau và trả lời câu hỏi:
a) Trong văn bản trên, đâu là phần Thân bài? Ở phần này, người viết đã trình bày những nhận xét gì về tình yêu quê hương trong bài thơ Quê hương? Những suy nghĩ, ý kiến ấy được dẫn dắt, khẳng định bằng cách nào, được liên kết với phần Mở bài và Kết bài ra sao?
a.
Thân bài (từ "Nhà thơ đã viết về…" cho đến "…thành thực của Tế Hanh."): Trình bày những cảm nhận, phân tích về tình yêu quê hương tha thiết, trong sáng, thơ mộng của nhà thơ qua bức tranh dân chài ra khơi và cảnh trở về bến cùng những hình ảnh đặc sắc thể hiện nỗi nhớ, tình thương của tác giả.
Các luận điểm chính của phần Thân bài:
+ Nhận định khái quát: Nhà thơ đã viết về Quê hương bằng tất cả tình yêu tha thiết, trong sáng, đầy thơ mộng của mình.
+ Cảnh ra khơi đánh cá của trai làng một sớm mai đẹp như mơ.
+ Cảnh đón thuyền đánh cá trở về ồn ào, tấp nập, no ấm, yên bình.
+ Hình ảnh người dân chài được khắc hoạ nổi bật giữa đất trời lộng gió với hình khối, màu sắc và cả hương vị không thể lẫn.
+ Những kỉ niệm ám ảnh, vẫy gọi.
Các luận điểm chính của phần Thân bài:
+ Nhận định khái quát: Nhà thơ đã viết về Quê hương bằng tất cả tình yêu tha thiết, trong sáng, đầy thơ mộng của mình.
+ Cảnh ra khơi đánh cá của trai làng một sớm mai đẹp như mơ.
+ Cảnh đón thuyền đánh cá trở về ồn ào, tấp nập, no ấm, yên bình.
+ Hình ảnh người dân chài được khắc hoạ nổi bật giữa đất trời lộng gió với hình khối, màu sắc và cả hương vị không thể lẫn.
+ Những kỉ niệm ám ảnh, vẫy gọi.
Giữa Mở bài, Thân bài và Kết bài có mối liên kết chặt chẽ cả về nội dung lẫn hình thức.
Đúng 0
Bình luận (0)
Hoạt động 1
Trong bài toán ở phần mở đầu, giả sử
a) Viết phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lũy thừa?
a) Phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu là:
\(S=2S.e^{1,14.t}\Leftrightarrow2e^{1,14t}=1\Leftrightarrow e^{1,14t}=\dfrac{1}{2}\)
b) Phương trình vừa tìm được có ẩn là t và nằm ở vị trí mũ của lũy thừa
Đúng 1
Bình luận (0)
Lực có gây ra tác dụng làm quay vật không nếu có phương song song với trục quay? Dựa vào tình huống trong Hình 14.4 để minh họa cho câu trả lời của em.
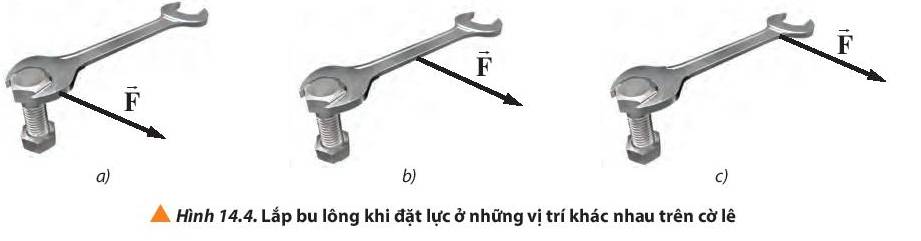
Lực không gây ra tác dụng làm quay vật nếu lực có phương song song với trục quay.
Trong Hình 14.4, lực có phương vuông góc với trục quay mới có tác dụng làm quay vật.
Đúng 0
Bình luận (0)














