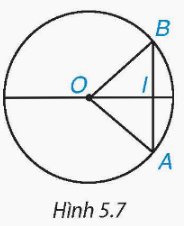
Xét dây AB tùy ý không đi qua tâm của đường tròn (O; R) (H.5.7). Dựa vào quan hệ giữa các cạnh của tam giác AOB, chứng minh AB < 2R.
Cho ba điểm cố định thẳng hàng A,M,B theo thứ tự đó.Vẽ 1 đường tròn tùy ý có tâm là O nhận AB làm dây không đi qua tâm. Gọi H là hình chiếu của M lên OA,tia đối của tia MH cắt đường tròn (O) tại N,chứng minh: độ dài AN luôn không đổi.
Cho ba điểm cố định thẳng hàng A,M,B theo thứ tự đó.Vẽ 1 đường tròn tùy ý có tâm là O nhận AB làm dây không đi qua tâm. Gọi H là hình chiếu của M lên OA,tia đối của tia MH cắt đường tròn (O) tại N,chứng minh: độ dài AN luôn không đổi.
Kéo dài AO cắt đường tròn (O) tại J, từ đó suy ra AJ là đường kính hay \(\widehat{ABJ}=\widehat{ANJ}=90^o\) .
Ta thấy ngay \(\Delta AMH\sim\Delta AJB\left(g-g\right)\Rightarrow\frac{AH}{AB}=\frac{AM}{AJ}\Rightarrow AH.AJ=AB.AM\) (không đổi).
Xét tam giác vuông ANJ, áp dụng hệ thức lượng ta có: \(AN^2=AH.AJ=AM.AB\) (không đổi)
Vậy AN luôn không đổi và \(AN=\sqrt{AM.AB}\).
Cho đường tròn tâm O và dây AB cố định, điểm M tùy ý thay đổi trên đoạn AB. Qua A và M dựng đường tròn tâm I tiếp xúc đường tròn tâm O tại A. Qua B và M dựng đường tròn tâm J tiếp xúc đường tròn tâm O tại B. 2 đường tròn tâm I và đường tròn tâm J cắt nhau tại điểm thứ 2 là N. CMR MN luôn đi qua 1 điểm cố định
Cho đường tròn (O) và dây AB cố dịnh, điểm M tùy ý thay đổi trên đoạn thẳng AB. Qua A , M dựng đường tròn tâm I tiếp xúc với đường tròn (O) tại A. Qua B và M dựng đường tròn tâm J tiếp xúc với (O) tại B. Hai đường tròn tâm I và tâm J cắt nhau tại điểm thứ hai N. Chứng minh rằng MN luôn đi qua một điểm cố định.

(hình mình lấy bên pitago coi như là gợi ý luôn)
Cho đường tròn tâm O.Gọi I là điểm chính giữa của cung AB (không phải là cung nửa đường tròn) và H là trung điểm của dây AB .Chứng minh rằng đường thẳng IH đi qua tâm O của đường tròn
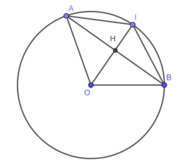
Suy ra : IA =IB (hai cung bằng nhau căng hai dây bằng nhau)
Hay I nằm trên đường trung trực của AB
Mà OA =OB (=R)
Nên O nằm trên đường trung trực của AB
Suy ra OI là đường trung trực của AB
Vì H là trung điểm của AB nên OI đi qua trung điểm H
Vậy ba điểm I, H, O thẳng hàng
Cho đường tròn tâm O, đường kính AB cố định. Qua I là điểm cố định thuộc đoạn OA (I không trùng A và O) vẽ đường thẳng vuông góc với AB cắt đường tròn tâm O tại M và N. Gọi C là điểm tùy ý thuộc cung lớn MN (C không trùng các điểm M, N và B), E I là giao điểm của AC và MN.
1) Chứng minh tứ giác IECB nội tiếp đường tròn.
2) Chứng minh AE.AC = AI.AB.
3) Chứng minh khi điểm C thay đổi trên cùng lớn MN của đường tròn tâm O thì tầmđường tròn ngoại tiếp tam giác CME luôn thuộc một đường thẳng cố định.
Cho nửa đường tròn tâm O đường kính AB=2R. Gọi C là 1 điểm tùy ý trên nửa đường tròn (O) sao cho AC>BC (A, B khác C). Qua O kẻ đường thẳng vuông góc với AB cắt dây AC tại D. a) Chứng minh tứ giác BCDO nội tiếp b) Chứng minh AD.AC=AO.AB c) Vẽ tiếp tuyến tại C của đường tròn (O). Từ D vẽ đường thẳng song song với AB cắt tiếp tuyến này tại E. Chứng minh AD//OE.
cho đường tròn tâm O dây AB không đi qua tâm ,N và M là điểm chính giữa cung AB lớn và nhỏ.
a)Chứng minh MN là đường trung trực của dây AB
b)Chứng minh3 điểm M,O,N thẳng hàng
Cho đường tròn (O). Gọi I là điểm chính giữa của cung AB (không phải là cung nửa đường tròn) và H là trung điểm của dây AB. Chứng minh rằng đường thẳng IH đi qua tâm O của đường tròn ?
Vì I là điểm chính giữa của cung AB nên IA=IB
=>I nằm trên đường trung trực của AB(1)
Ta có: HA=HB
nên H nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,I thẳng hàng
Cho đường tròn tâm O bán kính R dây AB không đi qua tâm . Vẽ dây VC vông góc với AB
a, Chứng minh AC là đường kính của đường tròn O
b, Tính R biết AB =12 , BC = 5
Trrinfh bày cách làm nữa nha