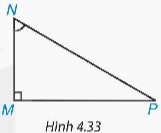
Trong tam giác MNP vuông tại M (H.4.33), \(\sin\widehat{MNP}\) bằng
A. \(\dfrac{PN}{NM}\). B. \(\dfrac{MP}{PN}\). C. \(\dfrac{MN}{PN}\). D. \(\dfrac{MN}{MP}\).
cho tam giác mnp vuông tại p. Hãy giải thích các bàitoans trong trường hợp sau: a)biết cos N=0,5; MN=8cm. tính PN,PM, góc M, góc N. b) biết sin N=0,6; MP=5cm. tính MN,PN, góc M, góc N. c) biết tan N=căn3; MP=6cm. tính MN, PN, góc M, góc N
a: cos N=1/2
=>góc N=60 độ
góc M=90-60=30 độ
Xét ΔMNP vuông tại P có sin M=PN/NM
=>PN/8=sin30=1/2
=>PN=4cm
=>\(PM=\sqrt{8^2-4^2}=4\sqrt{3}\left(cm\right)\)
b: Xét ΔNMP vuông tại P có sin N=0,6=3/5
=>PM/MN=3/5
=>5/MN=3/5
=>MN=25/3
PN=căn (25/3)^2-5^2=20/3(cm)
Xét ΔNMP vuông tại P có sinN=3/5
nên góc N\(\simeq37^0\)
=>\(\widehat{M}\simeq90^0-37^0=53^0\)
c: Xét ΔMNP vuông tại P có tan N=căn 3
=>PM/PN=căn 3
=>6/PN=căn 3
=>PN=2*căn 3(cm)
MN=căn (2*căn 3)^2+6^2=4*căn 3
Xét ΔMNP vuông tại P có tan N=căn 3
nên góc N=60 độ
=>góc M=30 độ
Cho tam giác MNP vuông tại M, đường cao MI(I thuộc NP). Cho PI=6cm, MP= 10 cm. a) Tính PN, MI, góc MNP b) Tính chu vì tam giác MNP c) Gọi H,K lần lượt là hình chiếu của I trên MN, MP. Tính IK
a: ΔPIM vuông tại I
=>IP^2+IM^2=MP^2
=>IM^2=10^2-6^2=64
=>IM=8(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên PI*PN=PM^2
=>PN=10^2/6=50/3(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên MI^2=IN*IP
=>IN=8^2/6=32/3(cm)
Xét ΔMNP vuông tại M có sin MNP=MP/PN
=10:50/3=3/5
=>góc MNP=37 độ
b: C=MN+NP+MP
=10+40/3+50/3
=10+90/3
=10+30
=40(cm)
c: Xét ΔIMP vuông tại I có IK là đường cao
nên IK*PM=IP*IM
=>IK*10=6*8=48
=>IK=4,8(cm)
CHo tam giác MNP vuông tại P, biết
a) PM = 6, MN = 10. Tính PN?
b) PM = 3, MN = 7. Tính PN?
c) Tam giác MNP vuông cân tại P có PM = 2. Tính PN, MN
Hình minh họa :)
a) Xét △MNP vuông tại P
=> PM2 + PN2 = MN2 (định li Pytago)
=> PN2 = MN2 - PM2
=> PN2 = 102 - 62
=> PN2 = 64
=> PN = 8
Vậy PN = 8
b) Xét △MNP vuông tại P
=> PM2 + PN2 = MN2 (định li Pytago)
=> PN2 = MN2 - PM2
=> PN2 = 72 - 32
=> PN2 = 40
=> PN = \(\sqrt{40}\)
Vậy PN = \(\sqrt{40}\)
c) Vì MNP cân tại P => PM = PN => PN = 2
Xét △MNP vuông tại P
=> PM2 + PN2 = MN2 (định li Pytago)
=> MN2 = 2 . 22
=> MN2 = 8
=> MN = \(\sqrt{8}\)
Vậy MN = \(\sqrt{8}\)
CHO tam giácMNP vuông tại M, có góc N=60o và MN =5cm. Tia phân giác của góc N cắt MP tại D kẻ DE vuông PN tại C
A)cm: tam giác MNP = tam giác END
b)CM: tam giác MNE là tam giác đều
c) Tính độ dài cạnh PN
cho tam giác MNP, có MN < MP. Trên tia NM lấy điểm D sao cho ND=NP. Gọi NE là phân giác của góc MNP (E thuộc MP).. Gọi H là giao điểm của NE và PD. Từ M kẻ MI vuông góc PN tại I. Chứng minh rằng:
a)ED=EP
b) BH vuông góc với PD
c) GÓC DNP = 2.^DMI
Cho tam giác MNP vuông tại M, đường cao MI. Biết \(\dfrac{MN}{MP}=\dfrac{3}{4}\); MI=\(\dfrac{48}{5}\) cm.Tính:
a) Độ dài các đoạn thẳng MN, MP, NP.
b) Diện tích tam giác MIP.
\(\dfrac{MN}{MP}=\dfrac{3}{4}\Rightarrow MN=\dfrac{3}{4}MP\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{MI^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{48}{5}\right)^2}=\dfrac{1}{\left(\dfrac{3}{4}MP\right)^2}+\dfrac{1}{MP^2}\)
\(\Rightarrow MP^2=\dfrac{20736}{625}\Rightarrow MP=\dfrac{144}{25}\)
\(\Rightarrow MN=\dfrac{3}{4}MP=\dfrac{108}{25}\)
\(NP=\sqrt{MN^2+MP^2}=\dfrac{36}{5}\)
b. Áp dụng hệ thức lượng:
\(MP^2=IP.NP\Rightarrow IP=\dfrac{MP^2}{NP}=\dfrac{576}{125}\)
\(S_{MIP}=\dfrac{1}{2}IP.MI=\dfrac{13824}{625}\)
1. Cho tam giác MNP cân tại M vẽ MH thuộc NP (H thuộc NP)
a) Chứng minh NH = PH
b) Cho MH = 4 cm; NH = 3 cm. Tính MN
2. Cho tam giác MNP vuông tại M, có góc N = 60o và MN = 5 cm. Tia phân giác của góc N cắt MP tại D. Kẻ DE vuông góc với PN tại E
a) Chứng minh: tam giác MNP = tam giác END
b) Chứng minh: tam giác MNE là tam giác đều
c) Tính độ dài cạnh PN
3. Cho tam giác MNP cân tại M, góc M = 30o; NP = 2 cm. Trên cạnh MP lấy điểm Q sao cho góc PNQ = 60o. Tính độ dài MQ
Cho tam giác ABC=tam giác MNP. Hãy viết kí hiệu bằng nhau của hai tam giác. BIẾT rằng
a)gócA=gócN, gocsB=gócM
b)gocsA=gócB, AC=MN
c)AB=PN, BC=NM
d)AC=PN, AB=MP
e)gócA=gócN, AC=MN
Giúp với mình cần gấp cảm ơn
a, △ABC = △NMP
b, em xem lại em ghi đúng đề chưa
c, △ABC = △PNM
d, △ABC = △PMN
e, △ABC = △NPM
cho ∆ MNP có MP= 6cm; MN= 4,5; PN=7,5.Chứng minh ∆MNP vuông tại M, tính vectơ P,N và đường cao MO của tam giác
Cho tam giác MNP vuông tại M có MP = 6 cm, MN = 8 cm. Kẻ PK là phân giác góc MPN(K thuộc MN). Trên cạnh PN lấy điểm E sao cho PE = PM .
a) Tính độ dài PN b)Chứng minh và
c)Gọi D là giao điểm của tia EK và tia PM. Chứng minh KD = KN
d)Chứng minh tam giác PDN cân
e) Tìm điều kiện của tam giác MNP để tam giác PDN đều
a: PN=10cm
b: Xét ΔPMK vuông tại M và ΔPEK vuông tại E có
PK chung
\(\widehat{MPK}=\widehat{EPK}\)
Do đó: ΔPMK=ΔPEK
c: Xét ΔMKD vuông tại M và ΔEKN vuông tại E có
KM=KE
\(\widehat{MKD}=\widehat{EKN}\)
DO đó: ΔMKD=ΔEKN
Suy ra: KD=KN
d: Ta có: PM+MD=PD
PE+EN=PN
mà PM=PE
và MD=EN
nên PD=PN
hayΔPDN cân tại P