Xét góc C của tam giác ABC vuông tại A (H.4.3). Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Những câu hỏi liên quan
cho tam giác vuông ABC vuông tại A và M là trung điểm của BC, hãy chỉ ra cạnh huyền, cạnh góc vuông, trung tuyến ứng với cạnh huyền. A cho cạnh AB=9cm, AC=12cm. tính BC,MA, diện tích tam giác ABC,ABM? B cho góc B bằng 45 độ, tính góc C, chứng minh tam giác ABC vuông cân và AM vuông góc với bc. tính AM
Hai tam giác vuông ABC (vuông tại đỉnh A) và ABC vuông tại đỉnh A) có tương ứng một cạnh góc vuông và một góc nhọn kề với cạnh ấy bằng nhau: AB AB, widehat B widehat {B} (H.4.46).Dựa vào trường hợp bằng nhau góc cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
Đọc tiếp
Hai tam giác vuông ABC (vuông tại đỉnh A) và ABC vuông tại đỉnh A) có tương ứng một cạnh góc vuông và một góc nhọn kề với cạnh ấy bằng nhau: AB = A'B', \(\widehat B = \widehat {B'}\) (H.4.46).
Dựa vào trường hợp bằng nhau góc cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
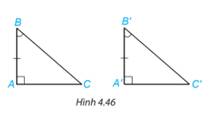
Xét 2 tam giác ABC và A'B'C' có:
\(\widehat B = \widehat {B'}\) (gt)
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(g.c.g)
Đúng 0
Bình luận (0)
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
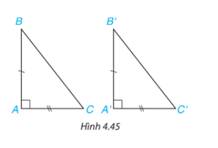
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
Đúng 0
Bình luận (0)
1.Cho tam giác ABC vuông tại A , có góc C =36° , BC = 7cm . Hãy giải tam giác ABC (tìm các cạnh và các góc của tam giác ABC
Ta có:ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=54^0\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin36^0\)
nên \(AB\simeq4,11\left(cm\right)\)
\(\Leftrightarrow AC\simeq5,67\left(cm\right)\)
Đúng 0
Bình luận (0)
15 tháng 3 2022 lúc 8:08
cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AD=AB a) cho AB =6cm AC=8cm Tính độ dài cạnh BC b)chứng minh tam giác ABC= tam giác ADC từ đó suy ra tam giác CBD cân c) từ A kẻ AH vuong góc BC tại H,AK vuông góc Dc tại K Chứng minh HC=KC d)Chứng minh HK song song BD
Cho tam giác ABC vuông tại A, có AB 12cm, BC 20cm1) Tính độ dài cạnh AC và so sánh các góc của tam giác ABC2) Vẽ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho H là trung điểm của đoạn thẳng AD. Chứng minh tam giác AHC tam giác DHC3) Gọi E,F lần lượt là trung điểm của cạnh DC,AC. Đường thẳng DF cắt HC tại M. C/m 3 điểm A,M,E thẳng hàng4) Vẽ tia phân giác của góc BAH cắt cạnh BH tại N. C/m tam giác ANC cân và NH NB
Đọc tiếp
Cho tam giác ABC vuông tại A, có AB = 12cm, BC = 20cm
1) Tính độ dài cạnh AC và so sánh các góc của tam giác ABC
2) Vẽ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho H là trung điểm của đoạn thẳng AD. Chứng minh tam giác AHC = tam giác DHC
3) Gọi E,F lần lượt là trung điểm của cạnh DC,AC. Đường thẳng DF cắt HC tại M. C/m 3 điểm A,M,E thẳng hàng
4) Vẽ tia phân giác của góc BAH cắt cạnh BH tại N. C/m tam giác ANC cân và NH < NB
cho tam giác ABC vuông tại A có GÓC B=60 độ .Vẽ AH vuông góc với AH tại H .
a, Tính số đo góc HAB
b, Trên cạnh AC lấy D sao cho AD=AH .Gọi I là trung điểm của cạnh HD.Chứng minh tam giác AHI=tam giác ADI .Từ đó suy ra AI vuông góc với HD.
c,Tia AI cắt cạnh Hc tại K. Chứng minh AB//KD.
a: \(\widehat{HAB}=30^0\)
b: Xét ΔAHI và ΔADI có
AH=AD
AI chung
HI=DI
Do đó: ΔAHI=ΔADI
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có góc ACB=65 độ.Kẻ AH vuông góc BC tại H,trên tia đối của tia HA lấy điểm E sao cho HE=HA.Gọi M là trung điểm cạnh BC,trên tia đối của MA lấy điểm D sao cho MD=MA.
a,Tính số đo góc ABC và so sánh AB và AC.
b,Chứng minh tam giác ABH bằng tam giác EBH,từ đó suy ra tam giác ABE cân tại B
c, Chứng minh tam giác BEC vuông tại E
d,Chứng minh ED song song với BC
a, áp dụng tổng 3 góc trong 1 tam giác => góc AB= 25 độ
AC < AB ( 65 độ > 25 độ)
b, Xét tam giác BHC và tam giác BHE có: BH- chung ; BHA = BHE (=90 độ) ; AH = HE ( theo đề bài)
=> hai tam giác bằng nhau (c.g.c) => BA = BE => tam giác BEA cân tại B (đpcm)
c, Dễ dàng chứng minh được tam giác BEC = tam giác BAC
=> BEC = BAC = 90 độ
=> tam giác BEC vuông tại E (đpcm)
d, Ta có: MH đi qua trung điểm của AD và AE trong tam giác ADE => NM là đường trung bình của tam giác này => MN // DE (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ am vuông BC tại M.a) C/m tam giác ABMACM và M là trung điểm của cạnh BCb) Qua C kẻ đường thẳng vuông góc với AC cắt đường thẳng AM tại E .C/m tam giác ABEACE và BE vuông góc với ABc) Trên tia đối của tia CA lấy điểm D sao cho ACDC. Qua D kẻ đường thẳng vuông góc với BC cắt đường thẳng CE tại F . C/m C là trung điểm của cạnh FEd) Cho AC 10cm , BC 12cm,ME4,5cm. Tính độ dài đoạn thẳng DF
Đọc tiếp
Cho tam giác ABC cân tại A. Kẻ am vuông BC tại M.
a) C/m tam giác ABM=ACM và M là trung điểm của cạnh BC
b) Qua C kẻ đường thẳng vuông góc với AC cắt đường thẳng AM tại E .C/m tam giác ABE=ACE và BE vuông góc với AB
c) Trên tia đối của tia CA lấy điểm D sao cho AC=DC. Qua D kẻ đường thẳng vuông góc với BC cắt đường thẳng CE tại F . C/m C là trung điểm của cạnh FE
d) Cho AC = 10cm , BC = 12cm,ME=4,5cm. Tính độ dài đoạn thẳng DF
Cho Tam giác ABC vuông tại A, có góc ABC 60 độ, tia phân giác góc ABC cắt AC tại D.Từ D kẻ DH vuông góc với BC tại H, gọi giao điểm của DH và AB là K.a/ Chứng minh AD DHb/ So sánh độ dài cạnh AD và DCc/ Chứng minh tam giác KBC là tam giác đềud/ Chứng minh KD là đường trung trực của BC từ đó suy ra B đối xứng với C qua KD( Giusp với Hãy giúp tôi với )))* Cầu xin *
Đọc tiếp
Cho Tam giác ABC vuông tại A, có góc ABC = 60 độ, tia phân giác góc ABC cắt AC tại D.Từ D kẻ DH vuông góc với BC tại H, gọi giao điểm của DH và AB là K.
a/ Chứng minh AD= DH
b/ So sánh độ dài cạnh AD và DC
c/ Chứng minh tam giác KBC là tam giác đều
d/ Chứng minh KD là đường trung trực của BC từ đó suy ra B đối xứng với C qua KD
( Giusp với Hãy giúp tôi với =)))
* Cầu xin *
