Lập bảng tần số tương đối của mẫu số liệu thống kê trong Hoạt động 1.

Những câu hỏi liên quan
Thống kê số huy chương bốn quốc gia dẫn đầu SEA Games 31 được cho trong bảng số liệu sau:Hãy chuyển dữ liệu đã cho vào bảng thống kê theo mẫu dưới đây và vào biểu đồ cột kép tương ứng.
Đọc tiếp
Thống kê số huy chương bốn quốc gia dẫn đầu SEA Games 31 được cho trong bảng số liệu sau:
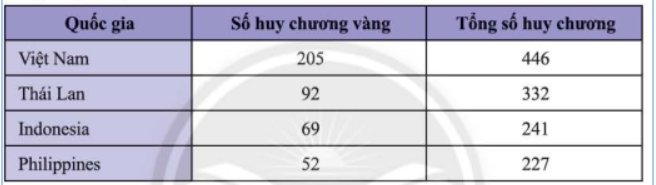
Hãy chuyển dữ liệu đã cho vào bảng thống kê theo mẫu dưới đây và vào biểu đồ cột kép tương ứng.

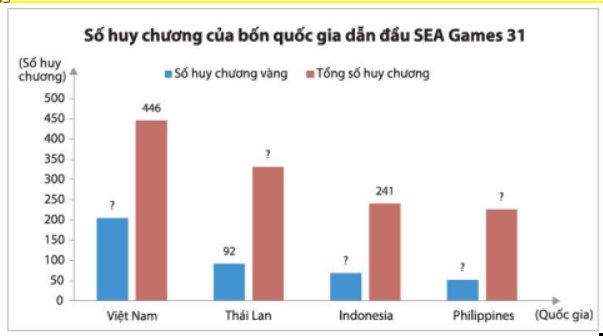
Điền số vào bảng: 446 92 69 227
Biểu đồ; 205 322 69 52 227
Đúng 0
Bình luận (0)
Thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau: Lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau: [1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10] Từ đó; chọn mệnh đề đúng trong các mệnh đề sau? A. Lớp 2 và 4 có cùng tần số B. Lớp 5 có tần suất cao nhất C. Lớp 3 có tần số thấp nhất D. tất cả sai
Đọc tiếp
Thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau:
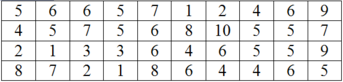
Lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau:
[1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10]
Từ đó; chọn mệnh đề đúng trong các mệnh đề sau?
A. Lớp 2 và 4 có cùng tần số
B. Lớp 5 có tần suất cao nhất
C. Lớp 3 có tần số thấp nhất
D. tất cả sai
Chọn A.
Bảng phân bố tần số - tần suất
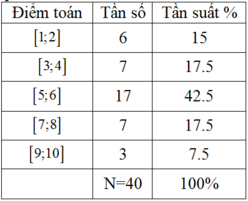
Dựa vào bảng trên ta thấy lớp 3 có tần số và tần suất cao nhất; lớp 5 có tần số; tần suất thấp nhất.
Lớp 2 và 4 có cùng tần số và tần suất.
Đúng 0
Bình luận (0)
Hãy lập bảng dữ liệu ban đầu để điều tra số thành viên trong gia đình của các bạn trong tổ em và lập bảng thống kê tương ứng.
Em khảo sát dữ liệu của các bạn trong lớp rồi điền vào bảng.
Ví dụ:
Đúng 0
Bình luận (0)
Xét bảng 2 (được lập ở bài tập mẫu của bài 1) Để mô tả bảng 2 và trình bày các số liệu thống kê, người ta vẽ biểu đồ tần số hình cột dưới đây (h.55)Hình 55. Biểu đồ tần số hình cột về thành tích chạy 50m của học sinh lớp 10A trường Trung học phổ thông C (đơn vị là giây) Dựa vào biểu đồ trên, có thể vẽ được đường gấp khúc tần số (kí hiệu là D), cũng để mô tả bảng 2 và trình bày các số liệu thống kê. Đường gấp khúc tần số D như vậy là đường gấp khúc nào dưới đây (h.55)?
Đọc tiếp
Xét bảng 2 (được lập ở bài tập mẫu của bài 1)
Để mô tả bảng 2 và trình bày các số liệu thống kê, người ta vẽ biểu đồ tần số hình cột dưới đây (h.55)
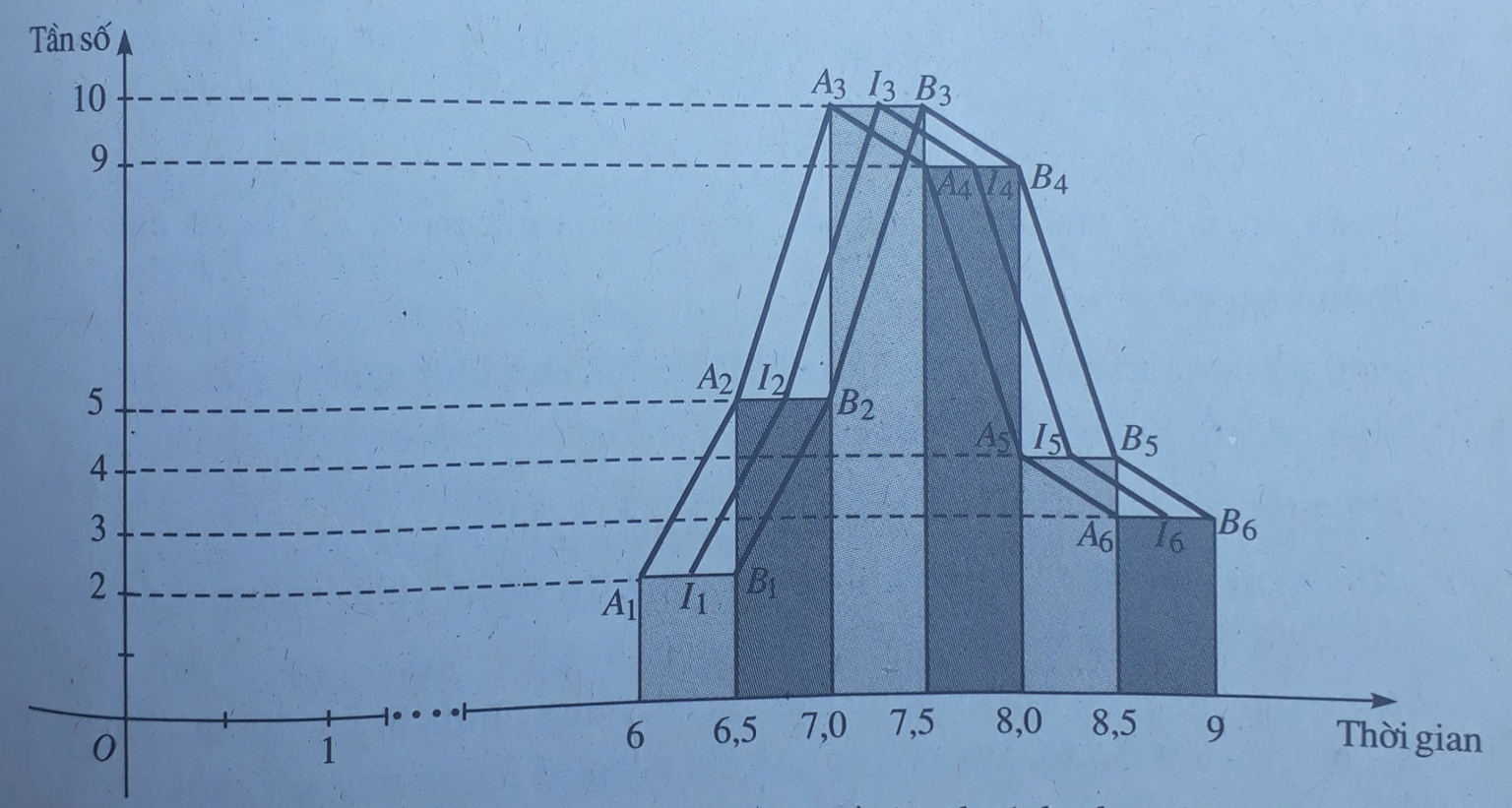
Hình 55. Biểu đồ tần số hình cột về thành tích chạy 50m của học sinh lớp 10A trường Trung học phổ thông C (đơn vị là giây)
Dựa vào biểu đồ trên, có thể vẽ được đường gấp khúc tần số (kí hiệu là D), cũng để mô tả bảng 2 và trình bày các số liệu thống kê.
Đường gấp khúc tần số D như vậy là đường gấp khúc nào dưới đây (h.55)?
Các đỉnh của đường gấp khúc tần số có tọa độ là ( c i ; n i ), với c i là giá trị đại diện của lớp thứ i, n i là tần số của lớp thứ i. Từ đó suy ra: các đỉnh của đường gấp khúc tần số là các trung điểm của các cạnh phía trên của các cột (các hình chữ nhật) của biểu đồ tần số hình cột
Đường gấp khúc I 1 I 2 I 3 I 4 I 5 I 6 với I 1 , I 2 , I 3 , I 4 , I 5 , I 6 lần lượt là trung điểm của các đoạn thẳng A 1 B 1 , A 2 B 2 , A 3 B 3 , A 4 B 4 , A 5 B 5 , A 6 B 6
Đúng 0
Bình luận (0)
Thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau: Lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau: [1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10] Hỏi có mấy lớp có tần suất không bé hơn 17,5% A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau:
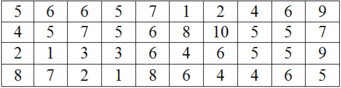
Lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau:
[1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10]
Hỏi có mấy lớp có tần suất không bé hơn 17,5%
A. 1
B. 2
C. 3
D. 4
Chọn C.
Bảng phân bố tần số - tần suất
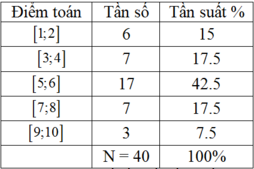
Dựa vào bảng phân bố tần số; tần suất trên ta thấy có 3 lớp có tần suất không bé hơn 17,5% là lớp thứ 2;3 và lớp thứ 4.
Đúng 0
Bình luận (0)
Bảng sau thống kê số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam. (Nguồn: worldometers.info)a) Xác định số trung bình và tứ phân vị của mẫu số liệu trên. Mẫu số liệu có bao nhiêu giá trị ngoại lệ?b) Hoàn thiện bảng tần số ghép nhóm theo mẫu sau: c) Hãy ước lượng số trung bình và tứ phân vị của mẫu số liệu ở bảng tần số ghép nhóm trên.
Đọc tiếp
Bảng sau thống kê số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam.

(Nguồn: worldometers.info)
a) Xác định số trung bình và tứ phân vị của mẫu số liệu trên. Mẫu số liệu có bao nhiêu giá trị ngoại lệ?
b) Hoàn thiện bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng số trung bình và tứ phân vị của mẫu số liệu ở bảng tần số ghép nhóm trên.
Tham khảo:
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:
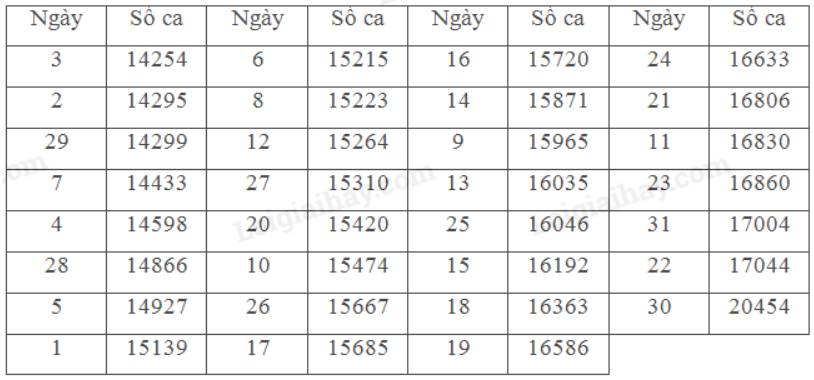
Số trung bình của số liệu là: \(\bar x \approx 15821,87\)
Tứ phân vị thứ nhất là: \({x_8} = 15139\)
Tứ phân vị thứ hai là: \({x_{16}} = 15685\)
Tứ phân vị thứ ba là: \({x_{24}} = 16586\)
Mẫu số liệu có 1 giá trị ngoại lệ.
b)

c) Ta có:

• Số ca nhiễm mới SARS-CoV-2 trung bình trong tháng 12/2021 tại Việt Nam là:
\(\bar x = \frac{{14.14,74 + 14.16,25 + 2.17,75 + 0.19,25 + 1.20,75}}{{31}} \approx 15,81\)
• Gọi \({x_1};{x_2};...;{x_{31}}\) số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{14}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}}\end{array}}\end{array};{x_{15}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{c}}{\left[ {17;18,5} \right)}\end{array};{x_{31}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {20;21,5} \right)}\end{array}}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \({x_{16}}\)
Ta có: \(n = 31;{n_m} = 14;C = 14;{u_m} = 15,5;{u_{m + 1}} = 17\)
Do \({x_{16}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 15,5 + \frac{{\frac{{31}}{2} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 15,66\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 31;{n_m} = 14;C = 0;{u_m} = 14;{u_{m + 1}} = 15,5\)
Do \({x_8} \in \begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 14 + \frac{{\frac{{31}}{4} - 0}}{{14}}.\left( {15,5 - 14} \right) \approx 14,83\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{24}}\).
Ta có: \(n = 31;{n_j} = 14;C = 14;{u_j} = 15,5;{u_{j + 1}} = 17\)
Do \({x_{24}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 15,5 + \frac{{\frac{{3.31}}{4} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 16,49\)
Đúng 0
Bình luận (0)
Biểu đồ ở Hình 7 biểu diễn lượng mưa tại trạm khí tượng Huế trong sáu tháng cuối năm dương lịch.a) Nêu đối tượng thống kê và tiêu chí thống kê.b) Lập bảng số liệu thống kê lượng mưa tại trạm khí tượng Huế theo mẫu sau:c) Trong các tháng trên, tháng nào có lượng mưa nhiều nhất? Tháng nào có lượng mưa ít nhất?
Đọc tiếp
Biểu đồ ở Hình 7 biểu diễn lượng mưa tại trạm khí tượng Huế trong sáu tháng cuối năm dương lịch.
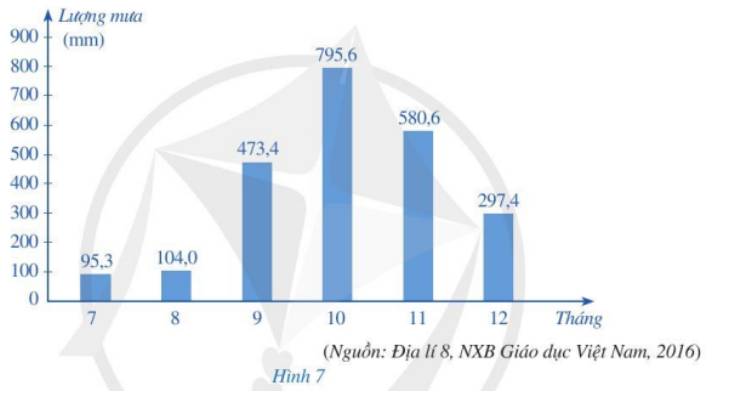
a) Nêu đối tượng thống kê và tiêu chí thống kê.
b) Lập bảng số liệu thống kê lượng mưa tại trạm khí tượng Huế theo mẫu sau:

c) Trong các tháng trên, tháng nào có lượng mưa nhiều nhất? Tháng nào có lượng mưa ít nhất?
a)
- Đối tượng thống kê là lượng mưa tại trạm khí tượng Huế.
- Tiêu chí thống kê là lượng mưa tại trạm khí tượng Huế trong sáu tháng cuối năm dương lịch.
b) Bảng số liệu thống kê lượng mưa tại trạm khí tượng Huế:
Tháng | 7 | 8 | 9 | 10 | 11 | 12 |
Lượng mưa (mm) | 95,3 | 104,0 | 473,4 | 795,6 | 580,6 | 297,4 |
c) Ta thấy:
95,3 < 104,0 < 297,4 < 473,4 < 580,6 < 795,6 (mm)
Vậy lượng mưa tại trạm khí tượng Huế vào: tháng 7 < tháng 8 < tháng 12 < tháng 9 < tháng 11 < tháng 10
Hay trong các tháng trên, tháng 10 có lượng mưa lớn nhất, tháng 7 có lượng mưa ít nhất.
Đúng 0
Bình luận (0)
Cho các số liệu thống kê ghi trong bảng sau:
Thời gian (phút) đi từ nhà đến trường của A trong 35 ngày

Lập bảng phân bổ tần số và tần suất ghép lớp, với các lớp
[19;21); [21;23); [23;25); [25;27); [27; 29].
Thời gian đi từ nhà đến trường của bạn A trong 35 ngày
| Lớp thời gian (phút) | Tần số | Tần suất (%) |
| [19;21) | 5 | 14,29 |
| [21;23) | 9 | 25,71 |
| [23;25) | 10 | 28,57 |
| [25;27) | 7 | 20,00 |
| [27; 29] | 4 | 11,43 |
| Cộng | 35 | 100& |
Đúng 0
Bình luận (0)
Cho các số liệu thống kê ghi trong bảng sau:
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân (đơn vị: phút)

Hãy lập bảng phân bố tần số, bảng phân bố tần suất
Bảng phân bố tần số
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 50 | 54 | cộng |
| Tần số | 4 | 5 | 20 | 10 | 8 | 3 | 50 |
Bảng phân bố tần suất
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 20 | 54 | Cộng |
| Tần suất (%) | 8 | 10 | 40 | 20 | 16 | 6 | 100% |
Đúng 0
Bình luận (0)
Một cửa hàng đã thống kê số ba lỗ bán được mỗi ngày trong tháng 9 với kết quả cho như sau:

Hãy chia mẫu số liệu trên thành 5 nhóm, lập tần số ghép nhóm, hiệu chỉnh bảng và xác định giá trị đại diện cho mỗi nhóm.
Tham khảo:
Khoảng biến thiên của mẫu số liệu trên là \(R = 29 - 10 = 19\).
Độ dài mỗi nhóm \(L > \frac{R}{k} = \frac{{19}}{5} = 3,8\).
Ta chọn \(L = 4\) và chia dữ liệu thành các nhóm: \(\left[ {10;14} \right),\left[ {14;18} \right),\left[ {18;22} \right),\left[ {22;26} \right),\left[ {26;30} \right)\).
Khi đó ta có bảng tần số ghép nhóm sau:

Đúng 0
Bình luận (0)











