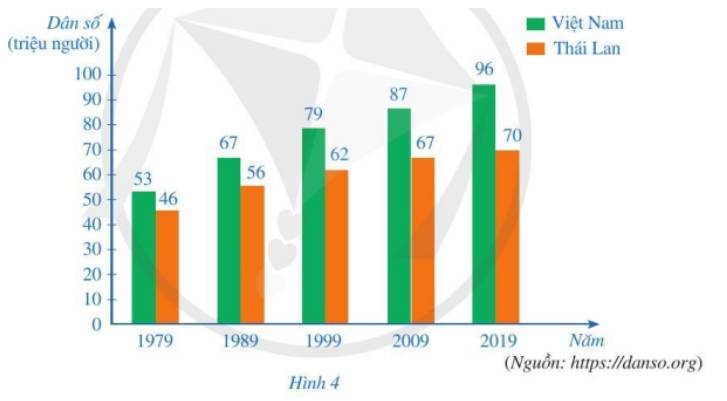
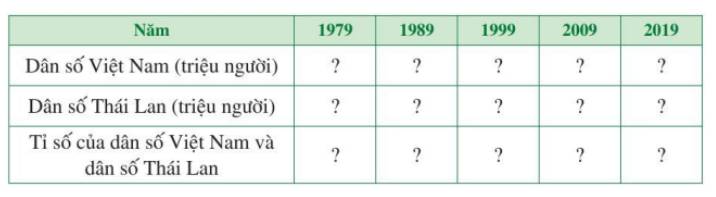
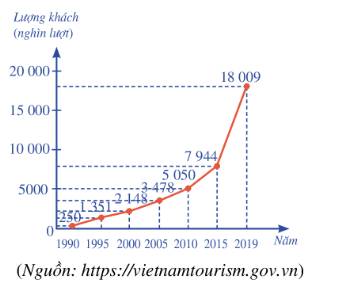
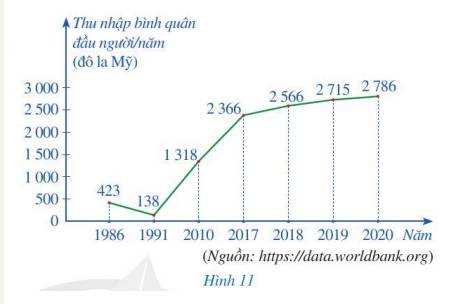
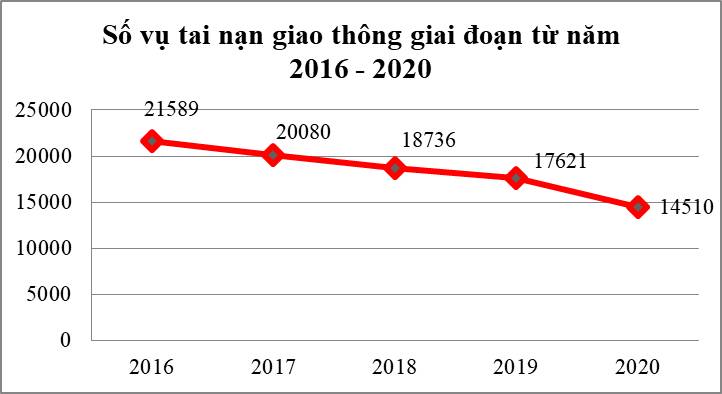
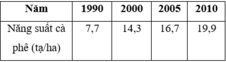
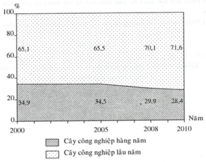
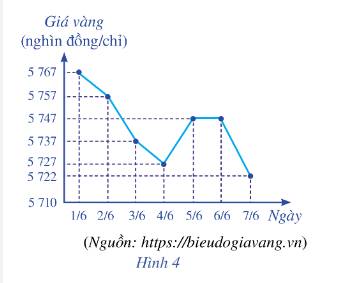
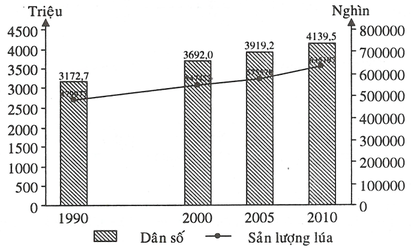
Biểu đồ cột ở Hình 14 biểu diễn số người tham gia bảo hiểm y tế (BHYT) của Việt Nam ở một số năm trong giai đoạn từ năm 2010 đến năm 2019.
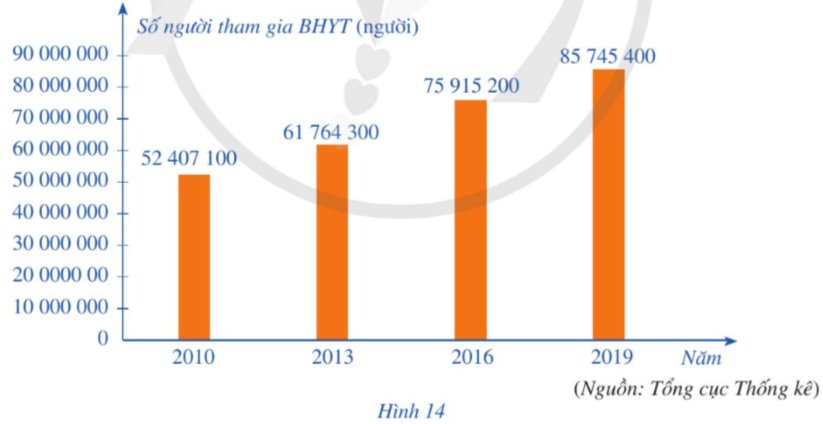
a) Vẽ biểu đồ đoạn thẳng biểu diễn những dữ liệu thống kê trong biểu đồ cột ở Hình 14.
b) Một người đưa ra nhận định: Từ năm 2010 đến năm 2019, số người tham gia bảo hiểm y tế của nước ta đã tăng lên 65%. Hỏi nhận định của người đó là đúng hay sai?