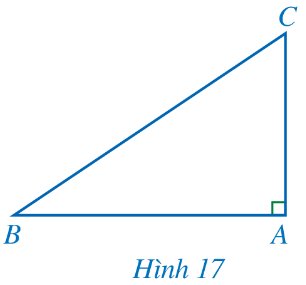
Tính độ dài cạnh AB trong Hình 17 khi AC = 4 cm và \(\widehat{B}\) = 34° (làm tròn kết quả đến hàng phần mười của centimét).
Cho tam giác ABC có \(AB = 3,5;\;AC = 7,5;\;\widehat A = {135^o}.\) Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)
Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)
Dùng máy tính cầm tay để A) tính độ dài cạnh của một miếng đất hình vuông có S=12 996m² B) Tính bán kính của 1 hình tròn có S=100 cm²(làm tròn kết quả đến hàng phần mười)
Lời giải:
a. Ta có: $12996=114\times 114$ nên độ dài cạnh miếng đất là $114$ (m)
b. $3,14 R^2=100$
$R^2=100:3,14$=31,84$
$R=\sqrt{31,84}=5,6$ (cm)
Cho tam giác ABC có \(AB = 3,AC = 4,\widehat {BAC} = {120^o}.\) Tính (làm tròn kết quả đến hàng đơn vị):
a) Độ dài cạnh BC và độ lớn góc B.
b) Bán kính đường tròn ngoại tiếp
c) Diện tích của tam giác
d) Độ dài đường cao xuất phát từ A
e) \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {BC} \) với M là trung điểm của BC.
a) Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {3^2} + {4^2} - 2.3.4.\cos {120^o}\\ \Leftrightarrow B{C^2} = 37\\ \Leftrightarrow BC \approx 6\end{array}\)
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = 2R\\ \Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{4.\sin {{120}^o}}}{6} = \frac{{\sqrt 3 }}{3}\\ \Leftrightarrow \widehat B \approx {35^o}\end{array}\)
b) \(R = \frac{{BC}}{{2.\sin A}} = \frac{6}{{2.\sin {{120}^o}}} = 2\sqrt 3 \)
c) Diện tích tam giác ABC: \(S = \frac{1}{2}4.3.\sin {120^o} = 3\sqrt 3 .\)
d) Gọi H là chân đường cao hạ từ đỉnh A.
Ta có: \(S = \frac{1}{2}AH.BC\)
\( \Rightarrow AH = \frac{{2S}}{{BC}} = \frac{{2.3\sqrt 3 }}{6} = \sqrt 3 \)
e) \(\overrightarrow {AB} .\overrightarrow {AC} = 3.4.\cos (\widehat {BAC}) = 12.\cos {120^o} = - 6.\)
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \) (do M là trung điểm BC)
\( \Leftrightarrow \overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )\)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} .\overrightarrow {BC} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )(\overrightarrow {AC} - \overrightarrow {AB} )\\ = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} - {{\overrightarrow {AB} }^2}} \right) = \frac{1}{2}\left( {A{C^2} - A{B^2}} \right)\\ = \frac{1}{2}\left( {{4^2} - {3^2}} \right) = \frac{7}{2}.\end{array}\)
Cho hình 16.
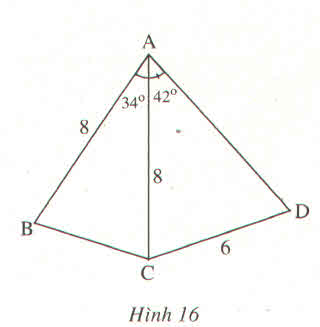
Biết \(AB=AC=8cm,CD=6cm,\widehat{BAC}=34^0,\widehat{CAD}=42^0\). Hãy tính :
a) Độ dài cạnh BC
b) \(\widehat{ADC}\)
c) Khoảng cách từ điểm B đến cạnh AD
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là:92,1
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:-845,7
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là:-72,9
\(92,117\approx92,12\\ -845,654\approx-845,65\approx-845,7\\ 82,572\approx82,57\\ 82,572\approx82,57\\ -72,882\approx-72,9\)
Cho tam giác ABC vuông ở A, đường cao AH, biết BH = 4 cm, CH = 9 cm. Hãy tính ( kết quả về độ dài là tròn đến chữ số thập phân thứ ba, số đo góc làm tròn đến độ):
a. Dộ dài cạnh AB và đường cao AH.
b. Góc B rồi từ đó tính độ dài cạnh AC.
c. Diện tích tam giác ABC.
Cho biết 1 inch = 2,54 cm. Tính độ dài đường chéo bằng đơn vị cm một màn hình 48 inch và làm tròn đến hàng phần mười.
Độ dài đường chéo của màn hình 48 inch là: \(48.2,54 = 121,92 \approx 121,9\) (cm).
Câu 9: Chia đều 1 thanh gỗ dài 8,32m thành 4 đoạn thẳng bằng nhau. Tính độ dài mỗi đoạn gỗ ( Làm tròn kết quả đến hàng phần mười)
A.2m B.2,18m C.2,1m D.2,08m
Cho hình 14 :
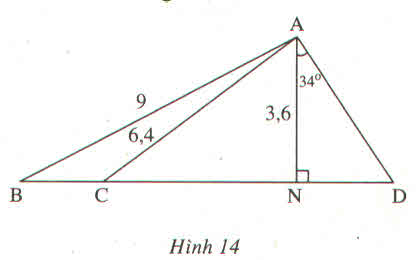
Biết \(AB=9cm,AC=6,4cm,AN=3,6cm,\widehat{AND}=90^0,\widehat{DAN}=34^0\). Hãy tính :
a) CN
b) \(\widehat{ABN}\)
c) \(\widehat{CAN}\)
d) AD
(Các kết quả tính góc được làm tròn đến phút và các kết quả tính độ dài và tính các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ tư)
Bài 3: Để chạy xe từ sân lên nhà, người ta làm một cầu dắt xe như hình vẽ. Biết độ cao của bậc thềm AB = 55 cm, chiều dài từ chân bậc thềm tới điểm đặt còn lại của cầu dắt xe là AC = 75cm. Tính chiều dài của cầu dắt xe (kết quả làm tròn đến hàng phần mười)? (1đ)
Bài 4: Hình bên là một cái lều ở một trại hè của học sinh tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ:
a/ Thể tích không khí bên trong lều là bao nhiêu biết chiều cao của chiếc lều là 2,8 m và độ dài cạnh đáy của lều 4,8 m ?
b/ Xác định số vải bạt cần thiết để dựng lều ( không tính đến đường viền, nếp gấp, đáy…) là bao nhiêu ? Biết chiều cao mặt bên của lều trại là 4m
Bài : Cho tam giác ABC vuông tại A ( AB < AC). Gọi M là trung điểm BC. Gọi D, E lần lượt là hình chiếu của M lên AB và AC.
a/ Chứng minh: ADME là hình chữ nhật (1 đ)
b/ Chứng minh: D là trung điểm của AB và BMEB là hình bình hành. (1 đ)
c/ Gọi N là điểm đối xứng của M qua D, P là điểm đối xứng của M qua E. Chứng minh: P, A, N thẳng hàng (0,5 đ)
E cảm ơn nhiều ạa
Bài 3,4: Bạn cho mình xin hình vẽ nha bạn
Bài 5:
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b:
Sửa đề: Chứng minh BMED là hình bình hành
Xét ΔABC có
M là trung điểm của BC
MD//AC(Cùng vuông góc với AB)
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB(cùng vuông góc với AC)
Do đó: E là trung điểm của AC
Xét ΔABC có
E,M lần lượt là trung điểm của CA,CB
=>EM là đường trung bình của ΔABC
=>EM//AB và \(EM=\dfrac{AB}{2}\)
Ta có: EM//AB
D\(\in\)AB
Do đó: EM//BD
Ta có: \(EM=\dfrac{AB}{2}\)
\(DB=\dfrac{AB}{2}\)
Do đó: EM=BD
Xét tứ giác EMBD có
EM//BD
EM=BD
Do đó: EMBD là hình bình hành
c: Xét tứ giác AMBN có
D là trung điểm chung của AB và MN
=>AMBN là hình bình hành
Hình bình hành AMBN có MN\(\perp\)AB
nên AMBN là hình bình hành
=>AB là phân giác của góc MAN
=>\(\widehat{MAN}=2\cdot\widehat{MAB}\)
Xét tứ giác AMCP có
E là trung điểm chung của AC và MP
=>AMCP là hình bình hành
Hình bình hành AMCP có AC\(\perp\)MP
nên AMCP là hình thoi
=>AC là phân giác của góc MAP
=>\(\widehat{MAP}=2\cdot\widehat{MAC}\)
Ta có: \(\widehat{MAP}+\widehat{MAN}=\widehat{PAN}\)
=>\(\widehat{PAN}=2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)\)
=>\(\widehat{PAN}=2\cdot\widehat{BAC}=180^0\)
=>P,A,N thẳng hàng