Hình 12 mô tả đường lên dốc ở Hình 11, trong đó góc giữa BC và phương nằm giữa BA là \(\widehat{ABC}=15^o\).

Cạnh góc vuông AC và cạnh huyền BC (Hình 12) có liên hệ với nhau như thế nào?
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và(ABC).
A. 30°
B. 45°
C. 60°
D. 75°
Đáp án C
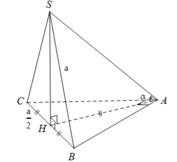
- Gọi H là trung điểm của BC suy ra:
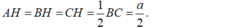
- Ta có:
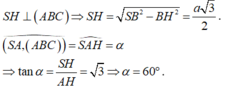
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên mp(ABC) trùng với trung điểm BC, biết SB = a. Tính số đo của góc giữa SA và mp(ABC).
A. 30°
B. 45°
C. 60°
D. 75°
Chọn C.
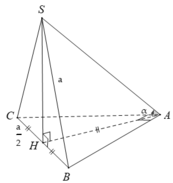
- Gọi H là trung điểm của BC. Suy ra:
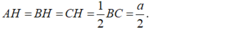
- Ta có:
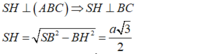
- Do H là hình chiếu của S lên mp(ABC) nên góc giữa đường thẳng SA và mp (ABC) là góc 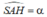
- Xét tam giác vuông SHA có:
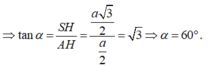
Cho một tam giác ABC vuông tại A có \(\widehat{B}=\dfrac{1}{2}\widehat{C}\). Kẻ đường cao AH sao cho cạnh AH vuông góc với cạnh huyền BC tại H. Các hình chiếu của AB và AC trên BC lần lượt là BH và HC. Biết HC = 1,6cm.
a) Tính góc B và C, và các tỉ số lượng giác của chúng nó.
b*) Tính độ dài các cạnh BC, AB và AC.
Gợi ý: Sử dụng các hệ thức về tỉ số lượng giác của góc nhọn và một trong bốn hệ thức về cạnh góc vuông và đường cao trong tam giác vuông để tính.
c) Tính độ dài các cạnh AH và BH.
d) Hãy chứng minh rằng: Cả ba tam giác vuông ABC, HBA và HAC đồng dạng với nhau.
e*) Chứng minh rằng: \(\dfrac{\sin\widehat{HAC}}{\cos\widehat{HBA}}\div\dfrac{\tan\widehat{HAC}}{\cot\widehat{ABC}}=\dfrac{csc^2\widehat{ABC}}{sec^2\widehat{ABC}\cdot\cot\widehat{HBA}}\)
Gợi ý:
1. Secant - sec α nghịch đảo với cos α
2. Cosecant - csc α nghịch đảo với sin α
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD); M, N là hai điểm nằm trên hai cạnh BC, CD. Đặt B M = x , D N = y 0 < x , y < a . Hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SMN) vuông góc với nhau là:
A. x 2 + a 2 = a x + 2 y .
B. x 2 + a 2 = a x + y .
C. x 2 + 2 a 2 = a x + y .
D. 2 x 2 + a 2 = a x + y .
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD); M, N là hai điểm nằm trên hai cạnh BC, CD. Đặt BM=x, DN=y (0<x,y<a). Hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SMN) vuông góc với nhau là:
![]()
![]()
![]()
![]()
Cho ∆ABC vuông tại A, đường cao AH. Biết tỉ số AB/AC=5/12, cạnh huyền BC = 26cm. Tính độ dài 2 cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
AB/AC=5/12
=>AB/5=AC/12=k
=>AB=5k; AC=12k
ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>25k^2+144k^2=26^2
=>169k^2=26^2
=>k^2=4
=>k=2
=>AB=10cm; AC=24cm
ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2; CH*CB=CA^2
=>BH=10^2/26=100/26=50/13(cm); CH=24^2/26=288/13(cm)
Cho tam giác vuông ABC có AB=3/4; AC-AB=3cm. Biết đường vuông góc kẻ từ A đến cạnh huyền BC là 7,2cm. Tính độ dài hai hình chiếu của 2 cạnh góc vuông AB và AC lên BC.
Hình chóp tam giác S.ABC có đáy là tam giác đều ABC cạnh 7a, có cạnh SC vuông góc với mặt phẳng đáy (ABC) và SC = 7a.
a) Tính góc giữa SA và BC.
b) Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC.
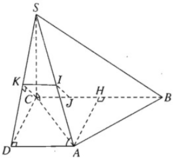
a) Gọi H là trung điểm của đoạn BC. Qua A vẽ AD song song với BC và bằng đoạn HC thì góc giữa BC và SA là góc ∠SAD. Theo định lí ba đường vuông góc, ta có SD ⊥ DA và khi đó:
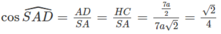
Vậy góc giữa BC và SA được xác định sao cho 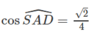
Vì BC // AD nên BC song song với mặt phẳng (SAD). Do đó khoảng cách giữa SA và BC chính là khoảng cách từ đường thẳng BC đến mặt phẳng (SAD).
Ta kẻ CK ⊥ SD, suy ra CK ⊥ (SAD), do đó CK chính là khoảng cách nói trên. Xét tam giác vuông SCD với đường cao CK xuất phát từ đỉnh góc vuông C ta có hệ thức:

Chú ý. Nếu kẻ KI // AD và kẻ IJ // CK thì IJ là đoạn vuông góc chung của SA và BC.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC.
A. a 3 2
B. a
C. a 3 4
D. a 2
Cho hình thang cân ABCD có AD//BC , AD<BC , AB vuông góc với AC , AB =3 cm , AC =4cm
A) viết hệ thức liên hệ giữa 3 cạnh của tam giác ABC
B) tính độ dài BC
C) tính độ đai BD và DC
a: AB\(\perp\)AC
=>ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
b: Ta có: \(BC^2=AB^2+AC^2\)
=>\(BC^2=3^2+4^2=25\)
=>\(BC=\sqrt{25}=5\left(cm\right)\)
c: ABCD là hình thang cân
=>BD=AC
mà AC=4cm
nên BD=4cm