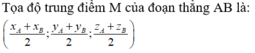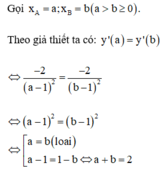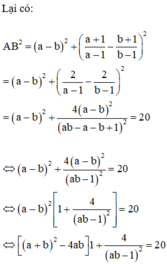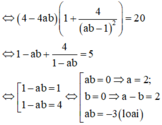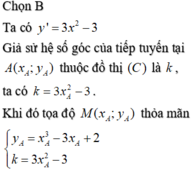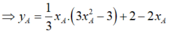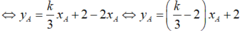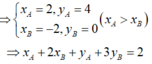Cho hai điểm A(xA; yA; zA), B(xB; yB; zB). Từ biểu thức \(\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\), tìm tọa độ của vectơ \(\overrightarrow{AB}\) theo tọa độ hai điểm A, B.

Những câu hỏi liên quan
tìm m để (d) cắt (P) tại 2 điểm phân biệt A,B sao cho |xA-xB| nhỏ hơn 3
biết xA và xB lần lượt là hoành độ giao điểm của hai điểm A,B
chỉ mình cách làm nha
cho hàm số y=2x^2 có đồ thị (P)
a) Trên (P) lấy hai điểm A và B thỏa mãn xA=1,xB=-2 viết pt đường thẳng đi qua hai điểm A và B
Vì A,B thuộc (P) nên \(\left\{{}\begin{matrix}y_A=2x_A^2=2\\y_B=2x_B^2=8\end{matrix}\right.\)
\(\Rightarrow A\left(1;2\right)\\ B\left(-2;8\right)\)
Đúng 1
Bình luận (0)
Gọi (d): y=ax+b
Vì (d) đi qua hai điểm A(1;2) và B(-2;8) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=1\\-2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-7\\a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{7}{3}\\b=1-a=1+\dfrac{7}{3}=\dfrac{10}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai điểm A, B có tọa độ các điểm A(
x
A
;
y
A
;
z
A
), B(
x
B
;
y
B
;
z
B
). Tọa độ trung điểm M của đoạn thẳng AB là: A.
x...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A, B có tọa độ các điểm A( x A ; y A ; z A ), B( x B ; y B ; z B ). Tọa độ trung điểm M của đoạn thẳng AB là:
A. x A + x B ; y A + y B ; z A + z B
B. x B - x A ; y B - y A ; z B - z A
C. x A + x B 2 ; y A + y B 2 ; z A + z B 2
D. x B - x A 2 ; y B - y A 2 ; z B - z A 2
Cho hàm số
y
x
+
1
x
-
1
có đồ thị (C). Gọi A B
x
A
x
B
≥
0
là hai điểm trên (C) có tiếp tuyến tại A,B song song nhau và
A
B...
Đọc tiếp
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi A < B x A > x B ≥ 0 là hai điểm trên (C) có tiếp tuyến tại A,B song song nhau và A B = 2 5 . Hiệu x A - x B bằng?
A. 2
B. 4
C. 2 2
D. 2
2/ Cho parabol (P): y=x2
và đường thẳng (d) có hệ số góc là a khác 0 đi qua điểm M(1;2)
a/ Cm rằng (d) luôn luôn cắt P tại hai điểm phân biệt với mọi a khác 0.
b/ Gọi xA và xB là hoành độ giao điểm của P và d. Chứng minh rằng xA+xB-xA.xB=2.
Bài này sử dựng định lý viet để chứng minh:
Gọi phương trình đường thẳng (d) có hệ số góc a có dạng : \(y=ax+b\left(a\ne0\right)\); \(M\left(1,2\right)\)thuộc (d) nên : \(2=a+b\Rightarrow b=2-a\left(1\right)\). Xét phương trình hoành độ giao điểm có : \(x^2=ax+b\left(2\right)\)thế 1 vào 2 có \(x^2=ax+2-a\Leftrightarrow x^2-ax-\left(2-a\right)=0\)phương trình có : \(\Delta=a^2+4\left(2-a\right)=a^2-4a+8\)\(\Rightarrow\Delta=\left(a^2-4a+4\right)+4=\left(a-2\right)^2+4\ge4\forall a\) nên phương trình luôn có hai nghiệm phân biệt với mọi giá tri của \(a\ne0\)Khi đó parabol cắt d tại hai điểm A,B với A,B có hoành độ lần lượt là \(x_A,x_B\) theo vi ét ta có : \(\hept{\begin{cases}x_A+x_B=a\\x_Ax_B=-\left(2-a\right)\end{cases}}\)ta xét \(x_A+x_B-x_Ax_B=a+\left(2-a\right)=2\left(dpcm\right)\)
Đúng 0
Bình luận (0)
cho parabol (P): y=ax^2 (a>0) và đường thẳng (d): y=2x-a^2
a, tìm a để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A;B
b,Gọi Xa; Xb là hoành độ của 2 điểm A và B. tính giá trị nhỏ nhất của biểu thức Q=4/(Xa+Xb) + 1/(Xa.Xb)
Cho hàm số
y
x
3
-
3
x
+
2
có đồ thị (C). Biết rằng trên (C) có hai điểm
A
(
x
A
;
y
A
)
;
B
(
x
B
;
y
B
)
phân biệt sao cho các tiếp tuyến với (C) tại A,B có cùng hệ số...
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 có đồ thị (C). Biết rằng trên (C) có hai điểm A ( x A ; y A ) ; B ( x B ; y B ) phân biệt sao cho các tiếp tuyến với (C) tại A,B có cùng hệ số góc, đồng thời đường thẳng đi qua A và B vuông góc với đường thẳng x+y-5=0. Tính tổng x A + 2 x B + y A + 3 y B , biết x A > x B .
A. 8
B. 2
C. 6
D. 10
Cho hàm số y=x^2 có đò thị (P) và đường thẳng (d) đi qua điểm M(1;2)có hệ số k khác 0
a/ Chứng minh rằng với mọi giá trị của k khác 0 đường thẳng (d) cắt (P) tại hai điểm phân biệt A và B
b/ Gọi Xa và Xb là hoành dộ hai diểm A và B. Chứng minh rằng Xa - Xb -Xa.Xb -2 =0
Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình
y
1
2
x
2
và hai điểm A, B thuộc (P) có hoành độ lần lượt là
x
A
−
1
;
x
B
2
.a) Tìm tọa độ của hai điểm A, B.b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.c) Tính khoảng cách từ O (gốc tọa độ) đến đường thẳng (d).
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình y = 1 2 x 2 và hai điểm A, B thuộc (P) có hoành độ lần lượt là x A = − 1 ; x B = 2 .
a) Tìm tọa độ của hai điểm A, B.
b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.
c) Tính khoảng cách từ O (gốc tọa độ) đến đường thẳng (d).
a) Vì A, B thuộc (P) nên:
x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2 , B ( 2 ; 2 )
b) Gọi phương trình đường thẳng (d) là y = ax + b.
Ta có hệ phương trình:
− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1
Vậy (d): y = 1 2 x + 1 .
c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)
=> OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào ∆ vuông OCD, ta có:
1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5
Vậy khoảng cách từ gốc O tới (d) là 2 5 5 .
Đúng 0
Bình luận (0)
một trạm áp biến vầ một khu dân cư cách xa hai bờ sông tại hai điểm A và B.
tìm điểm C sao cho cột mắc dây điện từ trạm biến áp về cho khu dân cư để độ dài đường dây là ngắn nhất.