Cho tam giác ABC vuông tại A,có AH là đường cao. Tính cạnh AB biết rằng diện tích tam giác AHC là 4,25 và cạnh AC là 5,57

Những câu hỏi liên quan
Cho tam giác ABC vuông taiA ,có độ dài cạnh AB=3cm,cạnh AC=4cm.Gọi AH là đường cao của tam giác .Tính diện tích tam giác AHC
\(S_{AHC}=\dfrac{AH\cdot HC}{2}=\dfrac{2.4\cdot3.2}{2}=2.4\cdot1.6=3.84\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Xét \(\Delta ABC\) vuông tại A có
\(BC^2=AB^2+AC^2=25\)
\(\Rightarrow BC=5\left(cm\right)\)
AC\(^2\) = CH . CB = 5 CH
\(\Rightarrow CH=3,2\left(cm\right)\)
AB . AC = AH . BC \(\Rightarrow AH=2,4\)
Nên \(S_{AHC}=\dfrac{1}{2}.AH.CH=\dfrac{1}{2}.2,4.3,2=3,84\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ hE vuông góc với cạnh AC tại E. Biết AB 15cm, BC 25cm.1)Tính độ dài cạnh AC và diện tích tam giác ABC.2)Chứng minh tứ giác ADHE là hình chữ nhật.3)Trên tia đối của AC lấy điểm F sao cho AF AE. Chứng minh tứ giác AFDH là hình bình hành.4)Gọi K là điểm đối xứng của B qua A, gọi M là trung điểm của AH. Chứng minh CM vuông góc HK.
Đọc tiếp
Cho tam giác ABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ hE vuông góc với cạnh AC tại E. Biết AB = 15cm, BC = 25cm.
1)Tính độ dài cạnh AC và diện tích tam giác ABC.
2)Chứng minh tứ giác ADHE là hình chữ nhật.
3)Trên tia đối của AC lấy điểm F sao cho AF = AE. Chứng minh tứ giác AFDH là hình bình hành.
4)Gọi K là điểm đối xứng của B qua A, gọi M là trung điểm của AH. Chứng minh CM vuông góc HK.
1: AC=20cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{15\cdot20}{2}=150\left(cm^2\right)\)
2: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
3: Xét tứ giác AFDH có
AF//DH
AF=DH
Do đó: AFDH là hình bình hành
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A( AB>AC), đường cao AH. Gọi M là trung điểm của AB,AD là phân giác của góc BAH (D thuộc BH),MD cắt AH tại E. 1)Chứng minh rằng: 2 2 AB AC BH CH = 2)Tính độ dài AH biết diện tích các tam giác AHC và ABH lần lượt là 8,64 cm2 và 15,36cm2 . 3) Chứng minh rằng: CE//AD
Cho tam giác ABC vuông tại A( AB>AC), đường cao AH. Gọi M là trung điểm của AB,AD là phân giác của góc BAH (D thuộc BH),MD cắt AH tại E.
a)Chứng minh rằng: \(\dfrac{AB^2}{BH}=\dfrac{AC^2}{CH}\)
b)Tính độ dài AH biết diện tích các tam giác AHC và ABH lần lượt là 8,64 cm2 và 15,36cm2 .
c) Chứng minh rằng: CE//AD
a: Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC và AC^2=CH*BC
=>AB^2/AC^2=BH/CH
b: S AHC=8,64
=>1/2*AH*HC=8,64
=>AH*HC=17,28
S AHB=15,36
=>1/2*AH*HB=15,36
=>AH*HB=30,72
mà AH*HC=17,28
nên AH*AH*HB*HC=30,72*17,28
=>AH^2*AH^2=30,72*17,28
=>AH^4=530,8416
=>\(AH=\sqrt[4]{530.8416}=4.8\left(cm\right)\)
Đúng 1
Bình luận (2)
cho tam giác ABC vuông tại A. kẻ đường cao AH. Biết AB=15cm, AC=20cm.
a) chứng minh tam giác AHB và tam giác CAB là hai tam giác đồng dạng
b) tính BC, AH
c) gọi M là trung điểm cạch BC. tính diện tích tam gác AHM.
a) Xét ΔAHB và ΔCAB có
Góc B chung
Góc AHB= Góc A=90o
=> ΔAHB ∼ ΔCAB (gg)
b) Xét ΔABC có Góc A=90o
=> AB2 + AC2=BC2
=>152+202=BC2
=> BC=25 cm
ta lại có SΔABC =\(\dfrac{AB.AC}{2}=\dfrac{BC.AH}{2}\)
=>\(AB.AC=BC.AH=>15.20=25.AH\)=>AH=12cm
c) M là trung điểm của BC=> BM=\(\dfrac{1}{2}BC=\dfrac{1}{2}.25=12,5\) cm
Xét ΔABH có góc BHA=90o
=> HB2+AH2=AB2
=> BH2+122=152=> BH=9cm
ta có AH⊥BC => AH⊥BM ( M∈BC)
SΔAHM=SΔABM-SΔABH
=> SΔAHM=\(\dfrac{12.12,5}{2}-\dfrac{12.9}{2}=21cm^2\)
Đúng 1
Bình luận (0)
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B, C và H (h.16). a) Chứng minh rằng:
A
H
A
H
B
C
B
C
b) Áp dụng: Cho biết
A...
Đọc tiếp
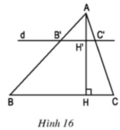
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H' (h.16).
a) Chứng minh rằng: A H ' A H = B ' C B C
b) Áp dụng: Cho biết A H ' A H = 1 3 và diện tích tam giác ABC là 67,5 cm2. Tính diện tích tam giác AB’C’.
a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒ 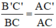
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒ 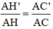
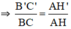
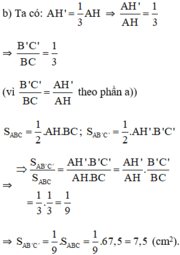
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB<AC, đường cao AH, phân giác góc HAC cắt HC tại D. Gọi I là điểm cách đều 3 cạnh của tam giác AHB, K là điểm cách đều 3 cạnh của tam giác AHC. Biết IK cắt AB và AC ở P và Q. Chứng minh AP=AQ
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B, C và H
a) Chứng minh rằng: .
b) Áp dụng: Cho biết và diện tích tam giác ABC là 67,5 cm2. Tính diện tích tam giác AB’C’.
Đọc tiếp
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H'
a) Chứng minh rằng: 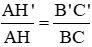
b) Áp dụng: Cho biết 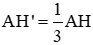
bài 5 cho tam giác ABC vuông tại A. kẻ đường cao AH. Biết AB=15cm, AC=20cm
a) Chứng minh tam giác AHB và tam giác CAB là hai tam giác đồng dạng
b) Tính BC, AH.
C) Gọi M là trung điểm cạnh BC. Tính diện tích tam giác AHM.
a) Xét ΔAHB và ΔCAB có
Góc B chung
Góc AHB= Góc A=90o
=> ΔAHB ∼ ΔCAB (gg)
Đúng 0
Bình luận (1)

















