Xác định vị trí điểm C để có hình thang ABCD, biết rằng:
Những câu hỏi liên quan
Xác định vị trí điểm C để có hình thoi ABCD.
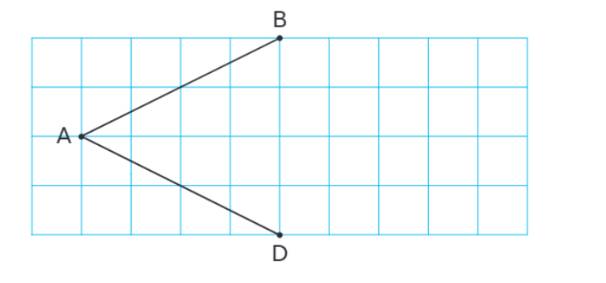
Xác định vị trí điểm C để có hình bình hành ABCD.
Cho hình chữ nhật ABCD. O là giao điểm hai đường chéo và một điểm P bất kì trên đường chéo BD (P nằm giữa O và D). Gọi M là điểm đối xứng của C qua P. a) Chứng minh tứ giác AMDB là hình thang. Xác định vị trí của P trên BD để AMDB là hình thang cân. b) Kẻ ME vuông góc AD, MF vuông góc BA. Chứng minh EF // AC và 3 điểm E, F, P thẳng hàng. c) Xác định vị trí P trên BD để tứ giác nối 4 điểm A, M, D, B là hình thang cân. d) Nếu hình chữ nhật ABCD có AB 2BC. Gọi K là điểm trên AB sao cho góc ADK $1...
Đọc tiếp
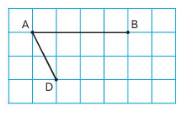
Cho hình chữ nhật ABCD. O là giao điểm hai đường chéo và một điểm P bất kì trên đường chéo BD (P nằm giữa O và D). Gọi M là điểm đối xứng của C qua P. a) Chứng minh tứ giác AMDB là hình thang. Xác định vị trí của P trên BD để AMDB là hình thang cân. b) Kẻ ME vuông góc AD, MF vuông góc BA. Chứng minh EF // AC và 3 điểm E, F, P thẳng hàng. c) Xác định vị trí P trên BD để tứ giác nối 4 điểm A, M, D, B là hình thang cân. d) Nếu hình chữ nhật ABCD có AB = 2BC. Gọi K là điểm trên AB sao cho góc ADK = $15^o$. Chứng minh tam giác CDK cân.
Cho hình thang ABCD (AB//CD) và AB < CD. Gọi E là điểm bất kỳ trên cạnh AB. Xác định vị trí điểm F trên cạnh CD để SAEFD v = SBCFE
Do hình thang AEFD và hình thang BCFE có cùng đường cao, suy ra S A E F D = S B C F E ⇔ D F = A B + D C 2 − A E
Cách dựng: Vẽ đường trung bình MN, trên đó lấy MK = AE. Từ K vẽ đường song song với BC cắt CD tại F cần tìm
Đúng 0
Bình luận (0)
Cho hình thang ABCD có 2 đáy là AB = 2a; CD = a. Hãy xác định vị trí điểm M trên đường thẳng CD sao cho Đường thẳng AM chia hình thang thành 2 phần có diện tích bằng nhau.
Cho hình thang ABCD có 2 đáy là AB = 2a; CD = a. Hãy xác định vị trí điểm M trên đường thẳng CD sao cho Đường thẳng AM chia hình thang thành 2 phần có diện tích bằng nhau.
Cho nửa đường tròn tâm O có đường kính AB.Vẽ các tiếp tuyến Ax và By theo thứ tự tại C và D.
A:C/M rằng dường tròn có dường kính CD tiếp xúc với AB.
B:Tìm vị trí M để hình thang ABCD có chu vi nhỏ nhất.
C:Tìm vị trí của C và D để hình thang ABCD có chu vi bằng 14cm,biết AB=4cm.
Cho HCN ABCD đường chéo AC và BD cắt nhau tại O.Lấy P là 1 điểm tùy ý trên OB.Gọi M là điểm đối xứng với C qua P. Từ M kẻ ME vuông góc với đường thẳng AB (F thuộc AB)
a) Chứng minh rằng AEFM là HCN
b) Chứng minh rằng AMBD là hình thang
c) Chứng minh E,F,P thẳng hàng
d) Xác định vị trí của P để AMBD là hình thang cân
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB. Gọi M,N lần lượt là trung điểm SA,SC; E = AC giao BD. Xác định vị trí tương đối của các cặp đường thẳng và mặt phẳng sau
a) MN và (ABCD)
b) AN và (ABD)
c) SE và (SAC)
a: Xét ΔSAC có M,N lần lượt là trung điểm của SA,SC
=>MN là đường trung bình của ΔSAC
=>MN//AC
mà MN không thuộc mp(ABCD) và \(AC\subset\left(ABCD\right)\)
nên MN//(ABCD)
b: \(A\in AN;A\in\left(ABD\right)\)
=>\(A\in AN\cap\left(ABD\right)\)
mà \(N\in SC\) không thuộc mp(ABD)
nên \(A=AN\cap\left(ABD\right)\)
c: \(S\in\left(SAC\right);E\in AC\subset\left(SAC\right)\)
Do đó: \(SE\subset\left(SAC\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, điểm H di chuyển trên BC, gọi E, F lần lượt là điểm đối xứng của H qua AB, AC
a) Chứng minh E, D, F thẳng hàng
b) Chứng minh BEFC là hình thang. Có thể tìm vị trí của H để BEFC thành hình thang vuông, hình bình hành, hình chữ nhật được không?
c) Xác định vị trí của H để EFH có diện tích lớn nhất