xác định dạng của số tự nhiên biểu thị tích sau
a) ab x101
b) ab x 7 x 11 x3
Xác định dạng của số tự nhiên biểu thị tích sau :
a) ab x 101
b) abc x 7 x 11 x3
xác định dạng của các tích sau :
a) ab x 101 ; b) abc x 7 x 11 x13
pé pun
a﴿ ab x 101 = ab x ﴾100 + 1﴿
= ab x 100 + ab x 1
= ab00 + ab
= abab
b﴿ abc x 7 x 11 x 13
= abc x 1001
= abc x ﴾1000 + 1﴿
= abc x 1000 + abc x 1
= abc000 + abc
= abcabc
Xác định dạng của các tích sau :
a) ab x 101
b) abc x 7 x 11 x 13
a / ab.101=ab(100+1)
= ab.100+ab.1
=ab00+ab
=abab
b/ abc.7.11.13=abc.1001
=abc(1000+1)
=abc.1000+abc.1
=abc000+abc=abcabc
a) ab x 101 = ab x (100 + 1)
= ab x 100 + ab x 1
= ab00 + ab
= abab
b) abc x 7 x 11 x 13
= abc x 1001
= abc x (1000 + 1)
= abc x 1000 + abc x 1
= abc000 + abc
= abcabc
xác định đường tiệm cận ngang của đồ thị hàm số sau
a) \(y=\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
b) \(y=\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
a: \(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{9+\dfrac{1}{x}}+1}{2+\dfrac{5}{x}}=\dfrac{\sqrt{9}+1}{2}=\dfrac{3+1}{2}=2\)
=>Đường thẳng y=2 là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{9+\dfrac{1}{x}}+1}{2+\dfrac{5}{x}}=\dfrac{-3+1}{2}=\dfrac{-2}{2}=-1\)
=>Đường thẳng y=-1 là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
b: \(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{2+\dfrac{1}{x^2}}-1}{1+\dfrac{2}{x}}=\dfrac{\sqrt{2}-1}{1}=\sqrt{2}-1\)
=>Đường thẳng \(y=\sqrt{2}-1\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{2+\dfrac{1}{x^2}}-1}{1+\dfrac{2}{x}}=\dfrac{-\sqrt{2}-1}{1}=-\sqrt{2}-1\)
=>Đường thẳng \(y=-\sqrt{2}-1\) là một tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
Xác định dạng các tích sau:
a)ab . 101 b)abc . 7 . 11 . 13
a / ab.101=ab(100+1)
= ab.100+ab.1
=ab00+ab
=abab
b/ abc.7.11.13=abc.1001
=abc(1000+1)
=abc.1000+abc.1
=abc000+abc=abcabc

\(a,\overline{ab}\cdot101=\overline{abab}\)
\(b,\overline{abc}\cdot7\cdot11\cdot13=\overline{abc\cdot1001}=\overline{abcabc}\)
Xác định dạng của tích sau:
a) ab . 101
b) abc . 7 . 11 .13
a) ab . 101 = ab . ( 100 + 1 )
= ab . 100 + ab
= ab00 + ab
= abab
b) abc . 7 . 11 . 13 = abc . 1001
= abc . ( 1000 + 1 )
= abc . 1000 + abc
= abcabc
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = x 3 - x , y = 2x và các đường thẳng được xác định bởi công thức.
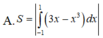
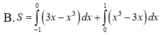
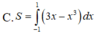
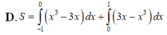
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = x 3 - x ; y = 2 x và các đường thẳng được xác định bởi công thức.
A. S = ∫ - 1 1 3 x - x 3 d x
B. S = ∫ - 1 0 3 x - x 3 d x + ∫ 0 1 x 3 - 3 x d x
C. S = ∫ - 1 1 3 x - x 3 d x
D. S = ∫ - 1 0 x 3 - 3 x d x + ∫ 0 1 3 x - x 3 d x
xác định dạng của các tích sau :
a) ab . 101
b) abc . 7 . 11. 13
ab.101
=abab
abc.7.11.13
=abc.(7.11.13)
=abc.1001
=abcabc
k nhé mọi người