a: \(\left|a-2b+3\right|^{2023}>=0\forall a,b\)

\(\left(b-1\right)^{2024}>=0\forall b\)

Do đó: \(\left|a-2b+3\right|^{2023}+\left(b-1\right)^{2024}>=0\forall a,b\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}a-2b+3=0\\b-1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=1\\a=2b-3=2\cdot1-3=-1\end{matrix}\right.\)

Thay a=-1 và b=1 vào P, ta được:

\(P=\left(-1\right)^{2023}\cdot1^{2024}+2024=2024-1=2023\)

a) Vì \(\left| {{u_n}} \right| = \left| 0 \right| = 0 < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim 0 = 0;\)

b) Vì \(0 < \left| {\frac{1}{{\sqrt n }}} \right| < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim \frac{1}{{\sqrt n }} = 0.\)

Xét biểu thức : \(\frac{1}{\sqrt{n}}=\frac{2}{\sqrt{n}+\sqrt{n}}>\frac{2}{\sqrt{n}+\sqrt{n+1}}=\frac{2\left(\sqrt{n+1}-\sqrt{n}\right)}{\left(\sqrt{n+1}\right)^2-\left(\sqrt{n}\right)^2}=2\left(\sqrt{n+1}-\sqrt{n}\right)\)với n > 0

Áp dụng : \(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2024}}>2\left(\sqrt{2}-\sqrt{1}+\sqrt{3}-\sqrt{2}+...+\sqrt{2025}-\sqrt{2024}\right)\)

\(\Rightarrow\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2024}}>2\left(\sqrt{2025}-1\right)=88\) (đpcm)

\(A=\dfrac{3}{1.4}+\dfrac{3}{2.6}+\dfrac{3}{3.8}+...............+\dfrac{1}{2012.1342}\)

\(A=\dfrac{3}{1.4}+\dfrac{3}{2.6}+\dfrac{3}{3.8}+...........................+\dfrac{3}{2012.4026}\)

\(A=\dfrac{6}{2.4}+\dfrac{6}{4.6}+\dfrac{6}{6.8}+..........................+\dfrac{6}{4024.4026}\)

\(A=3\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+\dfrac{2}{6.8}+...................+\dfrac{2}{4024.4026}\right)\)

\(A=3\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+....................+\dfrac{1}{4024}-\dfrac{1}{4026}\right)\)

\(A=3\left(\dfrac{1}{2}-\dfrac{1}{4026}\right)\)

\(A=3.\dfrac{1}{2}-3.\dfrac{1}{4026}\)

\(A=1,5-\dfrac{3}{4026}< 1,5\)

Ta có

A = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{2.6}\) + \(\dfrac{3}{3.8}\) + ... + \(\dfrac{1}{2012.1342}\)

A = \(\dfrac{3}{1.4}\) + \(\dfrac{3}{2.6}\) + \(\dfrac{3}{3.8}\) + ... + \(\dfrac{3}{2012.4026}\)

A = \(\dfrac{6}{2.4}\) + \(\dfrac{6}{4.6}\) + \(\dfrac{6}{6.8}\) + ... + \(\dfrac{6}{4024.4026}\)

A = \(3\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+\dfrac{2}{6.8}+...+\dfrac{2}{4024.4026}\right)\)

A = \(3\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{4024}-\dfrac{1}{4026}\right)\)

A = \(3\left(\dfrac{1}{2}-\dfrac{1}{4026}\right)\)

A = 3.\(\dfrac{1}{2}\) - 3.\(\dfrac{1}{4026}\)

A = 1,5 - \(3.\dfrac{1}{4026}\) < 1,5

=> A < 1,5

=> đpcm

Cô @Bùi Thị Vân hình như có gì đó nhầm lẫn!!

\(A=\)\(\frac{3}{1.4}\)\(+\)\(\frac{3}{2.6}\)\(+\)\(\frac{3}{2.8}\)\(+\).........\(+\)\(\frac{1}{2012.1342}\)\(< 1,5\)

\(=\)\(\frac{3}{1.4}\)\(+\)\(\frac{3}{2.6}\)\(+\)\(\frac{3}{3.8}\)\(+\)............\(+\)\(\frac{3}{2012.4026}\)

\(=\)\(\frac{6}{2.4}\)\(+\)\(\frac{6}{4.6}\)\(+\)\(\frac{6}{6.8}\)\(+\)..............\(+\)\(\frac{6}{4024.4026}\)

\(=\)\(3.\)\(\left(\frac{2}{2.4}+\frac{2}{4.6}+\frac{2}{6.8}+...........+\frac{2}{4024.4026}\right)\)

\(=\)\(3.\)\(\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+....+\frac{1}{4024}-\frac{1}{4026}\right)\)

\(=\)\(3.\)\(\left(\frac{1}{2}-\frac{1}{4026}\right)\)

\(=\)\(3.\)\(\frac{1}{2}\)\(-\)\(3.\)\(\frac{1}{4026}\)

\(=\)\(1,5\)\(-\)\(\frac{3}{4026}\)\(< \)\(1,5\)

Vậy \(A< 1,5\)

cứu tôi

what ?

10²⁰²⁴+2024 chính là số tự nhiên vì cả hai số đều là số tự nhiên :)

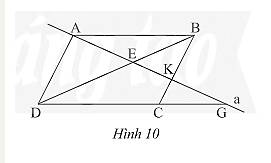
a) Vì \(ABCD\) là hình bình hành nên \(AB//CD;AD//BC\)

\( \Rightarrow AB//DG;AB//CG;BK//AD;KC//AD\)

Xét tam giác \(DEG\) có \(AB//DG\), theo hệ quả của định lí Thales ta có:

\(\frac{{AE}}{{EG}} = \frac{{EB}}{{ED}}\) (1)

Xét tam giác \(ADE\) có \(BK//AD\), theo hệ quả của định lí Thales ta có:

\(\frac{{EK}}{{AE}} = \frac{{EB}}{{ED}}\) (2)

Từ (1) và (2) suy ra, \(\frac{{AE}}{{EG}} = \frac{{EK}}{{AE}} \Rightarrow A{E^2} = EG.EK\) (điều phải chứng minh).

b) Xét tam giác \(AED\) có:

\(AD//BK \Rightarrow \frac{{AE}}{{AK}} = \frac{{DE}}{{DB}}\)(3)

Xét tam giác \(AEB\) có

\(AB//BK \Rightarrow \frac{{AE}}{{AG}} = \frac{{BE}}{{BD}}\) (4)

Từ (3) và (4) ta được:

\(\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = \frac{{DE}}{{BD}} + \frac{{BE}}{{BD}} = \frac{{BD}}{{BD}} = 1\)

Ta có: \(\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = 1 \Rightarrow \frac{1}{{AE}} = \frac{1}{{AK}} + \frac{1}{{AG}}\) (chia cả hai vế cho \(AE\)) (điều phải chứng minh).

2023 mũ 2024+2024 mũ 2025+2025 mũ 2026

Xét 2023 mũ 2024

\(^{2023^{2024}}\)=\(^{2023^{4.501}}\)=(\(^{2023^4}\))\(^{^{501}}\)

Ta có:\(^{2023^4}\)tận cùng là 1

=>2023 mũ 4 tất cả mũ 501 tận cùng là 1

Xét 2024 mũ 2025

2024 mũ 2025=2024 mũ 2 .1012+1=2024 mũ 2.1012 nhân 2024=(2024 mũ 2)mũ 1012.2024

Ta có:2024  mũ 2 tận cùng là 6

=>(2024 mũ 2) tất cả mũ 1012 tận cùng là 6

=>(2024 mũ 2) tất cả mũ 1012 nhân 2024 tận cùng là4

Xét 2025 mũ 2026

2025 mũ 2026

 5 mũ bao nhiêu thì chữ số tận cùng vẫn là 5

=>2025 mũ 2026 tận cùng là 5

Vậy tổng của các chữ số tận cùng là:1+4+5=10 chia hết cho 10

=> Tổng của 2023 mũ 2024+2024 mũ 2025+2025 mũ 2026 chia hết cho 10

Đây là bài áp dụng tính chất tìm chữ số tận cùng

Chúc bn học tốt

\(2023^{2024}+2024^{2025}+2025^{2026}\equiv\left(-1\right)^{1012}+\left(-1\right)^{2025}+0\equiv0\)(mod 5)

-> chia hết cho 5

Dễ dàng nhận thấy \(2023^{2024}+2025^{2026}\) là số chẵn mà \(2024^{2025}\)cũng là số chẵn nên chia hết cho 2

Do (2,5) = 1 nên chia hết cho 10