∠MHC
Những câu hỏi liên quan
2 tháng 5 2022 lúc 18:38
Cho:
Xét ∆MHC và ∆MKB có:
- góc BMK = góc MHC (đối đỉnh)
- MB = MC (cạnh huyền)
- BKM = MHC = 90°
2 tam giác trên bằng nhau theo trường hợp nào???
2 tam giác bằng nhau theo trường hợp cạnh huyền-góc nhọn
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho Mhc=40(g). % KL oxit là : 60% .Lập CT oxit và gọi tên
Gọi CTHH của oxit là $R_xO_y$
$\%R = \dfrac{xR}{40}.100\% = 60\%$
$\Rightarrow R = 24x(2)$
Với x = 1 thì R = 24(Mg)$
Vậy oxit là $MgO$
Đúng 2
Bình luận (0)
2) Lập CTHH:biết thành phần phần trăm là
57,5% Na; 40% O; 2,5% H và Mhc=40g
GTDC
Cho tam giác ABC vuông ở A, AB < AC, đường cao AH, trên cạnh AC lấy E sao cho AE=AB, gọi M là trung điểm của BE.Tính góc MHC
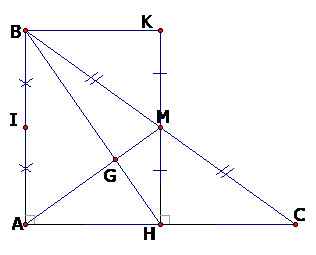
Cho ∆ABC vuông tại A, vẽ trung tuyến AM (M thuộc BC). Từ M kẻ MHvuông góc AC, trên tia đối của tia MH lấy điểm K sao cho MK = MH.
a) Chứng minh ∆MHC = ∆MKB.
b) Chứng minh AB // MH.
a) Xét ΔMHC và ΔMKB có
MH=MK(gt)
\(\widehat{CMH}=\widehat{BMK}\)(hai góc đối đỉnh)
MC=MB(M là trung điểm của BC)
Do đó: ΔMHC=ΔMKB(c-g-c)
b) Ta có: HM⊥AC(gt)
AB⊥AC(gt)
Do đó: HM//AB(Định lí 1 từ vuông góc tới song song)
Đúng 1
Bình luận (0)
cho tam giác abc vuông tại a có góc b bằng 68 độ trên BC lấy điểm K sao cho BA=BK.Qua điểm K vẽ đường vuông góc BC cắt AC tại M,cắt BA tại H.Chứng minh MHC tam giác cân
Xét ΔMAB vuông tại A và ΔMKB vuông tại K có
MB chung
BA=BK(gt)
Do đó: ΔMAB=ΔMKB(cạnh huyền-cạnh góc vuông)
Suy ra: MA=MK(Hai cạnh tương ứng)
Xét ΔMAH vuông tại A và ΔMKC vuông tại K có
MA=MK(cmt)
\(\widehat{AMH}=\widehat{KMC}\)(hai góc đối đỉnh)
Do đó: ΔMAH=ΔMKC(cạnh góc vuông-góc nhọn kề)
Suy ra: MH=MC(Hai cạnh tương ứng)
Xét ΔMHC có MH=MC(cmt)
nên ΔMHC cân tại M(Định nghĩa tam giác cân)
Đúng 0
Bình luận (0)
Cho một mạch dao động điện từ gồm 1 tụ điện có điện dung 4 (μF). Biết tần số dao động của từ trường trong cuộn cảm là 2653 Hz. Xác định độ tự cảm
A.0,9 mH
B.3,6 mH
C.3,6 H
D.0,09 H
Cho tam giác ABC có đường cao AH = 5cm , đáy BC = 6 cm , gọi M là trung điểm của AC , nối MH được tứ giác ABHM có diện tích gấp đôi diện tích tam giác MHC . Tính diện tích hình MBH .
Cho (O) , 2 đường kính AB, MN vuông góc . Trên tia AM lấy C. Kẻ MH \(\perp\) BC, MB cắt OH tại E. Gọi giao điểm của (O) và đường trong ngoại tiếp tam giác MHC là K. CMR : C, K, E thẳng hàng.
GỢI Ý:
*Bản chất câu hỏi của bài toán là chứng minh N,E,C thẳng hàng.
*Chứng minh AMBN là hình vuông \(\Rightarrow\widehat{OMB}=\widehat{OBM}=45^0\).
*Chứng minh tứ giác OBHM nội tiếp.
\(\Rightarrow\left\{{}\begin{matrix}\widehat{OMB}=\widehat{OHB}\\\widehat{OBM}=\widehat{OHM}\end{matrix}\right.\)
Suy ra ME là phân giác của tam giác BHM.
\(\Rightarrow\dfrac{ME}{BE}=\dfrac{MH}{BH}\)
△MHB∼△CMB nên \(\dfrac{MH}{BH}=\dfrac{CM}{BM}\)
\(\Rightarrow\dfrac{ME}{BE}=\dfrac{CM}{BM}=\dfrac{CM}{BN}\)
\(\Rightarrow\)△CME∼△NBE (c-g-c).
\(\Rightarrow\widehat{CEM}=\widehat{NEB}\) nên C,E,N thẳng hàng.
*NC cắt (O) tại D. \(\Rightarrow\widehat{MDN}=90^0=\widehat{MDC}\)
\(\Rightarrow\)Tứ giác MDHC nội tiếp
\(\Rightarrow\)D thuộc đường tròn ngoại tiếp tam giác MHC nên D trùng K.
\(\Rightarrowđpcm\)
Đúng 2
Bình luận (0)
Cho tam giác ABC nhọn có AB = AC.Gọi H là trung điểm của BC
a) Chứng minh \(\Delta\)AHB = \(\Delta\)AHC và AH \(\perp\) BC
b) Trên tia đối của tia HA lấy điểm M sao cho HM = HA.Chứng minh \(\Delta\)AHB = \(\Delta\)MHC và MC // AB
\(a,\left\{{}\begin{matrix}AB=AC\\BH=HC\\AH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AHB=\Delta AHC\left(c.c.c\right)\\ \Rightarrow\widehat{AHB}=\widehat{AHC}\\ \text{Mà }\widehat{AHB}+\widehat{AHC}=180^0\\ \Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\\ \Rightarrow AH\perp BC\\ b,\left\{{}\begin{matrix}HM=HA\\\widehat{AHB}=\widehat{MHC}\left(đđ\right)\\BH=HC\end{matrix}\right.\Rightarrow\Delta AHB=\Delta MHC\left(c.g.c\right)\\ \Rightarrow\widehat{HBA}=\widehat{HCM}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}MC\)
Đúng 1
Bình luận (0)