bip bip

Những câu hỏi liên quan
1 thiet bi dien tu phat tieng keu bip sau 60 giay 1 thiet bi dien tu khac cung phat ra tieng keu bip sau 62 giay luc 10 gio sang 2 thiet bi cung keu hoi sau bao lau 2 thiet bi lai phat cung nhau
Gọi thiết bị điện tử thứ nhất là a và thiết bị điện tử thứ 2 là b
Phân tích ra thừ số nguyên tố
\(60=2^2.3.5\)
\(62=2.31\)
BCNN ( a;b ) = \(2^2.3.5.31=1860\)giây
Vậy sau 1860 giây thì 2 thiết bị sẽ cùng kêu
Đúng 0
Bình luận (0)
Ta có : 60 = 22 . 3 . 5
62 = 31. 2
=> BCNN(60;62) = 22 . 3 . 5 .31 = 1860
Vậy cứ sau 1860 giây <=> 31 phút thì 2 thiết bị kêu cùng một lúc
Đúng 0
Bình luận (0)
Bài 10: Cho hình thang BPQC ( như hình vẽ).
a) So sánh diện tích tam giác BIP và tam giác QIC.
b) Tính diện tích BPQC biết AP 1/3 AB và diện tích tam giác ABC 45 cm2.
Đọc tiếp
Bài 10: Cho hình thang BPQC ( như hình vẽ).
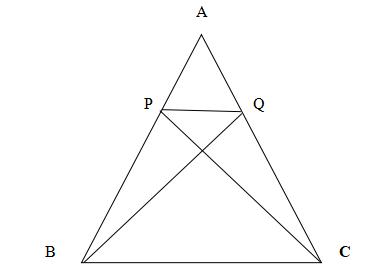
a) So sánh diện tích tam giác BIP và tam giác QIC.
b) Tính diện tích BPQC biết AP = 1/3 AB và diện tích tam giác ABC= 45 cm2.
a/
Hai tg BPQ và tg CQP có đường cao từ B->PQ = đường cao từ C->PQ
Cạnh đáy PQ chung
\(\Rightarrow S_{BPQ}=S_{CQP}\)
Hai tg trên có phần diện tích chung là \(S_{IPQ}\Rightarrow S_{BIP}=S_{QIC}\)
b/
Hai tg ACP và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{ACP}}{S_{ABC}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{ACP}=\dfrac{1}{3}xS_{ABC}\)
Hai tg ACP và tg ABQ có phần diện tích chung là \(S_{APIQ}\)
Mà \(S_{BIP}=S_{QIC}\Rightarrow S_{ACP}=S_{ABQ}=\dfrac{1}{3}xS_{ABC}\)
Hai tg APQ và tg ABQ có chung đường cao từ Q->AB nên
\(\dfrac{S_{APQ}}{S_{ABQ}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{APQ}=\dfrac{1}{3}xS_{ABQ}=\dfrac{1}{3}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{9}xS_{ABC}\)
\(\Rightarrow S_{BPQC}=S_{ABC}-S_{APQ}=S_{ABC}-\dfrac{1}{9}xS_{ABC}=\dfrac{8}{9}xS_{ABC}=\dfrac{8}{9}x45=40cm^2\)
Đúng 2
Bình luận (0)
Choose the word that doesn't belong to the gruop
1A.easy B.peaceful C.simple D.clever
2.A.friendly B.delicious c.awful D.hot
3.Asymbol B. Bip Ben Ceiffel tower D.the sttue of the Liberty
Choose the word that doesn't belong to the gruop
1A.easy B.peaceful C.simple D.clever
2.A.friendly B.delicious c.awful D.hot
3.Asymbol B. Bip Ben Ceiffel tower D.the sttue of the Liberty
minh nghi cau 2 la friendly
Xem thêm câu trả lời
Cho tam giác ABC có AB <AC.Vẽ phân giác AD của tam giác ABC .Tìm cạnh AC lấy điểm E sao cho AE= AB. CM
a) tam giác ADB= tam giác ADE
b)AP là dường trung trực của BE
c) Ab cát DE tại F . CM tam giác BIP= Tam giác FCP
Cho tam giác ABC có AB <AC.Vẽ phân giác AD của tam giác ABC .Tìm cạnh AC lấy điểm E sao cho AE= AB. CM
a) tam giác ADB= tam giác ADE
b)AP là dường trung trực của BE
c) Ab cát DE tại F . CM tam giác BIP= Tam giác FCP
a: Xét ΔADB và ΔADE có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó:ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên AB=AE và DB=DE
=>AD là đường trung trực của BE
c: Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)
Do đó; ΔDBF=ΔDEC
Đúng 0
Bình luận (0)
Cho tam giác ABC,AP bằng 1/3 AB.Biết PQCB là hình thang.Đường chéo QB và PC cắt nhau tại I.
a)So sánh diện tích tam giác BIP và CIQ.
b)tính diện tích hình thang PQCB biết diện tích tam giác ABC là 45 cm2
Giải ra cho mình luôn nhé!Vì đây là bài hình các bạn nhớ lập luận cho chặt chẽ nha.
Ai có câu trả lời sớm nhất mình cho 2 tick
Cho tam giác ABC đều có O là trọng tâm . Gọi M thuộc BC vẽ MP vuông góc AB tại P , MQ vuông góc AC tại Q . MP cắt OB ở I ; MQ cắt OC ở K ; IK cắt OM ở S
1) CM : MIOK là hình bình hành , suy ra S là trung điểm của IK
2) Tam giác BIM và tam giác CKM là các tam giác cân
3) Tam giác BIP đồng dạng với tam giác CKQ suy ra frac{CK}{KQ}frac{BI}{IP}
4) IK // PQ
5) PQ cắt OM ở R . Chứng minh R là trung điểm của PQ
HELP ME !!!
Đọc tiếp
Cho tam giác ABC đều có O là trọng tâm . Gọi M thuộc BC vẽ MP vuông góc AB tại P , MQ vuông góc AC tại Q . MP cắt OB ở I ; MQ cắt OC ở K ; IK cắt OM ở S
1) CM : MIOK là hình bình hành , suy ra S là trung điểm của IK
2) Tam giác BIM và tam giác CKM là các tam giác cân
3) Tam giác BIP đồng dạng với tam giác CKQ suy ra \(\frac{CK}{KQ}=\frac{BI}{IP}\)
4) IK // PQ
5) PQ cắt OM ở R . Chứng minh R là trung điểm của PQ
HELP ME !!!
cho hình vẽ sau:Cho biết BPQC là hình thang.a)So sánh diện tích tam giác BIP và diện tích tam giác CIQb) Tính diện tích hình thang BPQC biết AP1/3 AB và diện tích tam giác ABC là 45cm2 A C B P Q i
Đọc tiếp
cho hình vẽ sau:Cho biết BPQC là hình thang.
a)So sánh diện tích tam giác BIP và diện tích tam giác CIQ
b) Tính diện tích hình thang BPQC biết AP=1/3 AB và diện tích tam giác ABC là 45cm2
Xem thêm câu trả lời
Xem thêm câu trả lời
























