Cho đường thẳng (d) : y = 2x + 3
a) Tính khoảng cách từ điểm A(1; 2) đến đường thẳng (d)
b) Tính diện tích tam giác tạo bởi (d) với các trục tọa độ
c) Viết phương trình đường thẳng (∆) đi qua A sao cho khoảng cách từ O đến ∆ là lớn nhất, nhỏ nhất
Những câu hỏi liên quan
Bài 5: Cho (d): y = -2x + 3
a) Tìm tọa độ giao điểm A, B của ĐTHS lần lượt với Ox, Oy
b) Tính khoảng cách từ gốc tọa độ đến đường thẳng (d)
c) Tính khoảng cách từ C(0; -2) đến đường thẳng (d)
\(a,\) Pt hoành độ giao điểm
\(x=0\\ \Leftrightarrow y=-2\cdot0+3=3\\ \Leftrightarrow A\left(0;3\right)\)
Pt tung độ giao điểm
\(y=0\\ \Leftrightarrow0=-2x+3\Leftrightarrow x=\dfrac{3}{2}\\ \Leftrightarrow B\left(\dfrac{3}{2};0\right)\)
Đúng 2
Bình luận (0)
cho đường thẳng (d) y=-4x+3
a, vẽ độ thị hàm số độ cho
b, tìm tọa độ điểm A,B của d với lận lượt vơi 2 trục tọa độ Ox và Oy
c, tính khoảng cách từ góc tọa độ đến (d )
d, tính khoảng cách từ I (-1,-2) để d
e, tính diên tích tam giác OAB
Cho đường thẳng (d): y = -2x + 3. Xác định tọa độ giao điểm A;B của đường thẳng (d) với hai trục Ox, Oy. Tính khoảng cách từ điểm O(0;0) đến đường thẳng (d)
* Giao điểm với trục Ox:
Ta có: -2x + 3 = 0
⇔ 2x = 3
⇔ x = 3/2
⇒ A(3/2; 0) là giao điểm với trục Ox
* Giao điểm với trục Oy:
x = 0 ⇔ y = 3
⇒ B(0; 3) là giao điểm với trục Oy
* Khoảng cách từ O(0; 0) tới (d):
Xét đồ thị:
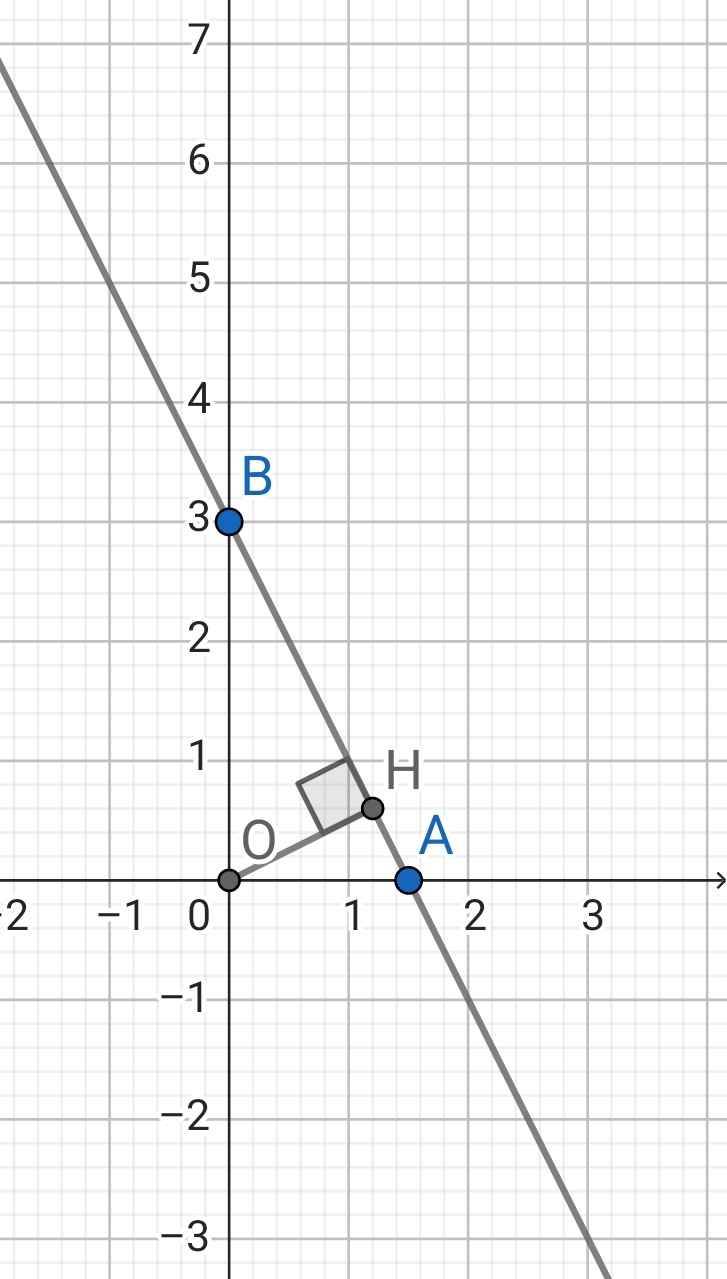Ta có:
AB² = OA² + OB² (Pytago)
= (3/2)² + 3²
= 45/4
⇒ AB = 3√5/2
Khoảng cách từ O đến (d) là đoạn thẳng OH
Ta có:
OH.AB = OA.OB
⇒ OH = OA.OB : AB
= 3/2 . 3 : (3√5/2)
= 3/√5
Đúng 3
Bình luận (0)
khoảng cách là \(\dfrac{3}{\sqrt{5}}\)
Đúng 0
Bình luận (0)
Bài 1: Cho đường thẳng d : y= -4x+3
a) Vẽ đồ thị hàm số đã cho
b) Tìm tọa độ giao điểm A,B của d với hai trục Ox và Oy
c) Tính khoảng cách từ gốc tọa độ O đến d
GIÚP MIK VỚIIIII
1) Tính khoảng cách từ điểm M đến đường thẳng d, với:
M(3,5); (d): x + y + 1 =0
M(2,3); (d): {x-2t, y = 2 + 3t
M(2,-3); (d): (x - 2)/2 = ( y + 1)/3
2) Viết phưởng trình đường thẳng d song song với đường thẳng △: 2x - y +3 =0 và cách △ một khoảng bằng căn 5
\(1/\)
\(M\left(3;5\right);d:x+y+1=0\)
\(\)Gọi khoảng cách từ M đến d là \(l\)
\(l\left(M;d\right)=\dfrac{\left|x_M+y_M+1\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|3+5+1\right|}{\sqrt{1^2+1^2}}=\dfrac{9\sqrt{2}}{2}\)
\(M\left(2;3\right);d:\left\{{}\begin{matrix}x-2t\\y=2+3t\end{matrix}\right.\)
d qua \(M\left(2;3\right)\) có \(VTCP\overrightarrow{u}=\left(-2;3\right)\Rightarrow VTPT\overrightarrow{n}=\left(3;2\right)\)
\(PTTQ\) của \(\Delta:3\left(x-2\right)+2\left(y-3\right)=0\)
\(\Rightarrow3x-6+2y-6=0\)
\(\Rightarrow3x+2y-12=0\)
Gọi khoảng cách từ M đến d là \(l\)
\(l\left(M;d\right)=\dfrac{\left|3.x_M+2.y_M-12\right|}{\sqrt{3^2+2^2}}=\dfrac{\left|3.2+2.3-12\right|}{\sqrt{3^2+2^2}}=0\)
Đúng 2
Bình luận (0)
Cho đường thẳng d hàm số y= ax + 3a +2
a. Xác định a để đường thẳng d cắt trục hoành tại điểm có hoành độ x= -1. Tính khoảng cách từ gốc tọa độ đến đường thẳng d với a
b. Cmr với mọi a họ đường thẳng xã định B luôn đi qua điểm cố định
c. Tìm a để đường thẳng d tạo 2 trục tọa độ 1 tam giác S =1
Cho hàm số (d):y=-x-3
a) Vẽ đồ thị hàm số (d) trên hệ trục tọa độ Oxy.
b) Gọi A, B lần lượt là giao điểm của đường thẳng (d) với trục tung và trục hoành.
Tính chu vi và diện tích tam giác AOB.
c) Tính khoảng cách từ gốc tọa độ O đến đường thẳng (d)
Trong mặt phẳng tọa độ Oxy, cho điểm K(1;1) và đường thẳng (Δ) có phương trình \(y=2x+\sqrt{3}\). Gọi (d) là 1 đường thẳng song song với đường thẳng (Δ) có và cắt trục tung tại điểm có tung độ bằng 1. Hãy tính khoảng cách từ K đến đường thẳng (d)
Gọi \(\left(d\right):y=ax+b\) là đt của (d)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne\sqrt{3}\\b=1\end{matrix}\right.\Leftrightarrow\left(d\right):y=2x+1\Leftrightarrow2x-y+1=0\)
Khoảng cách từ K đến (d) là \(d\left(K;d\right)=\dfrac{6\cdot1-1+1}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)
Đúng 0
Bình luận (0)
cho đường thẳng (d): y=m(2x-1)+3-2x
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) bằng 1.
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) đạt giá trị lớn nhất.