y² = x tìm những điểm thuộc (P) cách đều tiêu điểm F một khoảng bằng 3

Những câu hỏi liên quan
Một điểm M thuộc parabol (P): y 2 = x. Nếu khoảng cách từ M đến tiêu điểm F của (P) bằng 1 thì hoành độ của điểm M bằng bao nhiêu?
A. 3/4
B. 3 /2
C. 3
D. 3
Đáp án: A
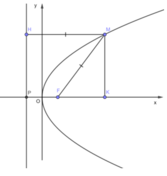
(P): y 2 = x ⇒ p = 1/2
Ta có:
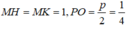
Hoành độ của điểm M chính là độ dài đoạn OK
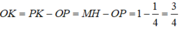
Đúng 0
Bình luận (0)
Cho hàm số y = x + 2 x - 3 có đồ thị (C). Có bao nhiêu tiêu điểm thuộc sao cho khoảng cách từ điểm đến tiệm cận ngang bằng 5 lần khoảng cách từ điểm đến tiệm cận đứng.
A. 1
B. 2
C. 3
D. 4
cho ham so y=f(x)=x^2(P)
? Tìm trên P những điểm có khoảng cách đến gốc tọa độ bằng căn 2
Lấy \(M\left(a,a^2\right)\in\left(P\right),a\inℝ\).
\(MO=\sqrt{a^2+a^4}=\sqrt{2}\)
\(\Leftrightarrow a^4+a^2=2\)
\(\Leftrightarrow a^4+a^2+\frac{1}{4}=\frac{9}{4}\)
\(\Leftrightarrow\left(a^2+\frac{1}{2}\right)^2=\left(\frac{3}{2}\right)^2\)
\(\Leftrightarrow\orbr{\begin{cases}a^2+\frac{1}{2}=\frac{3}{2}\\a^2+\frac{1}{2}=-\frac{3}{2}\end{cases}}\Leftrightarrow a^2=1\Leftrightarrow a=\pm1\).
Vậy ta có hai điểm thỏa mãn yêu cầu bài toán là \(\left(-1,1\right)\)và \(\left(1,1\right)\).
Một thấu kính hội tụ có tiêu cự 30cm . Khoảng cách giữa hai tiêu điểm F và F bằng bao nhiêu?
Vì F và F' đối xứng với nhau qua quang tâm O
\(\Rightarrow FF'=2OF=2OF'=2.30=60\left(cm\right)\)
Vậy khoảng cách giữa 2 tiêu điểm là 60cm
Đúng 1
Bình luận (0)
Một (E) có độ dài trục lớn bằng 6, tâm sai bằng \(\dfrac{1}{2}\), khoảng cách từ M thuộc (E) đến tiêu điểm F1 (có hoành độ âm) bằng 7.
a. Tìm khoảng cách từ M đến F2
b. Viết PTCT (E) và tìm M
Bài 1: Cho hàm số y=f(x)=ax4-bx2+x+3. Biết f(2)=17. Tính f(-2)
Bài 2: Cho(d):y=-x+2
a) Vẽ (d)
b) Tìm các điểm nằm trên (d) sao cho khoảng cách từ điểm đó đến trục Ox bằng 2 làn khoảng cách từ đó đến trục Oy
Điểm M (x;y)thuộc đường thẳng y= 2x+1 và cách trục hoành một khoảng = 3 . Tìm toạn độ điểm M
Vì M cách trục hoành một khoảng = 3 => \(\orbr{\begin{cases}y_m=3\\y_m=-3\end{cases}}\)
* Với \(y_m=3\Rightarrow x_m=\frac{3-1}{2}=1\)=> \(M_1(1;3)\)
* Với \(y_m=-3\Rightarrow x_m=\frac{-3-1}{2}=-2\)=> \(M_2(-2;-3)\)
Đúng 0
Bình luận (0)
Cho parabol (P) có tiêu điểm F và đường chuẩn Delta . Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên p 0Chọn hệ trục tọa độ Oxy sao cho Fleft( {frac{p}{2};0} right) và Delta :x + frac{p}{2} 0Xét điểm M(x;y)a) Tính MF và dleft( {M,Delta } right)b) Giải thích biểu thức sau:M(x;y) in (P) Leftrightarrow sqrt {{{left( {x - frac{p}{2}} right)}^2} + {y^2}} left| {x + frac{p}{2}} right|
Đọc tiếp
Cho parabol (P) có tiêu điểm F và đường chuẩn \(\Delta \). Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên \(p > 0\)
Chọn hệ trục tọa độ Oxy sao cho \(F\left( {\frac{p}{2};0} \right)\) và \(\Delta :x + \frac{p}{2} = 0\)
Xét điểm \(M(x;y)\)
a) Tính MF và \(d\left( {M,\Delta } \right)\)
b) Giải thích biểu thức sau:
\(M(x;y) \in (P) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\)
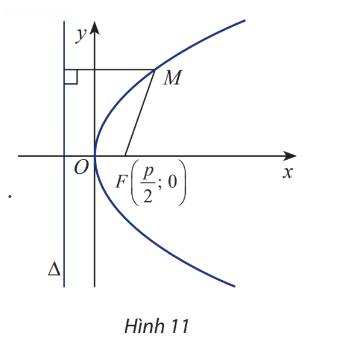
a) Ta có: \(\overrightarrow {FM} = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} \)
\(d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|\)
b) M thuộc parabol (P) nên M cách đều F và \(\Delta \)
Suy ra \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x - \frac{p}{2}} \right|\)
Đúng 0
Bình luận (0)
Cho đường thẳng d: y=x-5
a) Tìm các điểm M thuộc trục Ox sao cho khoảng cách từ M đến đường thẳng d bằng 2.
b) Tìm các điểm N thuộc trục Oy sao cho khoảng cách từ N đến đường thẳng d bằng 2.
Biết đường thẳng y(3m-1)x+6m+3 cắt đồ thị hàm số
y
x
3
-
3
x
2
+
1
tại 3 điểm phần biệt sao cho có một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây? A. (-1;0) B. (0;1)
C
.
1
;
3
2
D...
Đọc tiếp
Biết đường thẳng y=(3m-1)x+6m+3 cắt đồ thị hàm số y = x 3 - 3 x 2 + 1 tại 3 điểm phần biệt sao cho có một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?
A. (-1;0)
B. (0;1)
C . 1 ; 3 2
D . 3 2 ; 2

















