Đáp án: A
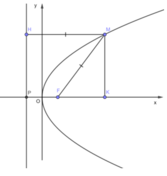
(P): y 2 = x ⇒ p = 1/2
Ta có:
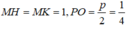
Hoành độ của điểm M chính là độ dài đoạn OK
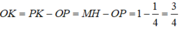
Đáp án: A

(P): y 2 = x ⇒ p = 1/2
Ta có:
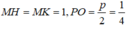
Hoành độ của điểm M chính là độ dài đoạn OK
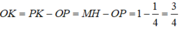
Một điểm A thuộc parabol (P): y 2 = 4x. Nếu khoảng cách từ A đến đường chuẩn bằng 5 thì khoảng cách từ A đến trục hoành bằng bao nhiêu?
A. 3
B. 5
C. 8
D. 4
Cho Elip (E) x 2 16 + y 2 12 = 1 và điểm M nằm trên (E) . Nếu điểm M có hoành độ bằng 1 thì các khoảng cách từ M tới 2
tiêu điểm của (E) bằng
A. 4 ± 2
B. 3 và 5.
C. 3,5 và 4,5
D. 4 ± 2 2
Một (E) có độ dài trục lớn bằng 6, tâm sai bằng \(\dfrac{1}{2}\), khoảng cách từ M thuộc (E) đến tiêu điểm F1 (có hoành độ âm) bằng 7.
a. Tìm khoảng cách từ M đến F2
b. Viết PTCT (E) và tìm M
Cho hàm số y=x²-mx-3(1) a/Tìm m để đồ thị hàm số (1) cắt Õ tại điểm có hoành độ bằng 3 b/lập bảng biến thiên và vẽ đồ thị khi m=-2 c/Tìm tọa độ giao điểm (P) với đường thẳng (d)y=2x+9 d/tìm m để parabol của hàm số có đỉnh nằm trên trục Ox
Cho elip E : x 2 169 + y 2 144 = 1 và điểm M nằm trên (E). Nếu M có hoành độ bằng - 13 thì khỏang cách từ M đến hai tiêu điểm bằng
A. 10 và 6.
B. 8 và 18.
C. 13 ± 5 .
D. 13 ± 10 .
Cho hàm số y = f(x) = mx + 2m − 3 có đồ thị (d). gọi A, B là hai điểm thuộc đồ thị
và có hoành độ lần lượt là −1 và 2.
1 Xác định tọa độ hai điểm A và B.
2 Tìm m để cả hai điểm A và B cùng nằm phía trên trục hoành.
3 Tìm điều kiện của m để f(x) > 0, ∀x ∈ [−1; 2]
Câu 1: Tìm tập hợp các điểm cách đều 2 đường thẳng:
Delta3 :3x + 4 y + 6 = 0
Delta4 :5x -10 = 0 ( phân giác góc tạo bởi D3 và D4 )
Câu 2: Cho hai đường thẳng:
Delta : 3x + 2y - 1 = 0 và d : 5x - 3y+2=0
1) Tính khoảng cách từ A(5 ;4) đến đường thẳng Delta
2) Viết phương trình các đường phân giác của góc tạo bởi hai đường thẳng trên.
3) Tìm điểm M thuộc Delta sao cho khoảng cách từ M đến d bằng 5.
4) Tìm điểm N thuộc đường thẳng (D1) : x - 2y = 0 bằng hai lần khoảng cách từ N đến d .
Trong mặt phẳng tọa độ Oxy, tìm điểm M thuộc trục hoành để khoảng cách từ đó đến điểm N(- 1; 4) bằng 2 5 .
A. M(1; 0)
B.M(1; 0); M(- 3; 0)
C.M( 3; 0)
D. M(1; 0); M(3; 0)
1) Tính khoảng cách từ điểm M đến đường thẳng d, với:
M(3,5); (d): x + y + 1 =0
M(2,3); (d): {x-2t, y = 2 + 3t
M(2,-3); (d): (x - 2)/2 = ( y + 1)/3
2) Viết phưởng trình đường thẳng d song song với đường thẳng △: 2x - y +3 =0 và cách △ một khoảng bằng căn 5