Đáp án: D
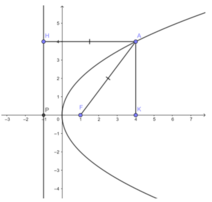
Ta có: (P) y 2 = 4x ⇒ F(1;0) ⇒ PF = 2
PK = AH = 5 ⇒ FK = 5 - 2 = 3
Mà AF = AH = 5
Xét tam giác vuông AKF có:
A K 2 = A F 2 - F K 2 = 5 2 - 3 2 = 16 ⇒ AK = 4
Vậy khoảng cách từ A đến trục hoành bằng 4
Đáp án: D

Ta có: (P) y 2 = 4x ⇒ F(1;0) ⇒ PF = 2
PK = AH = 5 ⇒ FK = 5 - 2 = 3
Mà AF = AH = 5
Xét tam giác vuông AKF có:
A K 2 = A F 2 - F K 2 = 5 2 - 3 2 = 16 ⇒ AK = 4
Vậy khoảng cách từ A đến trục hoành bằng 4
Một điểm M thuộc parabol (P): y 2 = x. Nếu khoảng cách từ M đến tiêu điểm F của (P) bằng 1 thì hoành độ của điểm M bằng bao nhiêu?
A. 3/4
B. 3 /2
C. 3
D. 3
Một (E) có độ dài trục lớn bằng 6, tâm sai bằng \(\dfrac{1}{2}\), khoảng cách từ M thuộc (E) đến tiêu điểm F1 (có hoành độ âm) bằng 7.
a. Tìm khoảng cách từ M đến F2
b. Viết PTCT (E) và tìm M
Trong mặt phẳng Oxy, cho hai điểm A(2;0) và B(6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại A và khoảng cách từ tâm của (C) đến B bằng 5.
Phương trình chính tắc của parabol mà khoảng cách từ tiêu điểm đến đường chuẩn bằng 2.
A. y 2 = 2x
B. y 2 = 4x
C. 2 y 2 = x
D. y 2 = -x/2
Viết phương trình chính tắc của parabol mà khoảng cách từ tiêu điểm đến đường chuẩn bằng 2.
A. y 2 = 2 x
B. y 2 = 4 x
C. 2 y 2 = x
D. y 2 = - x 2
Câu 1: Tìm tập hợp các điểm cách đều 2 đường thẳng:
Delta3 :3x + 4 y + 6 = 0
Delta4 :5x -10 = 0 ( phân giác góc tạo bởi D3 và D4 )
Câu 2: Cho hai đường thẳng:
Delta : 3x + 2y - 1 = 0 và d : 5x - 3y+2=0
1) Tính khoảng cách từ A(5 ;4) đến đường thẳng Delta
2) Viết phương trình các đường phân giác của góc tạo bởi hai đường thẳng trên.
3) Tìm điểm M thuộc Delta sao cho khoảng cách từ M đến d bằng 5.
4) Tìm điểm N thuộc đường thẳng (D1) : x - 2y = 0 bằng hai lần khoảng cách từ N đến d .
Trong mặt phẳng tọa độ Oxy, tìm điểm M thuộc trục hoành để khoảng cách từ đó đến điểm N(- 1; 4) bằng 2 5 .
A. M(1; 0)
B.M(1; 0); M(- 3; 0)
C.M( 3; 0)
D. M(1; 0); M(3; 0)
Trong mặt phẳng với hệ tọa độ
Oxy, cho hai điểm A (2;0) , B (6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại điểm A và khoảng cách từ tâm của (C) đến
điểm B bằng 5.
Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau:
a, A(3; 5) và Δ : 4x + 3y +1 = 0
b, B(1; -2) và d: 3x – 4y -26 = 0
c, C(1; 2) và m: 3x + 4y -11 = 0