a) 4x+6=3x-4

<=>4x-3x=-4-6

<=>x=-10

a)Tìm x:

4x+6=3x-4

4x-3x=-4-6

       x=-10

Vậy x=-10

c)Tính nhanh:

2315.(-2314+1)-2314.(1-2315)

=2315.(-2314)+2315-2314-2314.2315

=2315.(-2314+1-2314)-2314

=2315.(-4627)-2314

=-10711505-2314

=-10713819

a, 4x + 6 = 3x - 4

=> 4x - 3x = - 4 - 6

=> 1x = -10

=> x = - 10

Vậy x = - 10

b, Vì IbI > 0 nên để IbI - b = 0 thì b cũng phải lón hơn 0

Vậy b > 0

c, 2315 . (-2314 +1 ) - 2314 . ( 1- 2315)

= 2315 . (- 2314) + 2315 . 1 - 2314 . 1 - 2314 . 2315

= 2315 . (- 2314 + 1 + 2314) - 2314 . 1

= 2315 . 1 -2314 . 1

= 1. ( 2315 - 2314)

=1. 1

=1

Ta có x = 1/2, y = 3/4

=> 1/2 = 2/4 ; 3/4 = 3/4

vì 2/4 < 3/4 nên x < y

\(\dfrac{1}{2}=0.5\)

\(\dfrac{3}{4}=0.75\)

mà 0,5<0,75

nên x<y

a: Ta có: \(\dfrac{1}{2}=0.5\)

\(\dfrac{3}{4}=0.75\)

mà 0,5<0,75

nên x<y

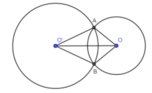
Vì số đo hai cung nhỏ của (O;R) và (O’;R’) bằng nhau nên góc ở tâm của chúng bằng nhau

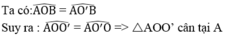
Suy ra : OA = O’A hay R = R’

a) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{2.6 + ( - 3).4}}{{\sqrt {{2^2} + {{\left( { - 3} \right)}^2}} .\sqrt {{6^2} + {4^2}} }} = 0 \Rightarrow \overrightarrow a  \bot \overrightarrow b \)

b) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{3.5 + 2.( - 1)}}{{\sqrt {{3^2} + {2^2}} .\sqrt {{5^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 45^\circ \)

c) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{\left( { - 2} \right).3 + ( - 2\sqrt 3 ).\sqrt 3 }}{{\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 2\sqrt 3 } \right)}^2}} .\sqrt {{3^2} + {{\sqrt 3 }^2}} }} =  - \frac{{\sqrt 3 }}{2} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 150^\circ \)

a) Khi a, b là hai số dương:

|a| = a; |b| = b

Khi đó, |a| < |b| , tức là a < b

Vậy a < b

b) Khi a, b là hai số âm:

|a| = - a; |b| = - b

Khi đó, |a| < |b| , tức là - a < - b hay a > b

Vậy a > b

a: |a|<|b|

mà a,b dương

nên a<b

b: a,b là hai số âm

|a|<|b|

Do đó: a>b

a) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}}  = \left( {1;3} \right),\overrightarrow {{n_2}}  = \left( {1; - 2} \right)\)

Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {1.1 + 3.( - 2)} \right|}}{{\sqrt {{1^2} + {3^2}} \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} \approx 0,93 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) \approx 22^\circ 8'\)

b) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}}  = \left( {4; - 2} \right),\overrightarrow {{n_2}}  = \left( {2; - 1} \right)\)

Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {4.2 + ( - 2).( - 1)} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = 1 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = 0^\circ \)

c) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\)lần lượt là \(\overrightarrow {{n_1}}  = \left( {2; - 1} \right),\overrightarrow {{n_2}}  = \left( {1;2} \right)\)

Ta có \({a_1}{a_2} + {b_1}{b_2} = 2.1 + ( - 1).2 = 0\)

Suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = 90^\circ \)

giúp mình với được ko ạh

giúp mình đi được ko, mình đang cần gấp

Bài 2: So sánh các phân số sau

7/15 > 5/13              11/12 > 7/48        24/35 > 21/7           15/26 > 7/8