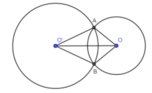
Vì số đo hai cung nhỏ của (O;R) và (O’;R’) bằng nhau nên góc ở tâm của chúng bằng nhau
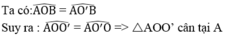
Suy ra : OA = O’A hay R = R’

Vì số đo hai cung nhỏ của (O;R) và (O’;R’) bằng nhau nên góc ở tâm của chúng bằng nhau
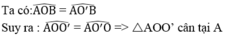
Suy ra : OA = O’A hay R = R’
Cho hai đường tròn (O; R) và (O’ ; R’) cắt nhau tại A ,B .Hãy so sánh R và R’ trong các trường hợp sau: Số đo cung nhỏ AB của (O ;R) nhỏ hơn số đo cung nhỏ AB của (O’ ;R’)
Cho hai đường tròn (O; R) và (O’ ; R’) cắt nhau tại A ,B .Hãy so sánh R và R’ trong các trường hợp sau: Số đo cung nhỏ AB của (O ;R) lớn hơn số đo cung nhỏ AB của (O’ ;R’)
cho hai đường tròn (O,R) và (O`,R )cắt nhau ở Avà B a, tứ giác AOBO` là hình j vì sao b, biết AB bằng R , tính số đo các cung nhỏ AB , cung lớn AB thuộc 2 đường tròn trên
Cho hai đường tròn (O;R) và (O’;R’) cắt nhau tại A,B.Đường phân giác cuả góc OBO’ cắt các đường tròn (O) , (O’) tương ứng tại C,D. Hãy so sánh các góc ở tâm BOC và BO’D
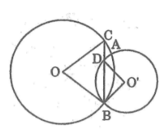
Hướng dẫn: Sử dụng các tam giác cân OBC ,O’BD
Cho hai đường tròn đồng tâm (O;R) và (O; ). Trên đường tròn nhỏ lấy một điểm M . Tiếp tuyến tại M của đường tròn nhỏ cắt đường tròn lớn tại A và B. Tia OM cắt đường tròn lớn tại C. a) Chứng minh rằng = ( cung CA bằng cung CB) b) Tính số đo của hai cung AB
Cho các đường tròn (O; R) và (O’; R’) tiếp xúc trong với nhau tại A (R > R’). Vẽ đường kính AB của (O), AB cắt (O’) tại điểm thứ hai C. Từ B vẽ tiếp tuyến BP với đường tròn (O’), BP cắt (O) tại Q. Đường thẳng AP cắt (O) tại điểm thứ hai R. Chứng minh:
a, AP là phân giác của B A Q ^
b, CP và BR song song với nhau
Cho đường tròn (O;R), 2 dây cung AB và CD cắt nhau tại điểm M nằm bên trong đường tròn.
a) Cm rằng nếu AB=CD thì MA=MC
b) Trường hợp AB>CD. Hãy so sánh khoảng cách từ M đến trung điểm của các dây AB, CD (vẽ hình luôn nha)
Cho đường tròn (O, r) đường kính Bc. Lấy dây AD = R, dây AC và BD cắt nhau tại E. Tìm số đo cung nhỏ AC