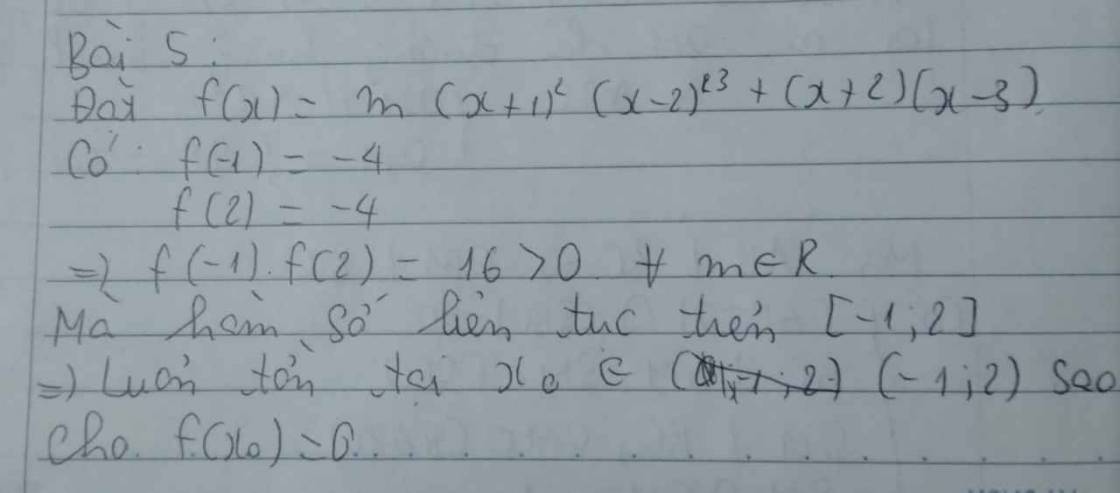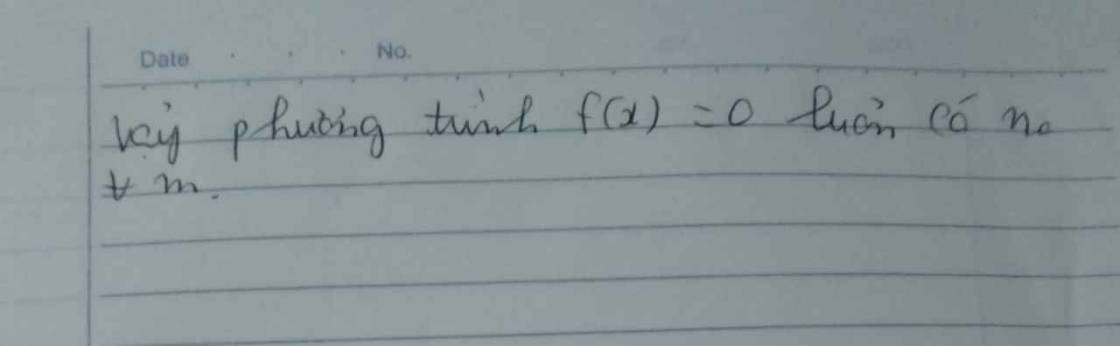Xét hàm \(f\left(x\right)=m\left(x-1\right)^3\left(x^2-4\right)+x^4-3\)

Hàm \(f\left(x\right)\) là hàm liên tục trên R

\(f\left(1\right)=-2< 0\)

\(f\left(-2\right)=13>0\)

\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)

\(f\left(2\right)=13>0\Rightarrow f\left(1\right).f\left(2\right)< 0\)

\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\)

\(\Rightarrow\) Phương trình đã cho luôn có ít nhất 2 nghiệm với mọi m

Đặt \(f\left(x\right)=x^4-\left(3m-2\right)x^3+mx-1\)

Hiển nhiên \(f\left(x\right)\) liên tục và xác định trên R

\(f\left(0\right)=-1< 0\)

\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\left(x^4-\left(3m-2\right)x^3+mx+1\right)=+\infty\) dương

\(\Rightarrow\) Luôn tồn tại 1 số thực \(a>0\) đủ lớn sao cho \(f\left(a\right)>0\)

\(\Rightarrow f\left(0\right).f\left(a\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;a\right)\) hay \(\left(0;+\infty\right)\)

\(\lim\limits_{x\rightarrow-\infty}\left(x^4-\left(3m-2\right)x^3+mx-1\right)=+\infty\) dương

\(\Rightarrow\) Luôn tồn tại 1 số thực \(b< 0\) sao cho \(f\left(b\right)>0\)

\(\Rightarrow f\left(0\right),f\left(b\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-\infty;0\right)\)

Vậy phương trình luôn có ít nhất 2 nghiệm với mọi m

Đặt \(f\left(x\right)=\left(1+m^2\right)\left(x-1\right)^3+x^2-2\)

\(f\left(x\right)\) là hàm đa thức nên liên tục trên R

\(f\left(1\right)=-1< 0\)

\(f\left(2\right)=1+m^2+4-2=m^2+3>0;\forall m\)

\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) với mọi m

Hay pt luôn có ít nhất 1 nghiệm dương với mọi m

Xét hàm số f(x)=m(x+1)2(x−2)3+(x+2)(x−3)f(x)=m(x+1)2(x−2)3+(x+2)(x−3) xác định và liên tục trên RR

⇒f(x)⇒f(x) xác định và liên tục trên [−2;3][−2;3].

Ta có: {f(−2)=−64mf(3)=16m⇒f(−2).f(3)=−1024m2{f(−2)=−64mf(3)=16m⇒f(−2).f(3)=−1024m2.

+ Với m=0⇒f(−2)=f(3)=0m=0⇒f(−2)=f(3)=0

⇒⇒ Phương trình f(x)=0f(x)=0 có nghiệm x=−2,x=−2, x=3.x=3.

+ Với m≠0⇒f(−2).f(3)<0m≠0⇒f(−2).f(3)<0

⇒⇒ Phương trình f(x)=0f(x)=0 có ít nhất một nghiệm thuộc (−2;3)(−2;3).

Vậy phương trình f(x)=0f(x)=0 luôn có nghiệm với mọi tham số m.

Xét hàm số \(f\left(x\right)=m\left(x+1\right)^2\left(x-2\right)^3+\left(x+2\right)\left(x-3\right)\)
f(x)=m(x+1)2(x−2)3+(x+2)(x−3), \(D=ℝ\)
R⇒f(x)⇒f(x) xác định và liên tục trên [−2;3][−2;3].

Ta có: \(\left\{{}\begin{matrix}f\left(-2\right)=-64m\\f\left(3\right)=16m\end{matrix}\right.\)
\(\Rightarrow f\left(-2\right).f\left(3\right)=-1024m^2\)

+ Với m=0⇒f(−2)=f(3)=0m=0⇒f(−2)=f(3)=0

⇒⇒ Phương trình f(x)=0f(x)=0 có nghiệm x=−2,x=−2, x=3.x=3.

+ Với m≠0⇒f(−2).f(3)<0m≠0⇒f(−2).f(3)<0

⇒⇒ Phương trình f(x)=0f(x)=0 có ít nhất một nghiệm thuộc (−2;3)(−2;3).

Vậy phương trình f(x)=0f(x)=0 luôn có nghiệm với mọi tham số m.