Cho parabol x^2 -4x -5 Cho A(1;3) B(4;-1), tìm C,D thuộc parabol sao cho ABCD là hình bình hành Mọi người giúp e với ạ

Những câu hỏi liên quan
Cho Parabol \(y=x^2\) . Tìm điểm A thuộc parabol sao cho tiếp tuyến với parabol tại A song song với đường thẳng y = 4x + 5
Gọi phương trình tiếp tuyến d tại A của parabol có dạng \(y=4x+b\) (\(b\ne5\))
Pt hoành độ giao điểm d và (P):
\(x^2=4x+b\Leftrightarrow x^2-4x-b=0\) (1)
d tiếp xúc (P) \(\Leftrightarrow\) (1) có nghiệm kép
\(\Leftrightarrow\Delta'=4+b=0\Rightarrow b=-4\)
Hoành độ giao điểm: \(x=\frac{4}{2.1}=2\Rightarrow y=4\Rightarrow A\left(2;4\right)\)
Đúng 0
Bình luận (0)
Cho đường thẳng y = x2. Tìm điểm A thuộc parabol sao cho tiếp tuyến với parabol tại A song song với đường thẳng y = 4x+5
Cho bất phương trình \({x^2} - 4x + 3 > 0\left( 2 \right)\).
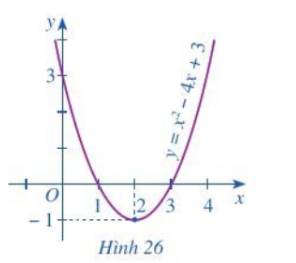
Quan sát parabol \(\left( P \right):{x^2} - 4x + 3\) ở Hình 26 và cho biết:
a) Bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía nào của trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với những giá trị nào của x.
a) Từ đồ thị ta thấy bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía trên trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với các giá trị của x thuộc \(\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
Đúng 0
Bình luận (0)
a. Giải phương trình $x^2 + x^4 - 6 = 0$.
b. Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng $d:$ $y = 4x + 1 - m$ và parabol $(P):$ $y = x^2$. Tìm giá trị của $m$ để $d$ cắt $(P)$ tại hai điểm phân biệt có tung độ $y_1$ và $y_2$ sao cho $\sqrt{y_1}.\sqrt{y_2} = 5.$
Bài 1 :
Đặt \(x^2=t\left(t\ge0\right)\)khi đó phương trình tương đương
\(t+t^2-6=0\)
Ta có : \(\Delta=1+24=25\)
\(t_1=\frac{-1-5}{2}=-3;t_2=\frac{-1+5}{2}=2\)
TH1 : \(x^2=-3\)( vô lí )
TH2 : \(x^2=2\Leftrightarrow x=\pm\sqrt{2}\)
Vậy tập nghiệm của phương trình là S = { \(\pm\sqrt{2}\)}
a) \(x^2+x^4-6=0\)
Đặt \(x^2=t\left(t\ge0\right)\)
⇒ t + \(t^2\) - 6 = 0
⇒ \(t^2+t-6=0\)
⇒ Δ = \(1^2-4.\left(-6\right)\)
= 25
x1 = \(\dfrac{-1-5}{2}\) = - 3 (L)
x2 = \(\dfrac{-1+5}{2}\) = 2 (TM)
Thay \(x^2\) = 2 ⇒ x = \(\pm\sqrt{2}\)
Vậy x = \(\left\{\sqrt{2};-\sqrt{2}\right\}\)
b) (d) : y = 4x +1 - m
(p) : y = \(x^2\)
Xét phương trình hoành độ giao điểm
\(x^2=4x+1-m\)
⇒ \(x^2-4x+m-1=0\)
Δ' = 4 - m + 1
= 5 - m
Để (d) cắt (p) tại hai điểm phân biệt thì Δ' > 0
5 - m > 0
⇒ m < 5
Vậy m < 5 thì (d) cắt (p) tại hai điểm phân biệt
Gọi tọa độ giao điểm của (d) và (p) là (x1;y1) và (x2;y2)
Theo Vi-ét : \(\left\{{}\begin{matrix}S=x_1+x_2=4\\P=x_1x_2=m-1\end{matrix}\right.\)
và y1 = \(x_1^{2_{ }}\) ; y2 = \(x_2^2\)
Khi đó : \(\sqrt{y_1}.\sqrt{y_2}=5\) ⇒ \(\sqrt{y_1.y_2}=5\)
⇔ \(\sqrt{\left(x_1x_2\right)^2}=5\) ⇔ \(|m-1|=5\)
⇔ \(\left[{}\begin{matrix}m-1=5\\m-1=-5\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}m=6\left(L\right)\\m=-4\left(TM\right)\end{matrix}\right.\)
Vậy m = - 4 thì TMĐKBT
a. Giải phương trình x^2 + x^4 - 6 = 0x
2
+x
4
−6=0.
b. Trong mặt phẳng tọa độ OxyOxy cho đường thẳng d:d: y = 4x + 1 - my=4x+1−m và parabol (P):(P): y = x^2y=x
2
. Tìm giá trị của mm để dd cắt (P)(P) tại hai điểm phân biệt có tung độ y_1y
1
và y_2y
2
sao cho \sqrt{y_1}.\sqrt{y_2} = 5.
y
1
.
y
2
=5.
Hướng dẫn giải:
a. Đặt x^2 = tx
2
=t, t \ge 0t≥0 thì phương trình đã cho trở thành:
t^2 + t - 6 = 0 \Leftrightarrow t^2 - 2t + 3t - 6 = 0 \Leftrightarrow (t-2)(t+3) = 0t
2
+t−6=0⇔t
2
−2t+3t−6=0⇔(t−2)(t+3)=0 \Leftrightarrow \left[\begin{aligned} & t = 2 \ \text{(thỏa mãn)} \\ & t = -3 \ \text{(loại)} \\ \end{aligned} \right.⇔[
t=2 (thỏa m
a
˜
n)
t=−3 (loại)
.
Với t = 2t=2 thì x^2 = 2 \Leftrightarrow x = \pm \sqrt 2.x
2
=2⇔x=±
2
.
Vậy phương trình có nghiệm x = \pm \sqrt2x=±
2
.
b. Phương trình hoành độ giao điểm: x^2 = 4x + 1 - mx
2
=4x+1−m \Leftrightarrow x^2 - 4x + m -1 = 0⇔x
2
−4x+m−1=0 (1)
\Delta' = 4 - m + 1 = 5 - mΔ
′
=4−m+1=5−m.
Để dd cắt (P)(P) tại hai điểm phân biệt thì phương trình (1) có 2 nghiệm phân biệt
\Leftrightarrow \Delta' > 0 \Leftrightarrow m < 5⇔Δ
′
>0⇔m<5.
Gọi hai giao điểm của dd và (P)(P) có tọa độ (x_1;y_1)(x
1
;y
1
) và (x_2;y_2)(x
2
;y
2
).
Ta có định lí Vi - et: \left\{\begin{aligned} & x_1 + x_2 = 4\\ & x_1x_2 = m-1 \end{aligned} \right.{
x
1
+x
2
=4
x
1
x
2
=m−1
và y_1 = x_1^2y
1
=x
1
2
; y_2 = x_2 ^2y
2
=x
2
2
.
Khi đó \sqrt{y_1}.\sqrt{y_2} = 5 \Leftrightarrow \sqrt{y_1.y_2} = 5
y
1
.
y
2
=5⇔
y
1
.y
2
=5
\Leftrightarrow \sqrt{(x_1x_2)^2} = 5 \Leftrightarrow |m-1| = 5⇔
(x
1
x
2
)
2
=5⇔∣m−1∣=5
\Leftrightarrow \left[\begin{aligned} & m - 1 = 5\\ & m - 1 = -5 \end{aligned} \right. \Leftrightarrow \left[\begin{aligned} & m = 6 \ \text{(loại)} \\ & m = -4 \ \text{(thỏa mãn)} \end{aligned} \right.⇔[
m−1=5
m−1=−5
⇔[
m=6 (loại)
m=−4 (thỏa m
a
˜
n)
.
Vậy với m = -4m=−4 thì dd cắt (P)(P) tại hai điểm phân biệt có tung độ y_1y
1
và y_2y
2
sao cho \sqrt{y_1}.\sqrt{y_2} = 5.
y
1
.
y
2
=5.
Xem thêm câu trả lời
Tìm parabol y =a^2 - 4x+c biết rằng parabol đi qua điểm A (1;-1) và có trục đối xứng x = 2
a ) Tìm tọa độ giao điểm của đường thẳng d : y = - x + 2 và Parabol : y = x2
b ) Cho hệ phương trình : \(\left\{{}\begin{matrix}4x+ay=b\\x-by=a\end{matrix}\right.\) . Tìm a và b để hệ đã cho có nghiệm duy nhất ( x , y ) = ( 2 : -1 )
a. Theo bài ra ta có: \(x^2+x-2=0\)
\(\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=-\left(-2\right)+2=4\\y=-1+2=1\end{matrix}\right.\)
Vậy tọa độ giao điểm cần tìm là: \(\left(-2;4\right)\); \(\left(1:1\right)\)
b. Thay x = 2 ; y = -1 vào hpt ta có:
\(\left\{{}\begin{matrix}8-a=b\\2+b=a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-a-b=-8\\-a+b=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=5\\b=3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy, cho parabol (P) : x2 - 4x + 9. Hỏi parabol nào sau đây là ảnh của parabol (P) qua phép đối xứng trục, có trục là đường thẳng x - 2 = 0
Parabol \(y=x^2-4x+9\) có trục đối xứng là đường thẳng \(x=-\dfrac{b}{2a}=2\)
Nên phép đối xứng trục qua đường thẳng \(x-2=0\) hay \(x=2\) sẽ cho ảnh là chính nó
Hay pt ảnh của (P) vẫn là \(x^2-4x+9\)
Đúng 1
Bình luận (0)
Cho parabol (P): \(y=2x^2+6x-1\)
Tìm giá trị của k để đường thẳng Δ: \(y=x\left(k+6\right)+1\) cắt parabol tại hai điểm phân biệt M,N sao cho trung điểm của đoạn thẳng MN nằm trên đường thẳng d: \(4x+2y-3=0\)
Cho parabol P : y= -x^2 + 4 x+5
a Khảo sát và vẽ đồ thị của hàm số P
b Dựa vào đồ thị P hãy biện luận số nghiệm phương trình x^2-4x-5-m

















