Tung vòng và chạy theo đường tạo thành hình tứ giác.
Cắt miếng bìa hình tam giác đều cạnh bằng 1 như hình bên và gấp theo các đường kẻ, sau đó dán các mép lại để được hình tứ diện đều. Tính thể tích V của hình tứ diện tạo thành.

A. V = 2 96
B. V = 3 16
C. V = 3 32
D. V = 2 12
Trên mặt phẳng tọa độ Oxy xét tam giác vuông OAB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA+OB=1 Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác OAB quanh trục Oy bằng bao nhiêu?
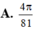
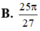
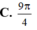
![]()
Trên mặt phẳng tọa độ Oxy, xét tam giác vuông AOB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA + OB = 1. Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác AOB quanh trục Oy bằng bao nhiêu?
A. 4 π 81
B. 15 π 27
C. 9 π 4
D. 17 π 9
Trên mặt phẳng tọa độ Oxy, xét tam giác vuông OAB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA + OB = 1. Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác OAB quanh trục Oy bằng bao nhiêu?
A. 4 π 81
B. 25 π 27
C. 9 π 4
D. 17 π 9
Đáp án A
Khi quay ∆ O A B quanh trục Oy, ta được hình nón có bán kính đáy r = OA và chiều cao h = OB. Theo bài ra, ta có OA + OB = r + h = 1 với (0 < r, h < 1)
Khi đó, thể tích khối nón là V N = 1 3 πr 2 h = 1 3 πr 2 1 - r .
Ta có r 2 1 - r 2 = 4 . r 2 . r 2 . 1 - r ≤ 4 . r 2 + r 2 + 1 - r 3 27 = 4 27 ⇒ V N ≤ 1 3 π . 4 27 = 4 π 81 .
Tham khảo: Ta có thể đưa điểm B có tung độ âm về tung độ dương thì thể tích của khối nón không đổi.
Gọi A a ; 0 B 0 ; b a , b > 0 suy ra phương trình đường thẳng A B : x y + y b = 1 ⇒ x = a - a b . y .
Khi đó V O y = π . ∫ a b a - a b y 2 d y = πa 2 b 3 .
Ta có 4 π 3 . a 2 . a 2 . b ≤ 4 π 3 . a 2 + a 2 + b 3 27 = 4 π 81 ⇒ V M a x = 4 π 81 .
Cô giáo phát cho mỗi bạn một sợi dây. Cô đề nghị cả lớp dùng sợi dây đó để xếp thành hình tam giác hoặc hình tứ giác theo ý thích, sau đó đo độ dài các cạnh và tính chu vi của hình mà mình tạo được. Cô đi một vòng quanh lớp và nhận xét: “ Mỗi bạn trong lớp tạo được một hình khác nhau vậy mà cả lớp lại chung một kết quả. Thật là kì diệu.” Biết rằng lời của cô giáo là hoàn toàn chính xác, em hãy giải thích tại sao.
Vì chu vi của một hình là tổng độ dài các đoạn thẳng bao quanh của hình đó.
Nên khi dùng một sợi dây để tạo thành một hình tam giác hoặc tứ giác bất kì thì chu vi của các hình đó đều bằng độ dài sợi dây đã cho.
Cho nửa đường tròn tâm O đường kính AB = 2a. Trên nửa đường tròn (O) xác định các điểm M và K sao cho K nằm trên cung AM và góc KOM = 90o. Gọi Q là giao điểm của BK với AM và P là giao điểm của AK với BM.
a. CMR MQKP là tứ giác nội tiếp
b. CMR tam giác AMP là tam giác vuông cân
c. Tính diện tích hình quạt tròn KOM ứng với cung nhỏ KM theo a.
d. Quay tam giác KOM một vòng quanh cạnh OK. Tính diện tích xung quanh và thể tích của hình tạo thành khi a = \(3\sqrt{2}\)cm
Một công viên có hai đường chạy bộ hình tam giác đồng dạng như Hình 15. Kích thước của con đường bên trong lần lượt là 300 m, 350 m và 550 m. Cạnh ngắn nhất của con đường bên ngoài là 600 m. Nam chạy bốn vòng bên trong. Hưng chạy hai vòng bên ngoài. So sánh quãng đường chạy của hai bạn.

Quan sát hình vẽ ta thấy, cạnh ngắn nhất của tam giác \(ABC\) là cạnh \(AC\);cạnh ngắn nhất của tam giác \(DEF\) là cạnh \(DF\).
Do đó, ta có: \(\frac{{AC}}{{DF}} = \frac{{600}}{{300}} = 2\).
Do đó, tỉ số chu vi của tam giác \(ABC\) và tam giác \(DEF\) là 2.
Chu vi tam giác \(DEF\) là: \(300 + 350 + 550 = 1200m\)
Chu vi tam giác \(ABC\) là: \(1200.2 = 2400m\).
Quãng đường bạn Nam đã chạy là: \(1200.4 = 4800m\)
Quãng đường bạn Hùng đã chạy là: \(2400.2 = 4800m\).
Do đó, hai bạn Nam và Hùng đã chạy hai quãng đường bằng nhau.
Cho tứ giác ABCD có các đường phân giác trong tạo thành 1 tứ giác.Chứng minh tứ giác đó có các góc đối bù nhau(Giải theo cách lớp 8 giúp mình)
![[IMG]](http://i.imgur.com/S6gY3so.png)
Tất cả giao điểm được thể hiện trên hình ( vẽ hơi xấu ![]() )
)
Xét ΔADQΔADQ có: MQPˆ=DAQˆ+ADQˆMQP^=DAQ^+ADQ^ (góc ngoài tam giác)
Xét ΔBCNΔBCN có : MNPˆ=BCNˆ+CBNˆMNP^=BCN^+CBN^
⟹MQPˆ+MNPˆ=DAQˆ+ADQˆ+BCNˆ+CBNˆ=1/2(ABCˆ+BCDˆ+CADˆ+DABˆ)=1/2.360o=180o
Em tham khảo tại link dưới đây nhé:
Câu hỏi của Hoàng Tử Bóng Đêm Kiyoshi - Toán lớp 8 - Học toán với OnlineMath
Cho tam giác ABC , đường cao AH . Gọi M là trung điểm của cạnh BC . Qua M kẻ các đường thẳng song song với AB và AC , chúng cắt các cạnh AC và AB theo thứ tự tại E và D .
a) Cmr : Tứ giác ADME là hình bình hành . Gọi O là giao điểm của AM và DE . Cmr : Tam giác OAH cân .
b) Tứ giác tạo thành từ 4 điểm D , E , M , H là hình gì ? Tại sao ?
c) Tìm điều kiện của tam giác ABC để tứ giác ADME là hình chữ nhật .
Trong trường hợp này hãy xác định vị trí của điểm M trên cạnh BC để độ dài đoạn thẳng DE nhỏ nhất
1) ADME là h.b.h (vì có 2 cặp cạnh đối song song)
2) Vì ADME là hình chữ nhật nên O là trung điểm 2 đường chéo AM và DE.
Xét tam giác AHM vuông tại H, đường trung tuyến HO, khi đó HO = AO = OM
Vậy tam giác AHO cân ở O
3)
a, Tam giác ABC vuông tại A nên ˆDAE=900DAE^=900
Mà ADME là h.b.h nên tứ giác ADME là hình chữ nhật
b, Vì tứ giác AEMD là hình chữ nhật nên ED=AM
Để DE có độ dài nhỏ nhất thì AM có độ dài nhỏ nhất hay M là chân đường vuông góc hạ từ A xuống BC