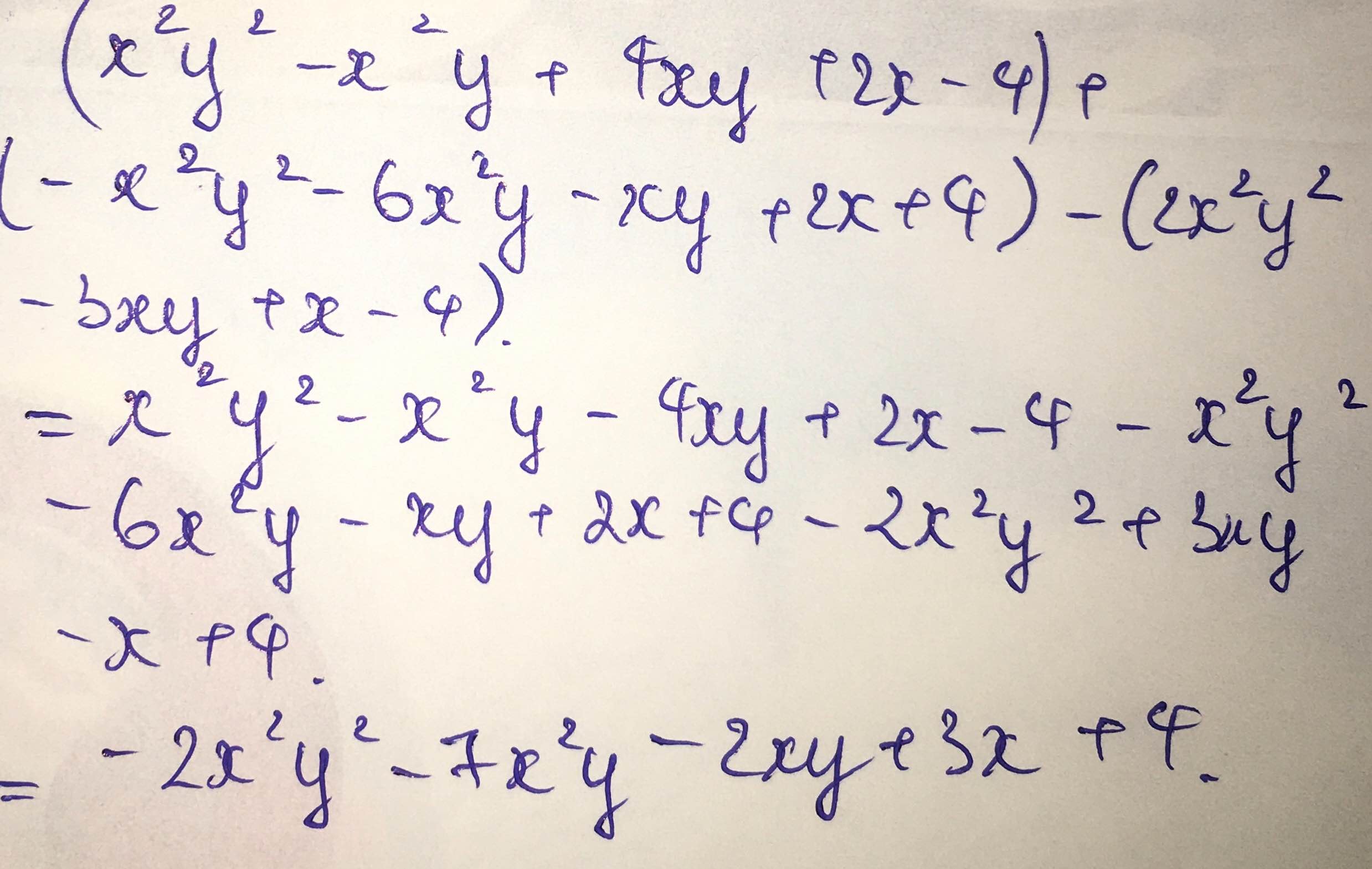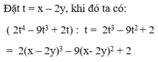(x+2y)(x-2y)

Những câu hỏi liên quan
Chứng minh đẳng thức:
(\(\dfrac{x}{x+2y}\) - \(\dfrac{x+2y}{2y}\))(\(\dfrac{x}{x-2y}\) - 1 + \(\dfrac{8y^3}{8y^3-x^3}\) ) = \(\dfrac{x}{2y-x}\)
\(\left(\dfrac{x}{x+2y}-\dfrac{x+2y}{2y}\right)\left(\dfrac{x}{x-2y}-1+\dfrac{8y^3}{8y^3-x^3}\right)=\dfrac{2xy-\left(x+2y\right)^2}{2y\left(x+2y\right)}\left(\dfrac{2y}{x-2y}+\dfrac{8y^3}{\left(2y-x\right)\left(4y^2+2yx+x^2\right)}\right)=\dfrac{-\left(x^2+2xy+4y^2\right)}{2y\left(x+2y\right)}\cdot\dfrac{2y\left(4y^2+2yx+x^2\right)-8y^3}{\left(x-2y\right)\left(x^2+2xy+4y^2\right)}=\dfrac{-\left(x^2+2xy+4y^2\right)2y\left(4y^2+2xy+x^2-4y^2\right)}{2y\left(x+2y\right)\left(x-2y\right)\left(x^2+2x+4y^2\right)}=\dfrac{-\left(x^2+2xy\right)}{\left(x+2y\right)\left(x-2y\right)}=\dfrac{x}{2y-x}\)
Đúng 0
Bình luận (0)
(x^2y^2 - x^2y + 4xy + 2x - 4) + (-x^2y^2 - 6x^2y - xy + 2x+4) - (2x^2y^2 - 3xy +x - 4)
=
Câu: Đẳng thức nào sau đây là đúng. *
4x^3y^2 – 8x^2y^3 = 4x^2.y(xy – 2y^2)
4x^3y^2 – 8x^2y^3 = 4x^2y^2(x – 2y)
4x^3y^2 – 8x^2y^3 = x^2y^2(x – 2y)
4x^3y^2 – 8x^2y^3 = 4x^2y^2(x – y)
ta có 4 x 3 y 2 – 8 x 2 y 3 = 4 x 2 y 2 . x – 4 x 2 y 2 . 2 y = 4 x 2 y 2 ( x – 2 y )
Vậy 4x3y2 – 8x2y3 = 4x2y2(x – 2y)
Đáp án cần chọn là: C
bấm đúng cho mik đi
Đúng 3
Bình luận (0)
Câu 13: Đa thức x2 – 6x –4y2 + 9 được phân tích thành nhân tử có kết quả là
A. (x + 2y + 3)(x + 2y - 3)
B. (x – 3 – 2y)(x – 3 + 2y)
C. (x – 2y - 3)(x - 2y + 3)
D. (x – 3 – 4y)(x – 3 + 4y)
(x+y/2x-2y-x-y/2x+2y-2y^2/y^2-x^2):2y/x-y
Ta có: \(\left(\dfrac{x+y}{2x-2y}-\dfrac{x-y}{2x+2y}-\dfrac{2y^2}{y^2-x^2}\right):\dfrac{2y}{x-y}\)
\(=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2+4y^2}{2\left(x-y\right)\left(x+y\right)}:\dfrac{2y}{x-y}\)
\(=\dfrac{4y^2+4xy}{2\left(x-y\right)\left(x+y\right)}\cdot\dfrac{x-y}{2y}\)
\(=\dfrac{4y\left(x+y\right)}{2\left(x+y\right)\cdot2y}\)
\(=1\)
Đúng 0
Bình luận (0)
Tính GTBT. a, xy*(x+y)-2x-2y tại x+y=10. . x*y=12 . b, x^5(x+2y)-x^3y*(x+2y)+x^2y^2*x+2y. Tại x=10. . y=5
, xy*(x+y)-2x-2y tại x+y=10
->10xy-2(x+y)=10xy-20=120-20=80
b, x^5(x+2y)-x^3y*(x+2y)+x^2y^2*x+2y=(x+2y)(x^5-x^3y+x^2y^2)
Bạn tự thay vảo nhá
Đúng 0
Bình luận (0)
tính tổng S = x + 2y + 3z biết rằng 1/(x+ 2y) + 1/(2y+3z)+1/(x+3z)= 12x/(2y+3z)+24y/(x+3z)+ 36z/(x+2y)=2016
\(\left\{{}\begin{matrix}\frac{1-x+2y}{x-2y}+x+2y=4\\\frac{x+2y}{x-2y}-6=0\end{matrix}\right.\)
ĐKXĐ: \(x\ne2y\)
Biến đổi pt dưới:
\(x+2y-6\left(x-2y\right)=0\)
\(\Rightarrow5x=14y\Rightarrow x=\frac{14y}{5}\)
Thay vào pt trên:
\(\frac{1-\frac{14}{5}y+2y}{\frac{14}{5}y-2y}+\frac{14}{5}y+2y=4\)
\(\Leftrightarrow\frac{5}{4y}+\frac{24}{5}y-5=0\)
\(\Leftrightarrow\frac{24}{5}y^2-5y+\frac{5}{4}=0\) \(\Rightarrow\left[{}\begin{matrix}y=\frac{5}{12}\\y=\frac{5}{8}\end{matrix}\right.\) \(\Rightarrow x=\frac{14}{5}y=...\)
Đúng 0
Bình luận (0)
Thưc hiện phép tính chia:
2
(
x
-
2
y
)
4
-
9
(
x
-
2
y
)
3
+
2
(
x
-
2
y
)...
Đọc tiếp
Thưc hiện phép tính chia: 2 ( x - 2 y ) 4 - 9 ( x - 2 y ) 3 + 2 ( x - 2 y ) : ( x - 2 y )
A. 2 ( x - 2 y ) 2 - 9 ( x - 2 y ) + 2
B. ( x - 2 y ) 3 - ( x - 2 y ) 2 + 2
C. 2 ( x - 2 y ) 3 - 9 ( x - 2 y ) 2 + 2
D. 2 ( x - 2 y ) 3 + 2
tìm đa thức m biết
3x^2y^3 - x^2y - M=x^2y^3 + x^2y
\(3x^2y^3-x^2y-M=x^2y^3+x^2y\\ \Rightarrow M=3x^2y^3-x^2y-x^2y^3-x^2y\\ \Rightarrow M=2x^2y^3-2x^2y\)
Đúng 1
Bình luận (0)
\(\Leftrightarrow M=3x^2y^3-x^2y-x^2y^3-x^2y=2x^2y^3-2x^2y\)
Đúng 1
Bình luận (0)