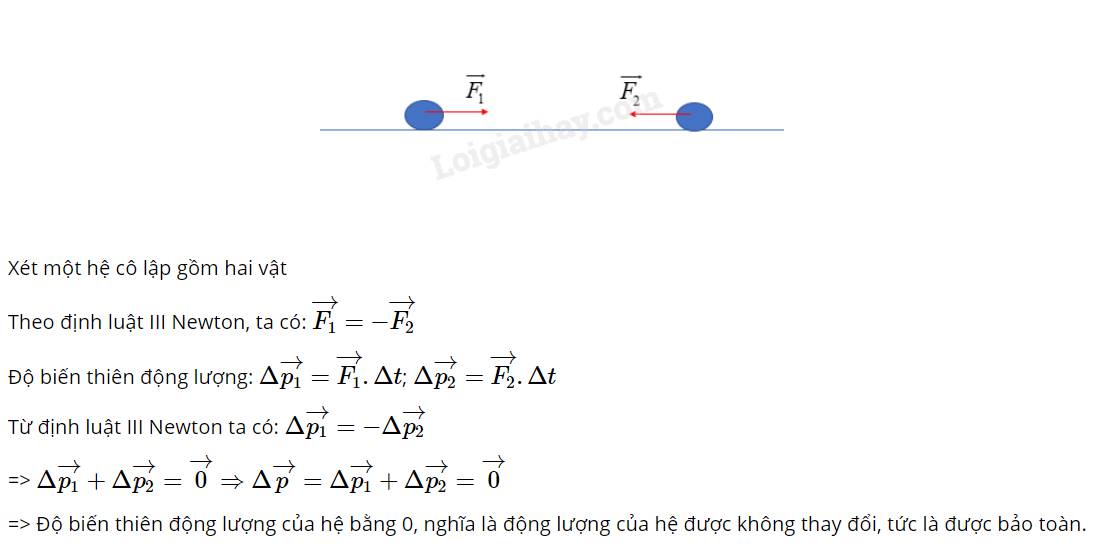
Lập luận để chứng tỏ tổng động lượng của hệ hai vật va chạm với nhau được bảo toàn.

Những câu hỏi liên quan
4. Lập luận để chứng tỏ tổng động lượng của hệ hai vật va chạm với nhau được bảo toàn.
Làm thế nào để xác định được lực tương tác giữa hai vật khi va chạm nếu không biết được động lượng của các vật trước và sau tương tác. Trong quá trình va chạm (Hình 19.1), động lượng và động năng của hệ có được bảo toàn hay không? Ngoài ra, những kiến thức về động lượng có thể được vận dụng trong thực tiễn như thế nào?
Đọc tiếp
Làm thế nào để xác định được lực tương tác giữa hai vật khi va chạm nếu không biết được động lượng của các vật trước và sau tương tác. Trong quá trình va chạm (Hình 19.1), động lượng và động năng của hệ có được bảo toàn hay không? Ngoài ra, những kiến thức về động lượng có thể được vận dụng trong thực tiễn như thế nào?

- Trong quá trình va chạm động lượng và động năng của hệ có được bảo toàn.
- Ngoài ra, những kiến thức về động lượng có thể được vận dụng trong thực tiễn như:
+ Hệ thống túi khí và đai an toàn trong ô tô giúp người ngồi trong xe hạn chế tối đa chấn thương khi xảy ra va chạm giao thông.
+ Vận động viên nhảy xa nhún chân, chùng đầu gối khi tiếp đất mục đích để tăng thời gian va chạm, giảm lực tác dụng.
+ Chế tạo hệ thống động cơ chuyển động bằng phản lực.
…
Đúng 0
Bình luận (0)
Chứng tỏ rằng trong hiện tượng va chạm mềm, động năng của hệ không bảo toàn.
Xét hệ hai vật có khối lượng m1, m2 chuyển động với vận tốc v1, v2 đến va chạm mềm với nhau. Vận tốc sau va chạm là v.
Động năng của hệ trước va chạm: W đ I = m 1 v 1 2 2 + m 2 v 2 2 2
Theo định luật bảo toàn động lượng, vận tốc của các vật ngay sau va chạm là:
v = m 1 v 1 + m 2 v 2 m 1 + m 2
Động năng của hệ sau va chạm:
W đ I I = ( m 1 + m 2 ) v 2 2 = 1 2 m 1 v 1 + m 2 v 2 2 m 1 + m 2
Độ biến thiên động năng của hệ:
Δ W đ = W đ I I − W đ I = 1 2 m 1 v 1 + m 2 v 2 2 m 1 + m 2 − m 1 v 1 2 2 − m 2 v 2 2 2
Δ W đ = − 1 2 m 1 m 2 m 1 + m 2 ( v 1 − v 2 ) 2 < 0
Điều này chứng tỏ trong va chạm mềm giưa hai vật, động năng không bảo toàn.
Đúng 0
Bình luận (0)
Một vật có khối lượng m1 chuyển động với vận tốc véctơ v0 Đến và chạm tâm với vật khối lượng m2 = m1/4 Đang nằm yên. Sau và chạm cả hai vật dính vào nhau và cùng chuyển động với vận tốc véctơ v. Tỉ số tổng động năng của hệ trước và sau va chạm là A. 1,25 B. 1,5 C. 0,8 D. 0.25
Một quả cầu A khối lượng 2 kg chuyển động trên máng thẳng ngang không ma sát với vận tốc 3 m/s và tới va chạm vào quả cầu B khối lượng 3 kg đang chuyển động với vận tốc 1 m/s cùngchiều với quả cầu A trên cùng một máng ngang. Xác định độ lớn của vận tốc và chiều chuyển động của hai quả cầu sau khi va chạm. Cho biết sự va chạm giữa hai quả cầu A và B có tính chất hoàn toàn đàn hồi, tức là sau khi va chạm thì các quả cầu này chuyển động tách rời khỏi nhau, đồng thời tổng động năng của chúng trước v...
Đọc tiếp
Một quả cầu A khối lượng 2 kg chuyển động trên máng thẳng ngang không ma sát với vận tốc 3 m/s và tới va chạm vào quả cầu B khối lượng 3 kg đang chuyển động với vận tốc 1 m/s cùng'chiều với quả cầu A trên cùng một máng ngang. Xác định độ lớn của vận tốc và chiều chuyển động của hai quả cầu sau khi va chạm. Cho biết sự va chạm giữa hai quả cầu A và B có tính chất hoàn toàn đàn hồi, tức là sau khi va chạm thì các quả cầu này chuyển động tách rời khỏi nhau, đồng thời tổng động năng của chúng trước và sau va chạm được bảo toàn (không thay đổi).
Chọn chiều chuyển động ban đầu của quả cầu A là chiều dương. Hệ vật gồm hai quả cầu A và B. Gọi v 1 , v 2 và v ' 1 , v ' 2 là vận tốc của hai quả cầu trước và sau khi va chạm.
Vì hệ vật chuyển động không ma sát và ngoại lực tác dụng lên hệ vật (gồm trọng lực và phản lực của máng ngang) đều cân bằng nhau theo phương thẳng đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn (viết theo trị đại số):
m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
2. v ' 1 + 3. v ' 2 = 2.3 +3.1 = 9
Hay v ' 1 + 1,5. v ' 2 = 4,5 ⇒ v ' 2 = 3 - 2 v ' 1 /3 (1)
Đồng thời, tổng động năng của hệ vật cũng bảo toàn, nên ta có:
m1 v ' 1 2 /2 + m2 v ' 2 2 /2 = m1 v 1 2 /2 + m2 v 2 2 /2
2 v ' 1 2 /2 + 3 v ' 2 2 /2 = 2. 3 2 /2 + 3. 1 2 /2
Hay v ' 1 2 + 1,5 v ' 2 2 = 10,5 ⇒ v ' 2 2 = 7 - 2 v ' 1 2 /3 (2)
Giải hệ phương trình (1), (2), ta tìm được: v ' 1 = 0,6 m/s; v ' 2 = 2,6 m/s
(Chú ý: Loại bỏ cặp nghiệm v ' 1 = 3 m/s, v ' 2 = 1 m/s, vì không thỏa mãn điều kiện v ' 2 > v 2 = 1 m/s)
Đúng 0
Bình luận (0)
Một vật khối lượng m đang chuyển động theo phương ngang với vận tốc v thì va chạm vào vật khối lượng 2m đang đứng yên. Sau va chạm, hai vật dính vào nhau và chuyển động với cùng vận tốc. Bỏ qua ma sát, vận tốc của hệ sau va chạm là A.
v
3
B.
v
C.
3
v
D.
v
2
Đọc tiếp
Một vật khối lượng m đang chuyển động theo phương ngang với vận tốc v thì va chạm vào vật khối lượng 2m đang đứng yên. Sau va chạm, hai vật dính vào nhau và chuyển động với cùng vận tốc. Bỏ qua ma sát, vận tốc của hệ sau va chạm là
A. v 3
B. v
C. 3 v
D. v 2
Chọn đáp án A
Áp dụng định luật bảo toàn động lượng: m v = ( m + 2 m ) V ⇒ V = v 3
Chú ý: Va cham ở bài toán trên là va chạm mềm
Đúng 0
Bình luận (0)
Lập luận để giải thích tại sao hệ hai xe trượt trong thí nghiệm khảo sát định luật bảo toàn động lượng được xem gần đúng là hệ kín.

Trước khi thực hiện thí nghiệm thì đệm khí được khởi động nên khi hai xe di chuyển va chạm vào nhau, sẽ không có lực ma sát cản trở chuyển động, chỉ còn tương tác giữa các vật trong hệ nên thí nghiệm được xem như gần đúng là hệ kín.
Đúng 0
Bình luận (0)
4. Lập luận để giải thích tại sao hệ hai xe trượt trong thí nghiệm khảo sát định luật bảo toàn động lượng được xem gần đúng là hệ kín.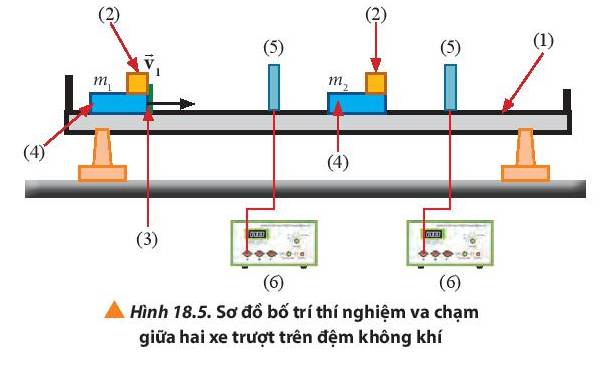
Trước khi thực hiện thí nghiệm thì đệm khí được khởi động nên khi hai xe di chuyển va chạm vào nhau, sẽ không có lực ma sát cản trở chuyển động, chỉ còn tương tác giữa các vật trong hệ nên thí nghiệm được xem như gần đúng là hệ kín.
Đúng 0
Bình luận (0)
Viên bi A có khối lượng 300g chuyển động trên mặt bàn nằm ngang với vận tốc 5m/s va chạm trực diện với viên bi B có khối lượng 100g đang đứng yên. Biết va chạm là hoàn toàn đàn hồi(động năng của hệ bảo toàn). Tính vận tốc của mỗi viên bi ngay sau va chạm
Bảo toàn động lượng ta có:
\(m_1v_1+m_2v_2=5m_1\)
\(\Leftrightarrow0,3v_1+0,1v_2=1,5\)
\(\Leftrightarrow3v_1+v_2=15\left(1\right)\)
Bảo toàn động năng lượng ta có:
\(\dfrac{1}{2}m_1v^2_1+\dfrac{1}{2}m_2v^2_2=\dfrac{25}{2}m_1\)
\(\Leftrightarrow3v^2_1+v_2^2=75\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3v_1+v_2=15\\3v_1^2+v^2_2=75\end{matrix}\right.\)
Giải hệ phương trình ta được:
\(\left\{{}\begin{matrix}v_1=2,5m/s\\v_2=7,5m/s\end{matrix}\right.\)
Đúng 2
Bình luận (1)