Những câu hỏi liên quan
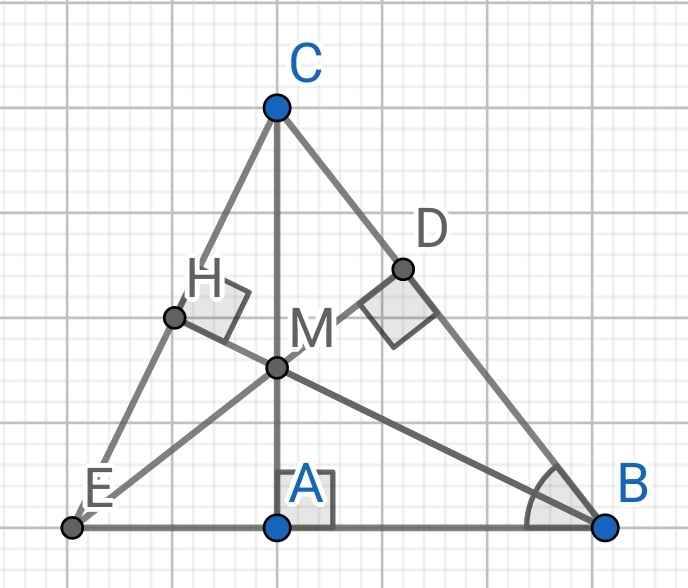
Cho tam. giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ MD BC (D BC).
a) Chứng minh BA = BD.
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh ABC = DBE.
c) Kẻ DH MC (H MC) và AK ME (K ME). Gọi N là giao điểm của hai tia DH và AK.
a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó:ΔBAM=ΔBDM
Suy ra:BA=BD
b: Xét ΔBDE vuông tại D và ΔBAC vuông tại A có
BD=BA
\(\widehat{DBE}\) chung
Do đó: ΔBDE=ΔBAC
Đúng 1
Bình luận (0)
Cho △ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ MD ⊥ BC (D ∈ BC).
a) Chứng minh BA = BD.
b) Gọi E là giao điểm của 2 đường thẳng DM và BA. Chứng minh △ABC = △DBE.
c) Chứng minh ME = MC.
d) Kẻ BH ⊥ EC tại H. Chứng minh 3 điểm B, M, H thẳng hàng.
 a) Do BM là tia phân giác của ABC (gt)
a) Do BM là tia phân giác của ABC (gt)
⇒ ∠ABM = ∠DBM
Xét hai tam giác vuông: ∆ABM và ∆DBM có:
BM là cạnh chung
∠ABM = ∠DBM (cmt)
⇒ ∆ABM = ∆DBM (cạnh huyền - góc nhọn)
⇒ BA = BD (hai cạnh tương ứng)
b) Xét hai tam giác vuông: ∆ABC và ∆DBE có:
BA = BD (cmt)
∠B chung
⇒ ∆ABC = ∆DBE (cạnh huyền - góc nhọn)
c) Do ∠ABM = ∠DBM (cmt)
⇒ ∠EBM = ∠CBM
Do ∆ABC = ∆DBE (cmt)
⇒ BC = BE (hai cạnh tương ứng)
Xét ∆MBE và ∆MBC có:
BE = BC (cmt)
∠EBM = ∠CBM (cmt)
BM là cạnh chung
⇒ ∆MBE = ∆MBC (c-g-c)
⇒ ME = MC (hai cạnh tương ứng)
c) ∆BCE có:
CA ⊥ AB (ABC vuông tại A)
⇒ CA ⊥ BE
⇒ CA là đường cao của ∆BCE (1)
MD ⊥ BC (gt)
⇒ ED ⊥ BC
⇒ ED là đường cao thứ hai của ∆BCE (2)
M là giao điểm của AC và ED
⇒ M là giao điểm của ba đường cao của ∆BCE
Mà BH ⊥ CE (gt)
⇒ BH là đường cao thứ ba của ∆BCE
⇒ B, M, H thẳng hàng
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ
M
D
⊥
B
C
(
D
∈
B
C
)
.
a) Chứng minh BA BD.b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh
∆
A
B
C
∆
D
B
E
.
c) Kẻ
D
H
⊥
M
C
(
H
∈
M
C...
Đọc tiếp
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ M D ⊥ B C ( D ∈ B C ) .
a) Chứng minh BA = BD.
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh ∆ A B C = ∆ D B E .
c) Kẻ D H ⊥ M C ( H ∈ M C ) và A K ⊥ M E ( K ∈ M E ) . Gọi N là giao điểm của hai tia DH và AK. Chứng minh MN là tia phân giác góc HMK.
d) Chứng minh ba điểm B, M, N thẳng hàng.
cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC ở M. Kẻ MD vuông góc BC
a)C/M BA=BD
b)Gọi E là giao điểm của DM và BA. C/M tâm giác ABC =tam giác DBE
c)Kẻ DH vuông góc MC (H vuông góc MC) và AK vuông góc ME (K vuông góc ME). Gọi N là giao điểm của DH và AK. C/M MN là tia phân giác góc HMK.
d)C/M B,M,N thẳng hàng.
a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó: ΔBAM=ΔBDM
=>BA=BD và MA=MD
b: Xét ΔBDE vuông tại D và ΔBAC vuông tại A có
BD=BA
\(\widehat{DBE}\) chung
Do đó: ΔBDE=ΔBAC
c: Xét ΔMKA vuông tại K và ΔMHD vuông tại H có
MA=MD
\(\widehat{KMA}=\widehat{HMD}\)
Do đó: ΔMKA=ΔMHD
=>MK=MH và AK=HD
Xét ΔNKM vuông tại K và ΔNHM vuông tại H có
NM chung
MK=MH
Do đó: ΔNKM=ΔNHM
=>NK=NH và \(\widehat{KMN}=\widehat{HMN}\)
=>MN là phân giác của góc HMK
d: NK+KA=NA
NH+HD=ND
mà NK=NH và KA=HD
nên NA=ND
=>N nằm trên đường trung trực của AD(1)
MA=MD
=>M nằm trên đường trung trực của AD(2)
BA=BD
=>B nằm trên đường trung trực của AD(3)
Từ (1),(2),(3) suy ra B,M,N thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M, vẽ MD vuông góc với BC tại D. a) Chứng minh BA = BD b) Gọi E là giao điểm của hai đường thẳng AB và DM. Chứng minh ∆ABC = ∆DBE.
a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
góc ABM=góc DBM
Do đó: ΔBAM=ΔBDM
=>BA=BD
b: XétΔABC vuông tại A và ΔDBE vuông tại D có
BA=BD
góc ABC chung
Do đo: ΔABC=ΔDBE
Đúng 0
Bình luận (1)
a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
góc ABM=góc DBM (BM là tia phân giác của góc B)
góc D= góc A=90độ
Do đó: ΔBAM=ΔBDM( cạnh huyền - góc nhọn )
=>BA=BD (2 cạnh tương ứng)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,tia phân giác góc B cắt cạnh AC tại M.Kẻ MD vuông góc với BC tại D.a)Chứng minh: góc BMA góc BMDb)Gọi E là giao điểm của hai đường thẳng MD và BA Chứng minh:ACDEc)Chứng minh: Δ A M E Δ D M Cd)Kẻ DH ⊥ MC tại H và AK ⊥ ME tại K.Hai tia DH và AK cắt nhau tại N.Chứng minh:MN là phân giác của góc KMHe)Chứng minh:Ba điểm B,M,N thẳng hàng g)Chứng minh:BN ⊥ AD,BN ⊥ ECh) Δ ABC thỏa mãn điều kiện gì để Δ NAD là tam giác đều
Đọc tiếp
Cho tam giác ABC vuông tại A,tia phân giác góc B cắt cạnh AC tại M.Kẻ MD vuông góc với BC tại D.
a)Chứng minh: góc BMA = góc BMD
b)Gọi E là giao điểm của hai đường thẳng MD và BA Chứng minh:AC=DE
c)Chứng minh: Δ A M E = Δ D M C
d)Kẻ DH ⊥ MC tại H và AK ⊥ ME tại K.Hai tia DH và AK cắt nhau tại N.Chứng minh:MN là phân giác của góc KMH
e)Chứng minh:Ba điểm B,M,N thẳng hàng g)Chứng minh:BN ⊥ AD,BN ⊥ EC
h) Δ ABC thỏa mãn điều kiện gì để Δ NAD là tam giác đều
Cho △ABC vuông tại A. Tia phân giác của góc B cắt AC tại điểm M. Kẻ MD ⊥ BC (D ∈ BC).
a) Chứng minh rằng △ABM = △DBM.
b) Gọi E là giao điểm của 2 đường thẳng DM và BA. Chứng minh ME = MC.
c) Kẻ BH ⊥ EC tại H. Chứng minh rằng △ABC = △DBE và 3 điểm B, M, H thẳng hàng.
a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó: ΔBAM=ΔBDM
b: ΔBAM=ΔBDM
=>BA=BD và MA=MD
Xét ΔMAE vuông tại A và ΔMDC vuông tại D có
MA=MD
\(\widehat{AME}=\widehat{DMC}\)
Do đó: ΔMAE=ΔMDC
=>ME=MC
c: ΔMAE=ΔMDC
=>AE=DC
BA+AE=BE
BD+DC=BC
mà BA=BD
và AE=DC
nên BE=BC
Xét ΔABC vuông tại A và ΔDBE vuông tại D có
BC=BE
BA=BD
Do đó: ΔABC=ΔDBE
Ta có: BE=BC
=>B nằm trên đường trung trực của EC(1)
Ta có: ME=MC
=>M nằm trên đường trung trực của EC(2)
Xét ΔBEC có BE=BC
nên ΔBEC cân tại B
Ta có: ΔBEC cân tại B
mà BH là đường cao
nên BH là trung trực của EC(3)
Từ (1),(2),(3) suy ra B,M,H thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ MD⊥BC (D thuộc BC)
a) Chứng minh BA = BD.
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh △ABC = △DBE
c) Kẻ DH ⊥ MC ( H∈MC) và AK ⊥ ME ( K∈ME). Gọi N là giao điểm của DH và AK. Chứng minh MN là tia phân giác của góc HMK.
d) Chứng minh ba điểm B, M, N thẳng hàng.

nếu bạn ko thấy ảnh thì zô thống kê hỏi đáp của mình là thấy bài này nhá . ( cậu tìm câu nào có câu này r ấn zô xem nha )
hoặc link bài của mình nè
https://scontent-hkt1-1.xx.fbcdn.net/v/t1.15752-9/89947717_345887062999332_7304147707155709952_n.jpg?_nc_cat=110&_nc_sid=b96e70&_nc_ohc=Hj57duZ44dcAX91P2ra&_nc_ht=scontent-hkt1-1.xx&oh=7ea184f17776bd230198145c38f92aae&oe=5E95F1D5
Dễ vãi nồi
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ MD vuông góc với BC( D thuộc BC)
a) Chứng minh BA = BD
b) Gọi E là giao điểm của hai đường thẳng d m và B Chứng minh tam giác ABC bằng tam giác DBE.
c) kẻ BH vuông góc MC(H thuộc MC) và AK vuông góc vs ME. Chứng minh MN là tia phân giác góc HMK.
d) Chứng minh ba điểm B, M, N thẳng hàng
Hình tự vẽ
a, \(\Delta BAM\)và \(\Delta BDM\)có
\(\widehat{ABM}=\widehat{DBM}\left(gt\right)\)
\(AM\): cạnh chung
\(\widehat{BAM}=\widehat{BDM}\left(=90^o\right)\)
\(\Rightarrow\Delta BAM=\Delta BDM\left(ch-gn\right)\)
\(\Rightarrow BA=BD\)(2 cạnh tương ứng )
Để nghĩ tiếp :(
Đúng 0
Bình luận (0)
Ta có:
∠AMB+∠ABM=90o
∠BMD+∠MBD=900
Mà ∠AMB=∠BMD (gt)
=> ∠ABM=∠MBD
Xét ΔBAM và ΔBAM có:
∠ABM=∠MBD (gt)
BM chung
∠ABM=∠MBD (cmt)
=> ΔBAM = ΔBAM (g-c-g)
=> BA=BD (2 cạnh tương ứng)
b,Xét ΔABC và ΔDBE có:
∠ABC chung
∠BAC=∠BDM=90o
BA=BD (cmt)
=> ΔABC = ΔDBE (g-c-g)
c,Ta có
BC⊥ED
AK⊥ED
=> BC//AK hay BC//AN
=> ∠ANM=∠MBC ( 2 góc slt) (1)
Mà:
DH⊥AC
BA⊥AC
=> BA//DH hay BA//DN
=> ∠MND=∠ABM ( 2 góc so le trong) (2)
Mà ∠ABM=∠MBD ( vì BM là tia phân giác của góc ABC)
Từ(1) và (2) =>∠ANM=∠MND
=> NM là tia phân giác của góc HMK
d,Ta có BM là tia phân giác của góc ABC (3)
Và NM là tia phân giác của góc HMK
Vì ∠ANM=∠MBC
∠MND=∠ABM
=> ∠ANM=∠MBC=∠MND=∠ABM
=> BN là tia phân giác của góc ABC (4)
Từ (3) và (4) => B,M,N thẳng hàng
odfgjpodfpofsgpsf