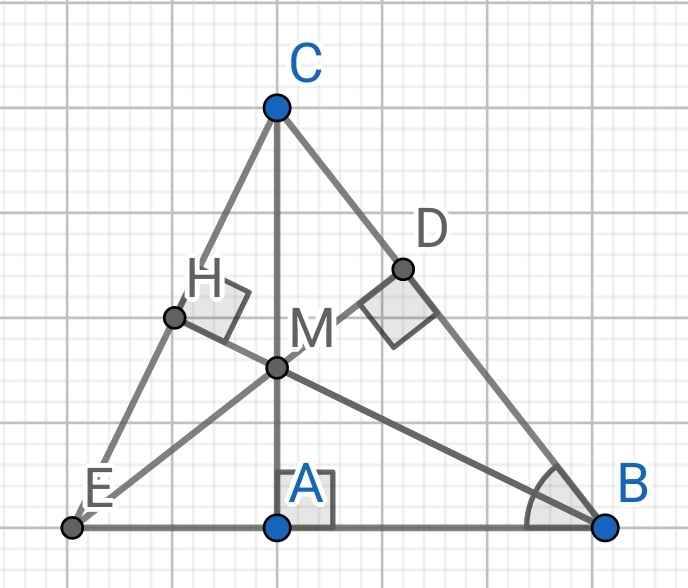
 a) Do BM là tia phân giác của ABC (gt)
a) Do BM là tia phân giác của ABC (gt)
⇒ ∠ABM = ∠DBM
Xét hai tam giác vuông: ∆ABM và ∆DBM có:
BM là cạnh chung
∠ABM = ∠DBM (cmt)
⇒ ∆ABM = ∆DBM (cạnh huyền - góc nhọn)
⇒ BA = BD (hai cạnh tương ứng)
b) Xét hai tam giác vuông: ∆ABC và ∆DBE có:
BA = BD (cmt)
∠B chung
⇒ ∆ABC = ∆DBE (cạnh huyền - góc nhọn)
c) Do ∠ABM = ∠DBM (cmt)
⇒ ∠EBM = ∠CBM
Do ∆ABC = ∆DBE (cmt)
⇒ BC = BE (hai cạnh tương ứng)
Xét ∆MBE và ∆MBC có:
BE = BC (cmt)
∠EBM = ∠CBM (cmt)
BM là cạnh chung
⇒ ∆MBE = ∆MBC (c-g-c)
⇒ ME = MC (hai cạnh tương ứng)
c) ∆BCE có:
CA ⊥ AB (ABC vuông tại A)
⇒ CA ⊥ BE
⇒ CA là đường cao của ∆BCE (1)
MD ⊥ BC (gt)
⇒ ED ⊥ BC
⇒ ED là đường cao thứ hai của ∆BCE (2)
M là giao điểm của AC và ED
⇒ M là giao điểm của ba đường cao của ∆BCE
Mà BH ⊥ CE (gt)
⇒ BH là đường cao thứ ba của ∆BCE
⇒ B, M, H thẳng hàng











