viết tắt của tập hợp số hữu tỉ là gì
N,Z,O,R
Cho số hữu tỉ x=\(\dfrac{a-20}{-3}\), gọi S là tập hợp tất cả các số nguyên dương của a để x là một số hữu tỉ dương.
a) Viết tập hợp S theo 2 cách.
b) Tính số tập con có 2 phần tử từ tập S.
Mik cần gấp nhé Cảm ơn![]()
![]()
![]()
Biểu đồ minh họa trong hình nói gì về quan hệ giữa tập hợp các số nguyên Z và tập hợp các số hữu tỉ Q ? Có thể nói mỗi số nguyên là một số hữu tỉ hay không?
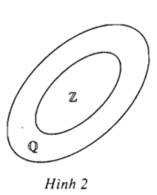
Tập hợp các số nguyên Z nằm trong tập hợp các số hữu tỉ Q
Có thể nói mỗi số nguyên là một số hữu tỉ
1. Tập hợp số tự nhiên, kí hiệu N
N={0, 1, 2, 3, ..}.
2. Tập hợp số nguyên, kí hiệu là Z
Z={…, -3, -2, -1, 0, 1, 2, 3, …}.
Tập hợp số nguyên gồm các phân tử là số tự nhiên và các phân tử đối của các số tự nhiên.
Tập hợp các số nguyên dương kí hiệu là N*
3. Tập hợp số hữu tỉ, kí hiệu là Q
Q={ a/b; a, b∈Z, b≠0}
Mỗi số hữu tỉ có thể biểu diễn bằng một số thập phân hữu hạn hoặc vô hạn tuần hoàn.
4. Tập hợp số thực, kí hiệu là R
Một số được biểu diễn bằng một số thập phân vô hạn không tuần hoàn được gọi là một số vô tỉ. Tập hợp các số vô tỉ kí hiệu là I. Tập hợp số thực gồm các số hữ tỉ và các số vô tỉ.
R = Q ∪ I.
5. Một số tập hợp con của tập hợp số thực.
+ Đoạn [a, b] ={x ∈ R / a ≤ x ≤ b}
+ Khoảng (a; b) ={x ∈ R / a < x < b}
– Nửa khoảng [a, b) = {x ∈ R / a ≤ x < b}
– Nửa khoảng (a, b] ={x ∈ R / a < x ≤ b}
– Nửa khoảng [a; +∞) = {x ∈ R/ x ≥ a}
– Nửa khoảng (-∞; a] = {x ∈ R / x ≤a}
– Khoảng (a; +∞) = {x ∈ R / x >a}
– Khoảng (-∞; a) = {x ∈R/ x<a}.
Luyện trắc nghiệmTrao đổi bàiCho số hữu tỉ x = \(\frac{a-20}{-3}\), gọi S là tập hợp tất cả các số nguyên dương của a để x là 1 số hữu tỉ dương.
a) Viết tập hợp S theo 2 cách
b) Tính số tập hợp con có 2 phần tử từ tập S.
Để \(x=\frac{a-20}{-3}\) ( a ∈ N* ) nhận giá trị dương
=> a - 20 nhận giá trị âm
=> a nhỏ hơn 20
a) S = { a ∈ N* | a < 20 }
\(S=\left\{...;17;18;19\right\}\)
b) ( Không hiểu đề , thông cảm , bạn làm nốt nhé ! )
uuuuuuuuuuuuuuuuuuuuuuuuuuuuu
Câu b)
Số tập hợp con có 2 phần tử từ tập S là
\(C^2_{17}=171\)(tập hợp con)
VẬY....
tập hợp Q các số hữu tỉ
số \(\dfrac{-25}{5}\)
a,là số tự nhiên (∈ N)
b,là số nguyên (∈ Z)
c, là số hữu tỉ (∈ Q)
chọn tất cả đáp án đúng
\(b,c\)\(\left(-\dfrac{25}{5}=-5\in Z\in Q\right)\)
Cho tập hợp A có CtHH R³O² biết tỉ lệ khối lượng của R và O là 7:3 (A) nguyên tố R là nguyên tố nào ?? (B) viết CTHH của hợp chất A
Các mệnh đề sau đúng hay sai?
a) Mọi số nguyên đều viết được dưới dạng phân số
b) Tập hợp các số thực chứa tập hợp các số hữu tỉ;
c) Tồn tại một số thực không là số hữu tỉ.
a) Mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.
Vì \(\forall a \in \mathbb{Z}:a = \dfrac{a}{1}\)
Hoặc: \(a \in \mathbb{Z} \subset \mathbb{Q}\) => mỗi số nguyên cũng là một phân số.
b) Mệnh đề "Tập hợp các số thực chứa tập hợp các số hữu tỉ" là mệnh đề đúng.
c) Mệnh đề “Tồn tại một số thực không là số hữu tỉ” đúng.
Ví dụ: \(\sqrt 2 \) ( vì \(\sqrt 2 \in \mathbb{R};\;\sqrt 2 \notin \mathbb{Q}\)).
1. Cho các số hữu tỉ .
a/ Hãy so sánh các số hữu tỉ đó .
b/ Viết tập hợp các số hữu tỉ bằng các số hữu tỉ trên .
Bài 1: Tập hợp số hữu tỉ được kí hiệu là?
A. N B. N* C. Q D. R