Cho (a+b)2=2(a2+b2).Chứng minh a=b
Những câu hỏi liên quan
10 tháng 1 2022 lúc 10:13
Câu 29. Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).Câu 30. Cho a3 + b3 2. Chứng minh rằng a + b ≤ 2.Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].Câu 32. Tìm giá trị lớn nhất của biểu thức: Câu 33. Tìm giá trị nhỏ nhất của: với x, y, z 0.Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:a) ab và a/b là số vô tỉ.b) a + b và a/b là số hữu tỉ (a + b ≠ 0)c) a + b, a2 và b2 là số hữu tỉ (a + b ≠...
Đọc tiếp
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].
Câu 32. Tìm giá trị lớn nhất của biểu thức: 
Câu 33. Tìm giá trị nhỏ nhất của: 
với x, y, z > 0.
Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:
a) ab và a/b là số vô tỉ.
b) a + b và a/b là số hữu tỉ (a + b ≠ 0)
c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)
Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 38. Cho a, b, c, d > 0. Chứng minh:
Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1
Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa:
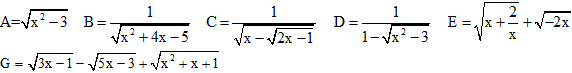Mn giúp em với ;-;
Cho hai số thực dương a và b thỏa mãn a + b ≤ 2.
Chứng minh a2/a2 + b2/b2 + a ≤ 1
Sửa đề : \(\dfrac{a^2}{a^2+b}+\dfrac{b^2}{b^2+a}\le1\\ \) (*)
\(< =>\dfrac{a^2\left(b^2+a\right)+b^2\left(a^2+b\right)}{\left(a^2+b\right)\left(b^2+a\right)}\le1\\ < =>a^2b^2+a^3+b^2a^2+b^3\le\left(a^2+b\right)\left(b^2+a\right)\) ( Nhân cả 2 vế cho `(a^{2}+b)(b^{2}+a)>0` )
\(< =>a^3+b^3+2a^2b^2\le a^2b^2+b^3+a^3+ab\\ < =>a^2b^2\le ab\\ < =>ab\le1\) ( Chia 2 vế cho `ab>0` )
Do a,b >0
Nên áp dụng BDT Cô Si :
\(2\ge a+b\ge2\sqrt{ab}< =>\sqrt{ab}\le1\\ < =>ab\le1\)
Do đó (*) luôn đúng
Vậy ta chứng minh đc bài toán
Dấu "=" xảy ra khi : \(a=b>0,a+b=2< =>a=b=1\)
Đúng 1
Bình luận (0)
a Sửa đề : Chứng minh \(\dfrac{a^2}{a^2+b}\)+\(\dfrac{b^2}{b^2+a}\)\(\le\) 1 ( Đề thi vào 10 Hà Nội).
Bất đẳng thức trên tương đương :
\(\dfrac{a^2+b-b}{a^2+b}\)+\(\dfrac{b^2+a-a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\) 1 - \(\dfrac{b}{a^2+b}\)+ 1 - \(\dfrac{a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\)1 - \(\dfrac{b}{a^2+b}\) - \(\dfrac{a}{b^2+a}\)\(\le\)0
\(\Leftrightarrow\)- \(\dfrac{b}{a^2+b}\)- \(\dfrac{a}{b^2+a}\)\(\le\)-1
\(\Leftrightarrow\)\(\dfrac{a}{b^2+a}\)+ \(\dfrac{b}{a^2+b}\)\(\ge\)1
Xét VT = \(\dfrac{a^2}{ab^2+a^2}\)+ \(\dfrac{b^2}{a^2b+b^2}\)\(\ge\)\(\dfrac{\left(a+b\right)^2}{ab^2+a^2+a^2b+b^2}\) (Cauchy - Schwarz)
= \(\dfrac{\left(a+b\right)^2}{ab\left(b+a\right)+a^2+b^2}\)
\(\ge\)\(\dfrac{\left(a+b\right)^2}{2ab+a^2+b^2}\)
= \(\dfrac{\left(a+b\right)^2}{\left(a+b\right)^2}\)= 1
Vậy BĐT được chứng minh
Dấu '=' xảy ra \(\Leftrightarrow\)a = b = 1
Đúng 0
Bình luận (0)
Cho z a + bi . Chứng minh rằng:a)
z
2
+
(
z
)
2
2(
a
2
−
b
2
)b)
z
2
−
(
z
)
2
4abic) ...
Đọc tiếp
Cho z = a + bi . Chứng minh rằng:
a) z 2 + ( z ) 2 = 2( a 2 − b 2 )
b) z 2 − ( z ) 2 = 4abi
c) z 2 . = ( a 2 + b 2 ) 2
z 2 = ( a + b i ) 2 = a 2 − b 2 + 2abi
( z ) 2 = ( a - b i ) 2 = a 2 − b 2 − 2abi
z.z− = (a + bi)(a − bi) = a 2 + b 2
Từ đó suy ra các kết quả.
Đúng 0
Bình luận (0)
Chứng minh rằng: (a + b)( a 2 – ab + b 2 ) + (a – b)( a 2 + ab + b 2 ) = 2 a 3
Biến đổi vế trái ta có:
VT = (a + b)( a 2 – ab + b 2 ) + (a – b)( a 2 + ab + b 2 )
= a 3 + b 3 + a 3 – b 3 = 2 a 3 = VP
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Đúng 0
Bình luận (0)
cho (a+b)2=2(a2+b2) chứng minh rằng a=b
Ta có: \(2\left(a^2+b^2\right)=\left(a+b\right)^2\)
\(\Leftrightarrow2a^2+2b^2-a^2-2ab-b^2=0\)
\(\Leftrightarrow a^2-2ab+b^2=0\)
\(\Leftrightarrow\left(a-b\right)^2=0\)
\(\Leftrightarrow a-b=0\)
hay a=b
Đúng 2
Bình luận (0)
Cho a,b,c không âm. Chứng minh rằng :
a) a2 + b2 + c2 + 2abc + 2 > hoặc=ab +bc +ca +a+b+c
b)a2 + b2 +c2 +abc +4 > hoặc = 2(ab+bc+ca)
c) 3(a2 + b2 + c2) + abc +4 > hoặc =4 (ab+bc+ca)
d) 3(a2 + b2 + c2) + abc +80 > 4(ab+bc+ca) + 8(a+b+c)
Ngu kkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
1 Cho biểu thức M a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.2 Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Đọc tiếp
1 Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
2 Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
Đúng 0
Bình luận (0)
chứng minh các đẳng thức sau
(a-b)2=a2-2ab+b2
(a-b)(a+b)=a2-b2
(a+b)3=a3+3a2b+3ab2+b3
(a-b)^2=(a-b)(a-b)=a^2-ab-ab+b^2=a^2-2ba+b^2
(a-b)(a+b)=a^2+ab-ab-b^2=a^2-b^2
(a+3)^3=(a+b)^2*(a+b)
=(a^2+2ab+b^2)(a+b)
=a^3+a^2b+2a^2b+2ab^2+b^2a+b^3
=a^3+3a^2b+3ab^2+b^3
Đúng 1
Bình luận (0)
\(Chứng minh các bất đẳng thức: a) (a + b)2 ≤ 2(a2 + b2) b) (a + b + c)2 ≤ 3(a2 + b2 + c2)\)
a)Ta có:
\(\left(a+b\right)^2+\left(a-b\right)^2=2\left(a^2+b^2\right)\)
Do \(\left(a-b\right)^2\ge0\),nên\(\left(a+b\right)^2\le2\left(a^2+b^2\right)\)
b)Xét \(\left(a+b+c\right)^2+\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2\)
Khai triển và rút gọn ta được:\(3\left(a^2+b^2+c^2\right)\)
Vậy \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\)
Đúng 0
Bình luận (0)