phân tích thành nhân tử:
a) x^6 - 64
b) (x + y)^3 + (x - y)^3
c) (x + y)^3 - (x - y)^3
Phân tích đa thức sau thành nhân tử:
a) (xy +1)^2 - (x-y)^2
b) (x + y)^3 - (x - y)^3
c) 3x^4y^2 + 3x^3y^2 + 3xy^2 + 3y^2
a, \(=\left(xy+1+x-y\right)\left(xy+1-x+y\right)\)
b, \(\left(x+y-x+y\right)[\left(x+y\right)^2+\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2]\)
\(=2y[x^2+2xy+y^2+x^2-y^2+x^2-2xy+y^2]\)
\(=2y\left(3x^2+y^2\right)\)
c,\(=3\left(x+1\right)^2\left(x^2-x+1\right)y^2\)
câu a, b áp dụng hằng đẳng thức rồi làm nha
c) 3x4y2 + 3x3y2 + 3xy2 + 3y2
= ( 3x4y2 + 3x3y2 ) + ( 3xy2 + 3y2 )
= 3x3y2 ( x + 1) + 3y2 ( x + 1 )
= ( 3x3y2 + 3y2 ) ( x + 1 )
= 3y2 ( x3 + 1 ) ( x + 1 )
= 3y2 ( x + 1 ) ( x2 - x + 1 ) ( x + 1 )
= 3y2 ( x + 1 )2 ( x2 - x + 1 )
a) (xy +1)2- (x-y)2
=(xy +1-x+y)(xy+1+x-y)
b) (x + y)3 - (x - y)3
= (x+y-x+y)((x+y)2+(x+y)(x-y)+(x - y)2)
= 2y(x2+2xy+y2+x2+xy-xy-y2+x2-2xy+y2)
=2y(3x2+y2)
c) 3x4y2 + 3x3y2 + 3xy2 + 3y2
=3y2(x4+x3+x+1)
= 3y2(x3(x+1)+(x+1)
= 3y2(x+1)(x3+1)
ko bt đúng ko
Phân tích các đa thức sau thành nhân tử:
a) \(8{x^3} - 1\)
b) \({x^3} + 27{y^3}\)
c) \({x^3} - {y^6}\)
`a, 8x^3 - 1 = (2x-1)(4x^2 + 2x - 1)`
`b, x^3 + 27y^3 = (x+3y)(x^3 - 3xy + 9y^2)`
`c, x^3 - y^6 = (x-y^2)(x+xy^2 + y^4)`
1A. Phân tích các đa thức sau thành nhân tử:
a) x3+2x; b) 3x - 6y;
c) 5(x + 3y)- 15x(x + 3y); d) 3(x-y)- 5x(y-x).
1B. Phân tích các đa thức sau thành nhân tử:
a) 4x2 - 6x; b) x3y - 2x2y2 + 5xy;
![]()
![]() c) 2x2(x +1) + 4x(x +1); d) 2 x(y - 1) - 2
c) 2x2(x +1) + 4x(x +1); d) 2 x(y - 1) - 2
y(1 - y).
5 5
2A. Phân tích các đa thức sau thành nhân tử: a) 2(x -1)3 - 5(x -1)2 - (x - 1);
b) x(y - x)3 - y(x - y)2 + xy(x - y);
c) xy(x + y)- 2x - 2y;
d) x(x + y)2 - y(x + y)2 + y2 (x - y).
2B. Phân tích đa thức thành nhân tử: a) 4(2-x)2 + xy - 2y;
b) x(x- y)3 - y(y - x)2 - y2(x - y);
c) x2y-xy2 - 3x + 3y;
d) x(x + y)2 - y(x + y) 2 + xy - x 2 .
1A:
a: \(x^3+2x=x\left(x^2+2\right)\)
b: \(3x-6y=3\left(x-2y\right)\)
c: \(5\left(x+3y\right)-15x\left(x+3y\right)\)
\(=5\left(x+3y\right)\left(1-3x\right)\)
d: \(3\left(x-y\right)-5x\left(y-x\right)\)
\(=3\left(x-y\right)+5x\left(x-y\right)\)
\(=\left(x-y\right)\left(5x+3\right)\)
1A. a. x(x2+2)
b. 3(x-2y)
c. 5(x+3y)(1-3x)
d. (x-y) (3-5x)
1B. a. 2x(2x-3)
b.xy(x2-2xy+5)
c. 2x(x+1)(x+2)
d. 2x(y-1)+2y(y-1)=2(y-1)(x-y)
1B:
a: \(4x^2-6x=2x\left(2x-3\right)\)
b: \(x^3y-2x^2y^2+5xy\)
\(=xy\left(x^2-2xy+5\right)\)
Bài 1: Phân tích đa thức thành nhân tử:
a) 3(x-y)^2+9y(y-x)^2
b) 3(x-y)^2+9y(y-x)
giúp e với ạ, em cảm ơn
a) \(3\left(x-y\right)^2+9y\left(y-x\right)^2\)
\(=3\left(x-y\right)^2+9y\left(x-y\right)^2\)
\(=\left(x-y\right)^2\left(3-9y\right)\)
\(=3\left(x-y\right)^2\left(3y+1\right)\)
b) \(3\left(x-y\right)^2+9y\left(y-x\right)\)
\(=3\left(y-x\right)^2+9y\left(y-x\right)\)
\(=\left(y-x\right)\left[3\left(y-x\right)+9y\right]\)
\(=3\left(y-x\right)\left(y-x+3y\right)\)
\(=3\left(y-x\right)\left(4y-x\right)\)
a: =3(x-y)^2+9y(x-y)^2
=(x-y)^2(3+9y)
=(x-y)^2*3*(y+3)
b: =3(x-y)^2-9y(x-y)
=3(x-y)(x-y-9y)
=3(x-y)(x-10y)
Phân tích các đa thức sau thành nhân tử:
a) \(P = 6x - 2{x^3}\)
b) \(Q = 5{x^3} - 15{x^2}y\)
c) \(R = 3{x^3}{y^3} - 6x{y^3}z + xy\)
`a, P = 2x(3 - x^2)`
`b, Q = 5x^2(x-3y)`
`c, R = xy(3x^2y^2 - 6y^2z + 1)`
a) \(P=6x-2x^3\)
\(P=2x\left(3+x^2\right)\)
b) \(Q=5x^3-15x^2y\)
\(Q=5x^2\left(x-3y\right)\)
c) \(R=3x^3y^3-6xy^3z+xy\)
\(R=xy\left(3x^2y^2-6y^2z+1\right)\)
a,P=2x(3−x2)𝑎,𝑃=2𝑥(3-𝑥2)
b,Q=5x2(x−3y)𝑏,𝑄=5𝑥2(𝑥-3𝑦)
c,R=xy(3x2y2−6y2z+1)
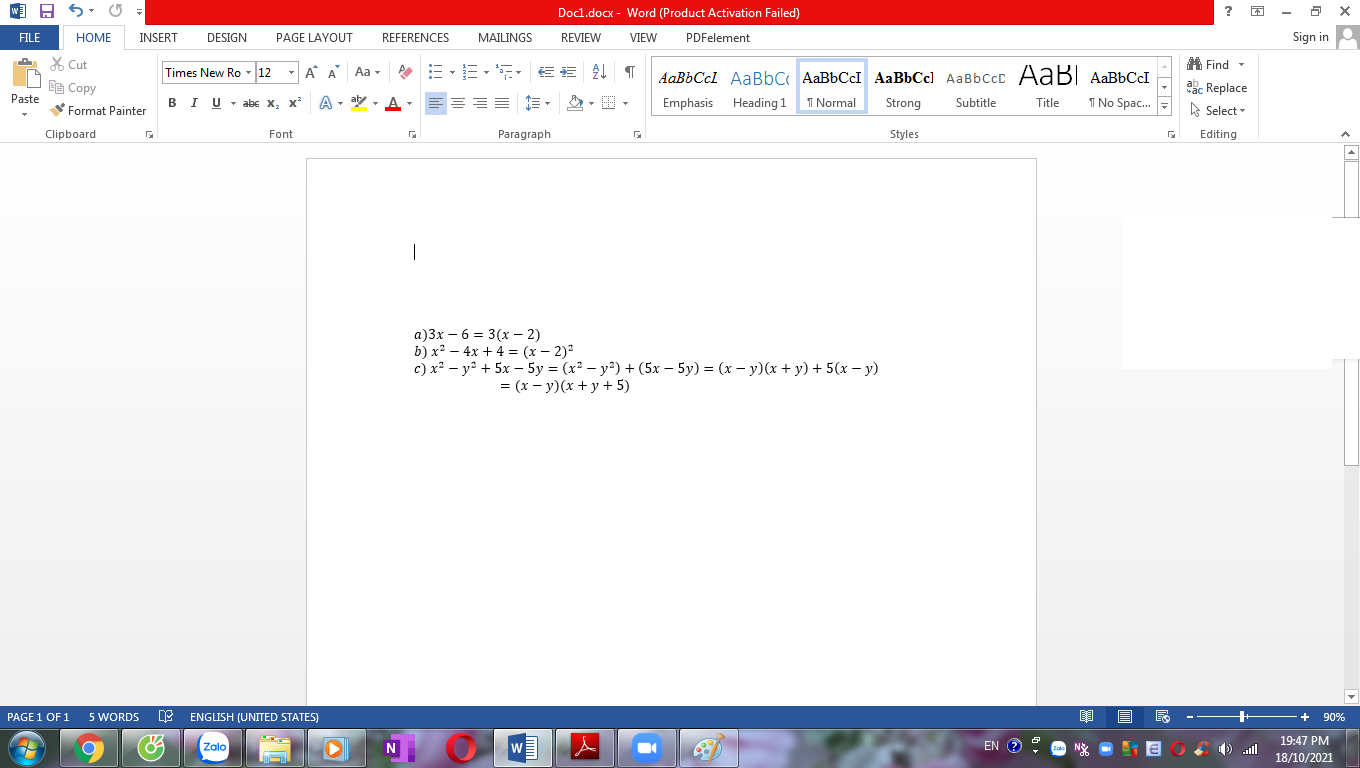
Phân tích các đa thức sau thành nhân tử:
a) 3x-6
b) x2-4x+4
c) x2-y2+5x-5y
d) 8(x+y+z)3-(x+y)3-(y+z)3-(y+z)3-(z+x)3
Do câu d mình ko biết làm bởi v mình không làm được
Phân tích các đa thức sau thành nhân tử:
a) \(4{x^3} - 16x\)
b) \({x^4} - {y^4}\)
c) \(x{y^2} + {x^2}y + \dfrac{1}{4}{y^3}\)
d) \({x^2} + 2x - {y^2} + 1\)
`a, 4x^3 - 16x = 4x(x^2-4) = 4x(x-2)(x+2)`
`b, x^4 - y^4 = (x^2-y^2)(x^2+y^2) = (x-y)(x+y)(x^2+y^2)`
`c, xy^2 + x^2y + 1/4y^3`
`= y(xy + x^2 + 1/4y^2)`
`d, x^2 + 2x - y^2 + 1 = (x+1)^2 - y^2`
`= (x+1+y)(x+1-y)`
phân tích đa thức sau thành nhân tử:
a)x^4-y^4
b)x^2-3y^2
c)(3x-2y)^2-4(x+y)^2
d)9(x-y)^2-4(x+y)^2
f)x^3+27
g)27x^3-0,001
h)125x^3-1
\(a,=\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\\ b,=\left(x-\sqrt{3}y\right)\left(x+\sqrt{3}y\right)\\ c,=\left[3x-2y-2\left(x+y\right)\right]\left[3x-2y+2\left(x+y\right)\right]\\ =5x\left(x-4y\right)\\ d,=\left[3\left(x-y\right)-2\left(x+y\right)\right]\left[3\left(x-y\right)+2\left(x+y\right)\right]\\ =\left(3x-3y-2x-2y\right)\left(3x-3y+2x+2y\right)\\ =\left(x-5y\right)\left(5x-y\right)\\ f,=\left(x+3\right)\left(x^2-3x+9\right)\\ g,=\left(3x-0,1\right)\left(9x^2+0,3x+0,01\right)\\ h,=\left(5x-1\right)\left(25x^2+5x+1\right)\)
\(a)x^4-y^4=(x^2-y^2)(x^2+y^2)=(x-y)(x+y)(x^2+y^2)\\ b)x^2-3y^2=\\ c)(3x-2y)^2-4(x+y)^2=(3x-2y)^2-[2(x+y)]^2\\=(3x-2y+2x+2y)(3x-2y-2x-2y)=5x(x-4y)\\ d)9(x-y)^2-4(x+y)^2=[3(x-y)]^2-[2(x+y)]^2=(3x-3y+2x+2y)(3x-3y-2x-2y)\\=(5x-y)(x-5y)\\ f)x^3+27=(x+3)(x^2-3x+9)\\ g)27x^3-0,001=(3x-0,1)(9x+0,3x+0,01)\\ h)125x^3-1=(5x-1)(25x^2+5x+1)\)
Phân tích các đa thức sau thành nhân tử:
a) 2(x -1)^ 3 - 5(x -1)^ 2 - (x - 1);
b) x(y - x)^ 3 - y(x - y)^ 2 + xy(x - y);
c) xy(x + y)- 2x - 2y;
d) x(x + y) ^2 - y(x + y)^ 2 + y^ 2 (x - y).
a: Ta có: \(2\left(x-1\right)^3-5\left(x-1\right)^2-\left(x-1\right)\)
\(=\left(x-1\right)\left[2\left(x-1\right)^2-5\left(x-1\right)-1\right]\)
\(=\left(x-1\right)\left(2x^2-4x+2-5x+5-1\right)\)
\(=\left(x-1\right)\left(2x^2-9x+6\right)\)
b: Ta có: \(x\left(y-x\right)^3-y\left(x-y\right)^2+xy\left(x-y\right)\)
\(=-x\left(x-y\right)^3-y\left(x-y\right)^2+xy\left(x-y\right)\)
\(=\left(x-y\right)\left[-x\left(x-y\right)^2-y\left(x-y\right)+xy\right]\)
\(=\left(x-y\right)\left[-x^3+2x^2y-xy^2-xy+y^2+xy\right]\)
\(=\left(x-y\right)\left(-x^3+2x^2y-xy^2+y^2\right)\)
a) \(2\left(x-1\right)^3-5\left(x-1\right)^2-\left(x-1\right)=\left(x-1\right)\left[2\left(x-1\right)^2-5\left(x-1\right)-1\right]=\left(x-1\right)\left(2x^2-4x+2-5x+5-1\right)=\left(x-1\right)\left(2x^2-9x+6\right)\)
b) \(x\left(y-x\right)^3-y\left(x-y\right)^2+xy\left(x-y\right)=\left(x-y\right)\left[-x\left(x-y\right)^2-y\left(x-y\right)+xy\right]=\left(x-y\right)\left(-x^3+2x^2y-xy^2-xy+y^2+xy\right)=\left(x-y\right)\left(-x^3+y^2+2x^2y-xy^2\right)\)
c) \(xy\left(x+y\right)-2x-2y=xy\left(x+y\right)-2\left(x+y\right)=\left(x+y\right)\left(xy-2\right)\)
d) \(x\left(x+y\right)^2-y\left(x+y\right)^2+y^2\left(x-y\right)=\left(x+y\right)^2\left(x-y\right)+y^2\left(x-y\right)=\left(x-y\right)\left(x^2+2xy+y^2+y^2\right)=\left(x-y\right)\left(x^2+2y^2+2xy\right)\)
\(a.2\left(x-1\right)^3-5\left(x-1\right)^2-\left(x-1\right)\\ =\left(x-1\right)\left[2\left(x-1\right)^2-5\left(x-1\right)-1\right]\\ =\left(x-1\right)\left(2x^2-9x+6\right)\)
Phân tích các đa thức sau thành nhân tử:
a)6x^2y
b)x^2(x-y)+4(y-x)
c)x^3+2x^2y+xy^2-4x
a: 6x-2y=2(3x-y)
b: =(x-y)(x-2)(x+2)
Lời giải:
a. Không phân tích được nữa
b. $x^2(x-y)+4(y-x)=x^2(x-y)-4(x-y)=(x-y)(x^2-4)=(x-y)(x-2)(x+2)$
c. $x^3+2x^2y+xy^2-4x=x(x^2+2xy+y^2-4)$
$=x[(x^2+2xy+y^2)-4]=x[(x+y)^2-2^2]=x(x+y-2)(x+y+2)$
ko phân tích dc
b: =(x-y)(x-2)(x+2)