GIẢI PHƯƠNG TRÌNH:
(X+5)4+(X-4)4=(2X+1)4.
giải phương trình (x+5)^4+(x-4)^4=(2x+1)^4
Đặt \(\hept{\begin{cases}x+5=a\\x-4=b\end{cases}\Rightarrow2x+1=a+b}\)
\(\left(x+5\right)^4+\left(x-4\right)^4=\left(2x+1\right)^4\)
\(\Rightarrow a^4+b^4=\left(a+b\right)^4\)
\(\Rightarrow a^4+b^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4\)
\(\Rightarrow4a^3b+6a^2b^2+4ab^3=0\)
\(\Rightarrow4ab\left[a^2+\frac{3}{2}ab+b^2\right]=0\)(1)
Mà \(a^2+\frac{3}{2}ab+b^2=\left(a+\frac{3}{4}b\right)^2+\frac{7}{16}b^2>0\)(2)
(vì nếu a và b đồng thời bằng 0 thì x + 5 và x - 4 đồng thời = 0 điều đó vô lý)
Từ (1) và (2), ta được
\(\orbr{\begin{cases}a=0\\b=0\end{cases}\Rightarrow}\orbr{\begin{cases}x+5=0\\x-4=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-5\\x=4\end{cases}}}\)
Chúc bạn học tốt.
Giải các phương trình sau a) 5-(x-6)=4(3-2x); b) 3 - x ( 1 - 3x)=5(1-2x); c) (x-3)(x+4)-2(3x-2)= (x-4)²
`5-(x-6)=4(3-2x)`
`<=>5-x+6-4(3-2x)=0`
`<=> 5-x+6-12 +8x=0`
`<=> 7x -1=0`
`<=> 7x=1`
`<=>x=1/7`
Vậy pt đã cho có nghiệm `x=1/7`
__
`3-x(1-3x) =5(1-2x)`
`<=> 3-x+3x^2=5-10x`
`<=> 3-x+3x^2-5+10x=0`
`<=> 3x^2 +9x-2=0`
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-9+\sqrt{105}}{6}\\x=\dfrac{-9-\sqrt{105}}{6}\end{matrix}\right.\)
Vậy pt đã cho có tập nghiệm \(S=\left\{\dfrac{-9+\sqrt{105}}{6};\dfrac{-9-\sqrt{106}}{5}\right\}\)
__
`(x-3)(x+4) -2(3x-2)=(x-4)^2`
`<=>x^2+4x-3x-12- 6x +4 =x^2 -8x+16`
`<=>x^2-5x-8=x^2-8x+16`
`<=> x^2 -5x-8-x^2+8x-16=0`
`<=> 3x-24=0`
`<=>3x=24`
`<=>x=8`
Vậy pt đã cho có nghiệm `x=8`
a) 5-(x-6)=4(3-2x)
=> 5 – x + 6 = 12 – 8x
=> -x + 8x = 12 – 5 – 6
=> 7x = 1
=> x=1/7
Vậy phương trình có nghiệm x=1/7
b) 3 - x ( 1 - 3x)=5(1-2x)
=> 3-x+3x^2=5-10x
=> 3x^2+9x-2= 0
0=105
=> x =\(\dfrac{-9-\sqrt{105}}{6}\)
Giải phương trình và bất phương trình:
a ) 9 x 2 - 4 = x - 1 x + 2 + 3 x - 2 b ) x - 5 = 2 x c ) x - 2 2 + 2 x - 1 ≤ x 2 + 4
a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2
(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)
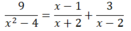
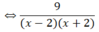
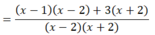
![]()
![]()
Vậy tập nghiệm của pt là: S = {-1; 1}
b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0
Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x
⇔ x = -5 hoặc x = 5/3
Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}
c) x – 2)2 + 2(x – 1) ≤ x2 + 4
⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4
⇔ -2x ≤ 2
⇔ x ≥ -1
Tập nghiệm S = {x | x ≥ -1}
Giải bất phương trình
a) 4(x-3)2-(2x-1)2<10
b) x(x-5)(x+5)-(x+2)(x2-2x+4)<hoặc= 3
a: =>4x^2-24x+36-4x^2+4x-1<10
=>-20x<10-35=-25
=>x>=5/4
b: =>x(x^2-25)-x^3-8<=3
=>x^3-25x-x^3-8<=3
=>-25x<=11
=>x>=-11/25
Giải phương trình:
\(\dfrac{2x+1}{x^2-5x+4}+\dfrac{5}{x-1}=\dfrac{2}{x-4}\)
ĐKXĐ: ` x ne 1 ; x ne 4`
`(2x+1)/(x^2-5x+4) + 5/(x-1) = 2/(x-4)`
`<=> (2x+1)/[(x-1)(x-4)] + [5(x-4)]/[(x-1)(x-4)] = [2(x-1)]/[(x-1)(x-4)]`
`=> 2x+1 + 5x -20 = 2x-2`
`<=> 5x = 17`
`<=> x= 17/5`(thỏa mãn ĐKXĐ)
Vậy tập nghiệm của phương trình là `S={ 17/5}`
giải các phương trình sau :
1,(2x+5)(x-4) = (x-5)(4-x)
2,9x^2-1 = (3x+1)
1) \(\left(2x+5\right)\left(x-4\right)=\left(x-5\right)\left(4-x\right)\)
\(\Leftrightarrow\left(2x+5\right)\left(x-4\right)+\left(x-4\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-4\right)\cdot3x=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=0\end{cases}}\)
2) \(9x^2-1=3x+1\)
\(\Leftrightarrow\left(3x+1\right)\left(3x-1\right)-\left(3x+1\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{3}\\x=\frac{2}{3}\end{cases}}\)
Giải các bất phương trình sau
a) 4(x-3)2-(2x-1)2<10
b) x(x-5)(x+5)-(x+2)(x2-2x+4)< hoặc = 3
\(a,4\left(x-3\right)^2-\left(2x-1\right)^2< 10\)
\(\Leftrightarrow4\left(x^2-6x+9\right)-\left(4x^2-4x+1\right)-10< 0\)
\(\Leftrightarrow4x^2-24x+36-4x^2+4x-1-10< 0\)
\(\Leftrightarrow-20x< -25\)
\(\Leftrightarrow x>\dfrac{5}{4}\)
\(b,x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)\le3\)
\(\Leftrightarrow x\left(x^2-25\right)-\left(x^3-2x^2+4x+2x^2-4x+8\right)\le3\)
\(\Leftrightarrow x^3-25x-\left(x^3+8\right)\le3\)
\(\Leftrightarrow x^3-25x-x^3-8-3\le0\)
\(\Leftrightarrow-25x\le11\)
\(\Leftrightarrow x\ge-\dfrac{11}{25}\)
Giải phương trình:
a,/2x-5/-/x-4/=4x
b,/2x-1/+/2x-5/=4
| x | \(\frac{5}{2}\) | 4 | |||
| 2x-5 | - | 0 | + | | | + |
| x-4 | - | | | - | 0 | + |
+) Nếu \(x\le\frac{5}{2}\Leftrightarrow\left|2x-5\right|=5-2x\)
\(\left|x-4\right|=4-x\)
\(pt\Leftrightarrow5-2x-4+x=4x\)
\(\Leftrightarrow-5x=-1\)
\(\Leftrightarrow x=\frac{1}{5}\left(tm\right)\)
+) Nếu \(\frac{5}{2}< x\le4\Leftrightarrow\left|2x-5\right|=2x-5\)
\(\left|x-4\right|=4-x\)
\(pt\Leftrightarrow2x-5-4+x=4x\)
\(\Leftrightarrow-x=9\)
\(\Leftrightarrow x=-9\) (loại)
+) Nếu \(x>4\Leftrightarrow\left|2x-5\right|=2x-5\)
\(\left|x-4\right|=x-4\)
\(pt\Leftrightarrow2x-5-x+4=4x\)
\(\Leftrightarrow-3x=1\)
\(\Leftrightarrow x=-\frac{1}{3}\)( loại )
Vậy ...
( p/s : câu b tương tự )
giải phương trình: 1/x + 5/2x+3 = 3/2x+1 + 4/x+3
Lời giải:
ĐKXĐ: $x\neq 0; \frac{-3}{2}; \frac{-1}{2}; -3$
PT $\Leftrightarrow (\frac{1}{x}-\frac{3}{2x+1})+(\frac{5}{2x+3}-\frac{4}{x+3})=0$
$\Leftrightarrow \frac{1-x}{x(2x+1)}+\frac{3-3x}{(2x+3)(x+3)}=0$
$\Leftrightarrow \frac{1-x}{x(2x+1)}+\frac{3(1-x)}{(2x+3)(x+3)}=0$
$\Leftrightarrow (1-x)\left[\frac{1}{x(2x+1)}+\frac{3}{(2x+3)(x+3)}\right]=0$
TH1: $1-x=0\Leftrightarrow x=1$ (tm)
TH2: $\frac{1}{x(2x+1)}+\frac{3}{(2x+3)(x+3)}=0$
$\Rightarrow (2x+3)(x+3)+3x(2x+1)=0$
$\Leftrightarrow 8x^2+12x+9=0$
$\Leftrightarrow (2x+3)^2+4x^2=0$
$\Rightarrow (2x+3)^2=x^2=0$ (vô lý)
Do đó $x=1$ là nghiệm duy nhất.