\(cosA+cosB+cosC=2cos\left(\dfrac{A+B}{2}\right)cos\left(\dfrac{A-B}{2}\right)+1-2sin^2\dfrac{C}{2}\)

\(=-2sin^2\dfrac{C}{2}+2sin\dfrac{C}{2}cos\left(\dfrac{A-B}{2}\right)+1\)

\(=-2\left[sin\dfrac{C}{2}-\dfrac{1}{2}cos\dfrac{A-B}{2}\right]^2-\dfrac{1}{2}sin^2\dfrac{A-B}{2}+\dfrac{3}{2}\le\dfrac{3}{2}\)

bn ni đi sưu tầm link đc đó

bn ni lừa ta à

Ta có \(a^4+b^4\ge2a^2.b^2\) (Bất đẳng thức Cô si với \(a^2;b^2\ge0\) )
Tương tự \(b^4+c^4\ge2b^2.c^2;a^4+c^4\ge2a^2.c^2\)
Do đó: \(a^4+b^4+c^4\ge\dfrac{2a^2b^2+2b^2c^2+2a^2c^2}{2}=a^2b^2+b^2c^2+a^2c^2\)(1)
Ta lại có:\(a^2b^2+b^2c^2\ge2ab^2c;b^2c^2+a^2c^2\ge2abc^2;a^2c^2+a^2b^2\ge2a^2bc\)
Nên\(a^2b^2+b^2c^2+a^2c^2\ge a^2bc+ab^2c+abc^2=abc\left(a+b+c\right)=3abc\left(a+b+c=3,gt\right)\)
(1);(2) => \(a^4+b^4+c^4\ge3abc\) ;đẳng thức xảy ra khi a = b = c = 1 (*)
Giả sử: \(a^3+b^3+c^3\ge3abc\\ \Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\ge0\\ \Leftrightarrow\left(a+b+c\right)^3-3ab\left(a+b+c\right)-3c\left(a+b\right)\left(a+b+c\right)\ge0\\ \Leftrightarrow\left(a+b+c\right)\left[\left(a+b+c\right)^2-ab-bc-ac\right]\ge0\\2.3\left(a^2+b^2+c^2-ab-bc-ac\right)\ge0\\ \Leftrightarrow3\left(2a^2+2b^2+2c^2-2ab-2bc-2ac\right)\ge0\\\Leftrightarrow3\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\right]\ge0\)
Đúng mới mọi a,b,c ϵR 
Vậy \(a^3+b^3+c^3\ge3abc\) và đẳng thức xảy ra khi a=b=c=(a+b+c)/3 =1(**)
Ta lại có \(a^4\ge a^3;b^4\ge b^3;c^4\ge c^3\) mà a+b+c = 3
Nên \(a^4+b^4+c^4>a^3+b^3+c^3\) (***)
Từ (*);(**);(***) ta có điều phải chứng minh và đẳng thức xảy ra khi a= b=c=1
 

Tôi có cách chứng minh bằng đồng bậc hóa bất đẳng thức như sau:

ta sẽ chứng minh:

\(3\left(a^4+b^4+c^4\right)>=\left(a+b+c\right)\left(a^3+b^3+c^3\right)\)
<=> \(2\left(a^4+b^4+c^4\right)>=ab\left(a^2+b^2\right)+bc\left(b^2+c^2\right)+ca\left(c^2+a^2\right)\)

mà ta có theo bất đẳng thức AMGM \(a^4+b^4>=\dfrac{\left(a^2+b^2\right)^2}{2}>=\dfrac{2ab\left(a^2+b^2\right)}{2}=ab\left(a^2+b^2\right)\)
làm tương tự rồi cộng lại, ta có đpcm.

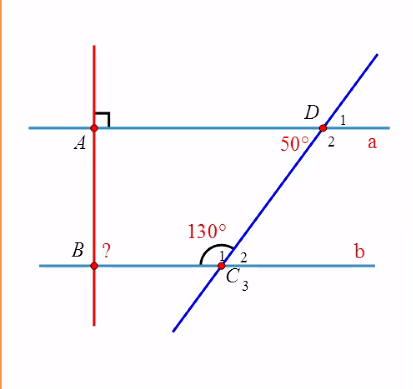
a) Ta có: \(\widehat{ADC}+\widehat{C_1}=50^0+130^0=180^0\)

Mà 2 góc này là 2 trong cùng phía

=> a//b

b) Ta có: a//b,a⊥AB

=> b⊥AB=> \(\widehat{B}=90^0\)

Ta có: a//b

\(\Rightarrow\widehat{D_2}=\widehat{C_1}=130^0\)(so le trong)

Ta có: \(\widehat{C_3}=\widehat{C_1}=130^0\)(đối đỉnh)

Ta có: \(\widehat{D_1}=\widehat{ADC}=50^0\)(đối đỉnh)

Ta có: a//b

\(\Rightarrow\widehat{C_2}=\widehat{ADC}=50^0\)(so le trong)

1. AVERAGE(a,b,c,...)

SUM(a,b,c,...)

MIN(a,b,c,...)

MAX(a,b,c,...)

2. a).(-18-2)^2-(7+6)^3

b). (24^3/3-5^2)*9

c). (10*X+3)^3/6*X^2+2

d). A*X^3+B*X^2+C*X+D

3. Các ô đó sẽ hiện ra kết quả của C3+E5

Đúng thì tick nha!!! ^^

Đề thiếu rồi bạn

C

C

C. A3,A4,B3,B4,C3 và C4. 

1: Ta có: \(a^2+b^2+c^2\)

\(=\left(a+b+c\right)^2-2\cdot\left(ab+bc+ca\right)\)

\(=5^2-2\cdot174=-323\)