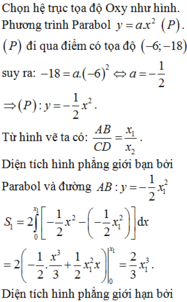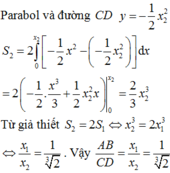Hãy tự thiết kế một cổng chào hình parabol.

Những câu hỏi liên quan
Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.
Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
Gọi phương trình của parabol là \({y^2} = 2px\)
Ta có chiều cao của cổng \(OH = BK = 10\), chiều rộng tại chân cổng \(BD = 2BH = 5\)
Vậy điểm B có tọa độ là \(B\left( {10;\frac{5}{2}} \right)\)
Thay tọa độ điểm B vào phương trình parabol ta có:
\({\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}\), suy ra phương trình parabol có dạng \({y^2} = \frac{5}{8}x\)
Thay \(x = 2\) vào phương trình \({y^2} = \frac{5}{8}x\) ta tìm được \(y = \frac{{\sqrt 5 }}{2}\)
Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là \(\sqrt 5 \) m
Đúng 0
Bình luận (0)
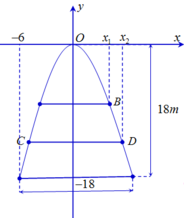
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽbên). Tỉ số
A
B
C
D
bằng : A.
1
2
B.
4
5...
Đọc tiếp
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽbên). Tỉ số A B C D bằng :

A. 1 2
B. 4 5
C. 1 2 3
D. 3 1 + 2 2
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽbên). Tỉ số
A
B
C
D
bằng : A.
1
2
B.
4
5
C...
Đọc tiếp
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽbên). Tỉ số A B C D bằng :
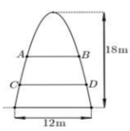
A. 1 2
B. 4 5
C. 1 2 3
D. 3 1 + 2 2
Đáp án C
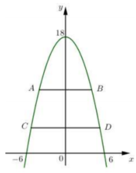


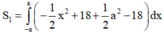



Diện tích hình phẳng giới hạn bởi parabol và đường thẳng CD là:

= − c 3 6 + c 3 2 − c 3 6 − c 3 2 = 2 c 3 3 S 1 = 2 3 S ⇒ 2 3 c 3 = 2 3 .144 = 96 ⇒ c = 2 18 3 ⇒ C D = 2 c ⇒ 4 18 3 ⇒ A B C D = 1 2 3
Đúng 0
Bình luận (0)
Cổng chào của một thành phố có dạng hình parabol có khoảng cách giữa hai chân cổng là 4,5 m. Từ một điểm M trên thân cổng, người ta đo được khoảng cách từ điểm đó đến mặt đất(điểm H)là 1,8 m và khoảng cách từ điểm H đến chân cổng gần nhất là 1 m. Tính chiều cao của cổng theo đơn vị mét,làm tròn tới hàng phần mười.
Xem chi tiết
Một cổng chào có dạng hình Parabol chiều cao18m, chiều rộng chân đế12m. Người ta căng hai sợi dây trang trí AB, CDnằm ngang đồng thời chia hình giới hạn bởi Parabol và mặt đất thành ba phần có diện tích bằng nhau . Tỉ số AB/CD bằng A.
3
1
+
2
2
B.
1
2...
Đọc tiếp
Một cổng chào có dạng hình Parabol chiều cao18m, chiều rộng chân đế12m. Người ta căng hai sợi dây trang trí AB, CDnằm ngang đồng thời chia hình giới hạn bởi Parabol và mặt đất thành ba phần có diện tích bằng nhau . Tỉ số AB/CD bằng
A. 3 1 + 2 2
B. 1 2
C. 4/5.
D. 1 2 3
Cổng chào một trung tâm triển lãm có dạng parabol y = - x^2/20 , biết chiều cao h = 5 m. Tìm chiều dài d của cổng.
Xem chi tiết
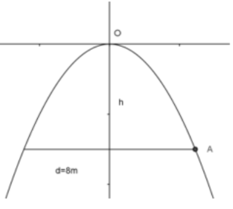
Một chiếc cổng hình parabol dạng y = - x 2 / 2 có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (h.25).
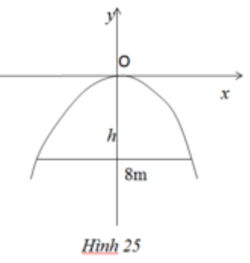
Thiết kế một chóa đèn có mặt cắt hình parabol với kích thước được cho trong hình sau:

Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng \({y^2} = 2px\)
Gắn hệ tọa độ Oxy vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ (3; 9)
Thay tọa độ điểm (3; 9) vào phương trình \({y^2} = 2px\), ta có \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
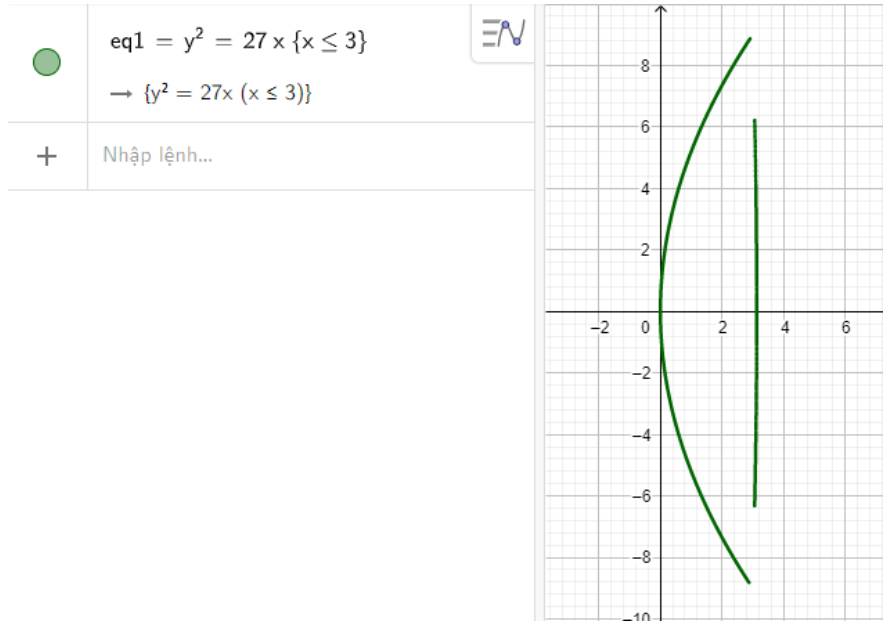
Suy ra phương trình mô tả chóa đèn là \({y^2} = 27x\) với \(x \le 3\)
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới:
Đúng 0
Bình luận (0)
1) Một chiếc cổng hình parabol gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao của cổng parabol là 4M còn kích thước ở giữa là 3M✖4M. Hãy tính khoảng cách giửa hai điểm A và B.