Các câu hỏi tương tự
Biết rằng parabol
y
1
24
x
2
chia hình phẳng giới hạn bởi elip có phương trình
x
2
16
+
y
2
1
1
thành hai phần có diện tích lần lượt là S1,S2với S1S2. Tỉ số của
S
1
S...
Đọc tiếp
Biết rằng parabol y = 1 24 x 2 chia hình phẳng giới hạn bởi elip có phương trình x 2 16 + y 2 1 = 1 thành hai phần có diện tích lần lượt là S1,S2với S1<S2. Tỉ số của S 1 S 2 bằng
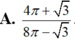
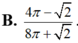
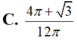

Gọi (H) là hình phẳng giới hạn bởi parabol y
(
x
-
3
)
2
trục hoành và trục tung. Gọi k1,k2(k1k2) lần lượt là hệ số góc của đường thẳng qua điểm A(0;9 và chia (H) thành ba hình mặt phẳng có diện tích bằng nhau( tham khảo hình vẽ bên). Giá trị của k1-k2 bằng
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi parabol
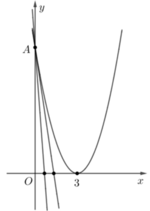
y= ( x - 3 ) 2 trục hoành và trục tung. Gọi k1,k2(k1>k2) lần lượt là hệ số góc của đường thẳng qua điểm A(0;9 và chia (H) thành ba hình mặt phẳng có diện tích bằng nhau( tham khảo hình vẽ bên). Giá trị của k1-k2 bằng

![]()
![]()
Gọi (H) là hình phẳng giới hạn bởi parabol (P)
y
8
x
-
x
2
và trục hoành. Các đường thẳng y a; y b;y c với 0abc16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức
16
-
a
3
+
16
-
b...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi parabol (P) y = 8 x - x 2 và trục hoành. Các đường thẳng y = a; y = b;y =c với 0<a<b<c<16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức 16 - a 3 + 16 - b 3 + 16 - c 3 bằng
A. 2048.
B. 3584.
C. 2816.
D. 3480.
Cho hàm số
y
x
3
+
a
x
2
+
b
x
+
c
có đồ thị (C) . Biết rằng tiếp tuyến d của (C) tại điểm A có hoành độ bằng -1 cắt (C) tại B có hoành độ bằng 2 (xem hình vẽ). Diện tích hình phẳng giới hạn bởi d và (C) (phần gạch chéo trong hình vẽ) bằng: A.
27
4
B.
11...
Đọc tiếp
Cho hàm số y = x 3 + a x 2 + b x + c có đồ thị (C) . Biết rằng tiếp tuyến d của (C) tại điểm A có hoành độ bằng -1 cắt (C) tại B có hoành độ bằng 2 (xem hình vẽ). Diện tích hình phẳng giới hạn bởi d và (C) (phần gạch chéo trong hình vẽ) bằng:
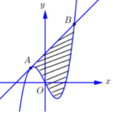
A. 27 4
B. 11 2
C. 25 4
D. 13 2
Biết rằng parabol
y
1
24
x
2
chia hình phẳng giới hạn bởi elip có phương trình
x
2
16
+
y
2
1
1
thành hai phần có diện tích lần lượt là
S
1
,
S...
Đọc tiếp
Biết rằng parabol
y
=
1
24
x
2
chia hình phẳng giới hạn bởi elip có phương trình
x
2
16
+
y
2
1
=
1
thành hai
phần có diện tích lần lượt là
S
1
,
S
2
với
S
1
<
S
2
. Tỉ số
S
1
S
2
bằng
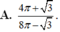
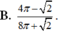
Cho đồ thị
(
C
)
:
y
ax
3
+
bx
2
+
cx
+
d
và Parabol
(
P
)
:
y
mx
2
+
nx
+
p
có đồ thị như hình vẽ (đồ thị (C) là đường cong đậm hơn). Biết phần hình phẳng được giới hạn bởi (C) và (P) (...
Đọc tiếp
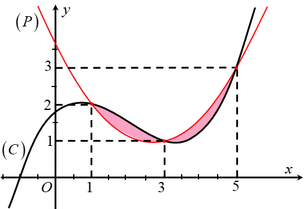
Cho đồ thị ( C ) : y = ax 3 + bx 2 + cx + d và Parabol ( P ) : y = mx 2 + nx + p có đồ thị như hình vẽ (đồ thị (C) là đường cong đậm hơn). Biết phần hình phẳng được giới hạn bởi (C) và (P) (phần tô đậm) có diện tích bằng 1. Thể tích của khối tròn xoay tạo thành khi quay phần hình phẳng đó quanh trục hoành bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Diện tích hình phẳng giới hạn bởi các đường x-1, x2, y0 và Parabol (P)
y
a
x
2
+
b
x
+
c
bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Khi đó a+b-c bằng bao nhiêu? A. -8 B. -2 C. 14 D. 3
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đường x=-1, x=2, y=0 và Parabol (P) y = a x 2 + b x + c bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Khi đó a+b-c bằng bao nhiêu?
A. -8
B. -2
C. 14
D. 3
Gọi (H) là hình phẳng giới hạn bởi parabol
y
x
-
3
2
, trục hoành và trục tung. Gọi
k
1
,
k
2
(
k
1
k
2
)
lần lượt là hệ số góc của các đường thẳng đi qua điểm A(0;9) và chia (H) t...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi parabol y = x - 3 2 , trục hoành và trục tung. Gọi k 1 , k 2 ( k 1 > k 2 ) lần lượt là hệ số góc của các đường thẳng đi qua điểm A(0;9) và chia (H) thành ba phần có diện tích bằng nhau (tham khảo hình vẽ bên).
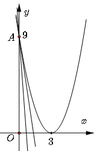
Giá trị của k 1 - k 2 bằng
A. ![]() .
.
B. 7.
C. ![]() .
.
D ![]() .
.
Người ta dự định trồng hoa Lan Ý để trang trí vào phần tô đậm (như hình vẽ). Biết rằng phần tô đậm là diện tích hình phẳng giới hạn bởi hai đồ thị
y
f
(
x
)
ax
3
+
bx
2
+...
Đọc tiếp
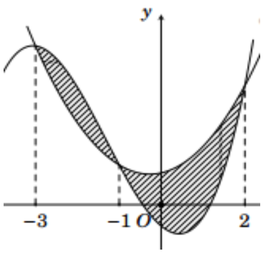
Người ta dự định trồng hoa Lan Ý để trang trí vào phần tô đậm (như hình vẽ). Biết rằng phần tô đậm là diện tích hình phẳng giới hạn bởi hai đồ thị y = f ( x ) = ax 3 + bx 2 + cx - 1 2 và y = g x = dx 2 + ex + 1 trong đó a , b , c , d , e ∈ ℝ Biết rằng hai đồ thị đó cắt nhau tại các điểm có hoành độ lần lượt bằng -3; -1; 2 chi phí trồng hoa là 800000 đồng/1m2 và đơn vị trên các trục được tính là 1 mét. Số tiền trồng hoa gần nhất với số nào sau đây? (làm tròn đến đơn vị nghìn đồng).
A. 4217000 đồng.
B. 2083000 đồng.
C. 422000 đồng.
D. 4220000 đồng.








