Trong mặt phẳng Oxy cho điểm \(S(x;y)\) di động trên đường thẳng \(d:12x - 5y + 16 = 0\). Tính khoảng cách ngắn nhất từ điểm \(M(5;10)\) đến điểm S.

Những câu hỏi liên quan
a) Tính khoảng cách từ gốc toạ độ C(0;0) đến điểm M(3 ; 4) trong mặt phẳng toạ độ Oxy.
b) Cho hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy. Nêu công thức tính độ dài đoạn thẳng IM.
a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)
Đúng 0
Bình luận (0)
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x(1,2), vecto y(3,4), vecto z(5,-1). Tọa độ vecto u 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4...
Đọc tiếp
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa độ vecto u = 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4,7). Tọa độ trung điểm I của đoạn thẳng MN là
6. Cho vecto x=(-4,7) và hai vecto a=(2,-1), b=(-3,4). Nếu vecto x = m vecto a + n vecto b thì m, n là cặp số nào
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với
M
0
;
10
,
N
100
;
10
và P(100;0). Gọi S là tập hợp tất cả các điểm
A
x
;
y
,
x
,
y...
Đọc tiếp
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M 0 ; 10 , N 100 ; 10 và P(100;0). Gọi S là tập hợp tất cả các điểm A x ; y , x , y ∈ ℤ nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm A x ; y ∈ S . Xác suất để x + y ≤ 90 bằng
A. 845 1111
B. 473 500
C. 169 200
D. 86 101
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;10), N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y), (x, y
∈
Z) nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm A(x;y)
∈
S. Xác suất để x + y
≤
90 bằng
Đọc tiếp
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;10), N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y), (x, y ∈ Z) nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm A(x;y) ∈ S. Xác suất để x + y ≤ 90 bằng
![]()
![]()
![]()
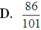
Điểm A(x;y) nằm bên trong (kể cả trên cạnh) của
![]()
Có 101 cách chọn x, 11 cách chọn y. Do đó số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là n( Ω ) = 101 x 11
Gọi X là biến cố: “Các điểm A(x;y) thỏa mãn x + y ≤ 90”.
Vì
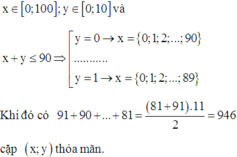
Vậy xác suất cần tính là
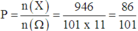
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ oxy cho hình vuông abcd biết đường thẳng delta: x-2y-3=0 và I(0,1) là giao điểm của hai đường chéo AC và BD . Tính S của hình vuông
Đường thẳng delta ở đây đóng vai trò là gì bạn?
Đúng 0
Bình luận (0)
1. Trong mặt phẳng Oxy, cho đường tròn (C): x^2+y^2-2x+4y-40và điểm M(-1;-3). Gọi I là tâm của (C). Viết phương trình đường thẳng đi qua M và cắt (C) tại hai điểm A,B sao cho tam giác IAB có diện tích lớn nhất2. Trong mặt phẳng Oxy, cho đường tròn (C): x^2+y^2+4x+4y-170 và điểm A(6;17). Viết phương trình tiếp tuyến của (C) biế tiếp tuyến đi qua điểm A.
Đọc tiếp
1. Trong mặt phẳng Oxy, cho đường tròn (C): \(x^2+y^2-2x+4y-4=0\)và điểm M(-1;-3). Gọi I là tâm của (C). Viết phương trình đường thẳng đi qua M và cắt (C) tại hai điểm A,B sao cho tam giác IAB có diện tích lớn nhất
2. Trong mặt phẳng Oxy, cho đường tròn (C): \(x^2+y^2+4x+4y-17=0\) và điểm A(6;17). Viết phương trình tiếp tuyến của (C) biế tiếp tuyến đi qua điểm A.
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với
M
0
;
1
;
0
,
N
100
;
10
và
P
100
;
0
.
Gọi S là tập hợp tất cả các điểm
A
x
;
y...
Đọc tiếp
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M 0 ; 1 ; 0 , N 100 ; 10 và P 100 ; 0 . Gọi S là tập hợp tất cả các điểm A x ; y với x , y ∈ ℤ nằm bên trong (kể cả trên cạnh) của OMNP . Lấy ngẫu nhiên một điểm A x ; y . Xác suất để x + y ≤ 90 bằng:
A. 845 1111 .
B. 473 500 .
C. 169 200 .
D. 86 101 .
Đáp án D.
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là n Ω = 101 × 11.
Vì x ∈ 0 ; 100 ; y ∈ 0 ; 10 và x + y ≤ 90
⇒ y = 0 → x = 0 ; 1 ; 2 ; ... ; 90 y = 1 → x = 0 ; 1 ; 2 ; ... ; 89 ... y = 10 → x = 0 ; 1 ; 2 ; ... ; 80 .
Khi đó có 91 + 90 + ... + 81 = 946 cặp x ; y thỏa mãn.
Vậy xác suất cần tính là:
P = n ( X ) n Ω = 946 101 × 11 = 86 101 .
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;1;0) ,N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y) với
x
,
y
∈
ℤ
nằm bên trong (kể cả trên cạnh) của OMNP . Lấy ngẫu nhiên một điểm A(x;y). Xác suất để
x
+
y
≤...
Đọc tiếp
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;1;0) ,N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y) với x , y ∈ ℤ nằm bên trong (kể cả trên cạnh) của OMNP . Lấy ngẫu nhiên một điểm A(x;y). Xác suất để x + y ≤ 90 bằng
A. 845 1111
B. 473 500
C. 169 200
D. 86 101
Đáp án D
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là
n Ω = 101 x 11
![]()
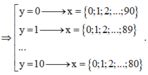
Khi đó có 91 + 90 + . . . + 81 = 946 cặp (x;y) thỏa mãn
Vậy xác suất cần tính là
![]()
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;10), N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y) với x,y ϵ ℤ nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm A(x;y)ϵS Xác suất để x+y ≤ 90 bằng: A. 845/1111 B. 473/500 C. 169/200 D. 86/101
Đọc tiếp
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;10), N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y) với x,y ϵ ℤ nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm A(x;y)ϵS Xác suất để x+y ≤ 90 bằng:
A. 845/1111
B. 473/500
C. 169/200
D. 86/101
Chọn đáp án D.
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là n(Ω)=101x11
Vì x ϵ [0;100];y ϵ [0;10] và x+y ≤90 ⇒ y = 0 → x = 0 ; 1 ; 2 ; . . . ; 90 y = 1 → x = 0 ; 1 ; 2 ; . . . ; 89 . . . y = 10 → x = 0 ; 1 ; 2 ; . . . ; 80
Khi đó có 91 + 90 + … + 81 = 946 cặp (x;y) thỏa mãn.
Vậy xác suất cần tính là P=n(X)/n(Ω)=86/101
Đúng 0
Bình luận (0)












